Trắc nghiệm Ôn tập chương 2 Giải tích 12 có đáp án có đáp án năm 2023 (phần 2)

---

Trắc nghiệm Ôn tập chương 2 Giải tích 12 có đáp án có đáp án năm 2023 (phần 2)

Với bộ Trắc nghiệm Ôn tập chương 2 Giải tích 12 có đáp án có đáp án năm 2023 (phần 2) sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Giải tích lớp 12.

Câu 1: Tìm các đường tiệm cận ngang của đồ thị hàm số

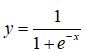
A. y = 0    C. y = 0 và y = 1

B. y = -1   D. y = 0 và y = -1

Hiển thị đáp án

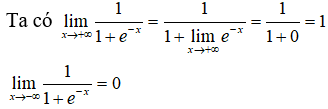
Từ đó suy ra hàm số có hai tiệm cận ngang là y = 1 và y = 0

Câu 2: Ngày 27 tháng 3 năm 2016 bà Mai gửi tiết kiệm vào ngân hàng số tiền 100 triệu đồng với hình thức lãi kép và lãi suất 6,8% một năm. Bà Mai dự tính đến ngày 27 tháng 3 năm 2020 thì rút hết tiền ra để lo công chuyện. Hỏi bà sẽ rút được bao nhiêu tiền (làm tròn kết quả đến hàng nghìn) ?

A. 38949000 đồng   C. 31259000 đồng

B. 21818000 đồng   D. 30102000 đồng

Hiển thị đáp án

Số tiền lãi bà Mai nhận được sau 4 năm (2020 - 2016 = 4 năm) là :

100000000(1 + 0,068)⁴ - 100000000 ≈ 30102000(đồng)

Câu 3: Tính đạo hàm của hàm số

Hiển thị đáp án

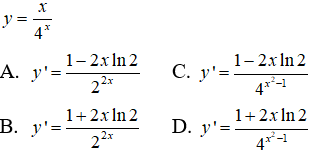
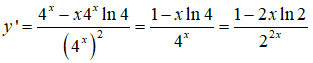
Câu 4: Cho hàm số

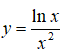
Khẳng định nào sau đây đúng ?

A. x = e² là điểm cực đại của hàm số

B. x = e² là điểm cực tiểu của hàm số

C. x = √e là điểm cực đại của hàm số

D. x = √e là điểm cực tiểu của hàm số

Hiển thị đáp án

Tập xác định: D = (0; +∞)

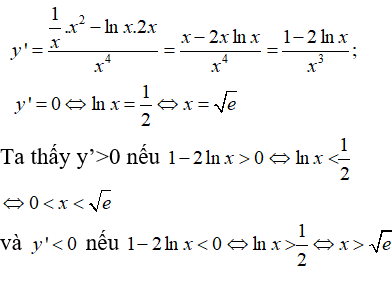
Nên x = √e là điểm cực đại của hàm số

Câu 5: Giải phương trình

Hiển thị đáp án

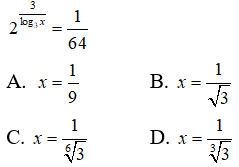
Điều kiện : log₃x ≠ 0 ⇔ x ≠ 1

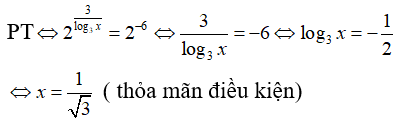
Câu 6: Tính tổng bình phương các nghiệm của phương trình 3^{2 + x} + 3^{2 - x} = 82

A. 4   B. 8   C. 12   D. 16

Hiển thị đáp án

Ta có:

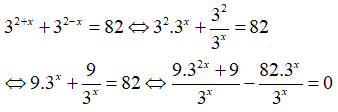
PT <⇒ 9.3^2x - 82.3^x + 9 = 0. Đặt t = 3^x (t > 0), nhận được phương trình

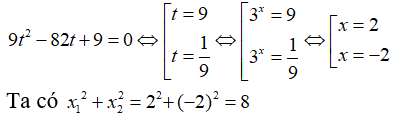
Câu 7: Nếu log_kx.log₅k = 3 thì x bằng

A. k³    B. k⁵    C. 125   D. 243

Hiển thị đáp án

Điều kiện: x > 0

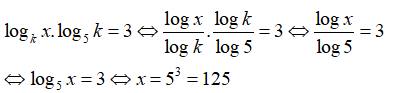
Câu 8: x là nghiệm của phương trình log₃x + log⁹x + log²⁷x = 11/2 . Hãy tính x^-1/3

A. x = 3    B. x = 1/3    C. x = ∛9   D. x = 1/∛9

Hiển thị đáp án

Điều kiện: x > 0

PT <⇒ log₃x + log₃2x + log₃3x = 11/2

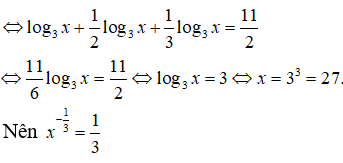
Câu 9: Giả sử x là nghiệm của phương trình 4^log₂x + x² = 8. Tính (log₃x)³

A. 1    B. 8   C. 2√2    D. ±1

Hiển thị đáp án

Điều kiện: x > 0

Ta có: 4^log₂x = 2^2log₂x = 2^log₂x2 = x².

Do đó phương trình đã cho tương đương với:

x² + x² = 8 ↔ 2x² = 8 <⇒ x² = 4 <⇒ x = 2 (do x > 0) .

Vậy (log₂x)³ = 1³ = 1

Câu 10: Giải bất phương trình 9^x - 82.3^x + 81 ≤ 0

A. 1 ≤ x ≤ 4    B. 0 ≤ x ≤ 4     C. 1 ≤ x ≤ 5    D. 0 ≤ x ≤ 5

Hiển thị đáp án

Đặt t = 3^x (t > 0), nhận được bất phương trình:

t² - 82t + 81 ≤ 0 <⇒ 1 ≤ t ≤ 81 <⇒ 1 = 3⁰ ≤ 3^x ≤ 3⁴ <⇒ 0 ≤ x ≤ 4

Câu 11: Khẳng định nào sau đây là đúng?

Hiển thị đáp án

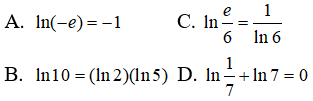
Câu 12: Lôgarit cơ số 3 của 27.∜9.∛9 là:

Hiển thị đáp án

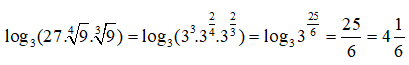
Câu 13: Tính giá trị biểu thức 7^log₇7 - log₇7⁷

A. 0   B. -6   C. 7   D. 1/7

Hiển thị đáp án

7^log₇7 - log₇7⁷ = 7 - 7log₇7 = 7 - 7.1 = 0

Câu 14: Giải phương trình 10^x = 400

A. x = 2log4   B. x = 4log2    C. x = 2log2 + 2   D. x = 4

Hiển thị đáp án

10^x = 400 ⇒ x = log400 = log(2².10²) = log2² + log10² = 2log2 + 2

Câu 15: Nếu logx - 5log3 = -2 thì x bằng

A. 0,8   B. 0,81   C. 1,25   D. 2,43

Hiển thị đáp án

Điều kiện: x > 0

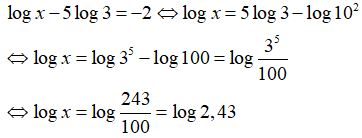
⇒ x = 2,43

Câu 16: Giải bất phương trình 2^x + 2^{x + 1} ≤ 3^x + 3^{x - 1}

A. x ≤ 2    B. x ≤ -2    C. x ≥ 2   D. x ≥ -2

Hiển thị đáp án

2^x + 2^{x + 1} ≤ 3^x + 3^{x - 1} <⇒2^x + 2.2^x ≤ 3^x + (1/3).3x^x <⇒ 3.2^x ≤ 4/3.3^x

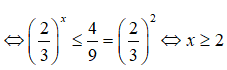
Câu 17: Giải bất phương trình log45x - log3 > 1

Hiển thị đáp án

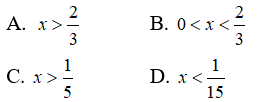
Điều kiện: x > 0

log45x - log3 > 1 <⇒ log(45x/3) > 1 <⇒ log15x > 1 <⇒ 15x > 10 <⇒ x > 2/3

Kết hợp điều kiện ta được: x > 2/3

Câu 18: Rút gọn biểu thức

Hiển thị đáp án

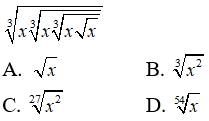
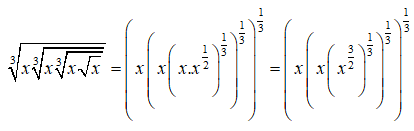
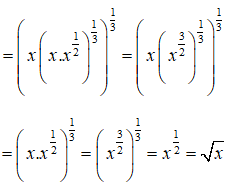
Câu 19: Tìm các điểm cực trị của hàm số

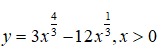
A.x = -1   B. x = 1    C. x = 1/2   D. x = 2

Hiển thị đáp án

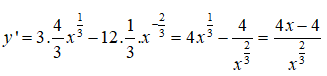
Ta thấy y’ đổi dấu khi đi qua điểm x = 1 nên hàm số có một điểm cực trị là x = 1.

Câu 20: Đặt log2 = a, log3 = b . Khi đó log₅12 bằng

Hiển thị đáp án

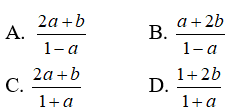
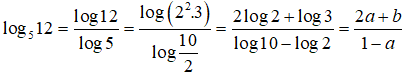
Câu 21: Cho N > 1 . Tìm số thực x thỏa mãn

Hiển thị đáp án

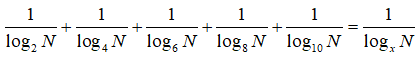
Phương trình đã cho tương đương với:

log_Nx = log_N2 + log_N4 + log_N6 + log_N8 + log_N10

⇔ log_Nx = log_N(2.4.6.8.10)

⇔ log_Nx = log_N3840

⇒ x = 3840

Câu 22: Cho a và b là hai số thực thỏa mãn 3^a = 81^{b + 2} và 125^b = 5^{a - 3} . Tính giá trị của ab

A. -60    B. -17   C. 12   D. 60

Hiển thị đáp án

Từ giả thiết có: 3^a = 3^{4(b + 2)} và 5^3b = 5^{a - 3}.

Từ đó suy ra: a = 4(b + 2) và 3b = a - 3.

giải hệ này tìm được a = -12, b = -5. Từ đó ab = 60

Câu 23: Ông A gửi tiết kiệm vào ngân hàng 200 triệu đồng với hình thức lãi kép. Sau 5 năm ông rút hết tiền ra được một khoản 283142000 đồng. Hỏi ông A gửi với lãi suất bao nhiêu, biết rằng trong thời gian đó lãi suất không thay đổi?

A. 6,8% một năm   C. 7,2% một năm

B. 7% một năm   D. 8% một năm

Hiển thị đáp án

Giả sử lãi suất là r.

Sau 5 năm ông rút hết tiền ra được một khoản là:

Ta có 200000000.(1 + r)⁵ = 283142000

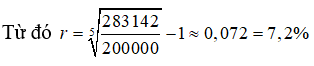
Câu 24: Số lượng cá thể của một mẻ cấy vi khuẩn sau t ngày kể từ lúc ban đầu được ước lượng bởi công thức N(t) = 1200.(1,48)^t . Sau bao lâu thì số lượng vi khuẩn đạt đến 5000 cá thể? Làm tròn kết quả đến hàng phần mười

A. 10,3 ngày   B. 12,3 ngày   C. 13,0 ngày   D. 61,7 ngày

Hiển thị đáp án

Số lượng vi khuẩn đạt đến 5000 cá thể khi 5000 = 1200.(1,148)^t

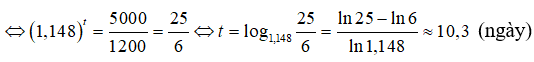
Câu 25: Tìm tập nghiệm của bất phương trình

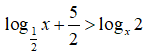
A. (0; 4)   C. (-∞; 1) ∪ (√2; 4)

B. (√2; 4)   D. (0; 1) ∪ (√2; 4)

Hiển thị đáp án

Điều kiện: x > 0

Ta có:

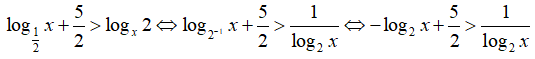
Đặt t = log₂x , nhận được bất phương trình

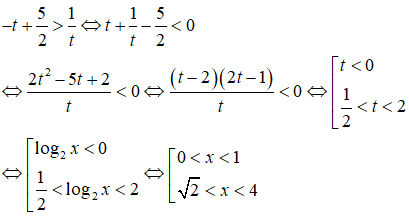
Câu 26: Trong các số được liệt kê trong bốn đáp án A, B, C, D dưới đây, số nào bé nhất?

Hiển thị đáp án

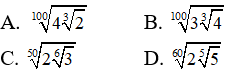
Viết các số hạng về cùng dạng căn bậc 300 của một biểu thức :

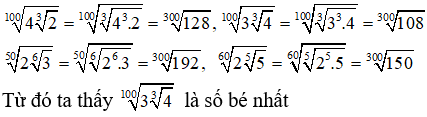
Câu 27: Tính giá trị biểu thức: P = log(tan1^o) + log(tan2^o) + log(tan3^o) +...+ log(tan88^o) + log(tan89^o)

Hiển thị đáp án

P = log(tan1^o.tan2^o.tan3^o...tan88^o.tan89^o )

= log((tan1^o.tan89^o).(tan2^o.tan88^o)...tan45^o)

= log(1.1...1) = log1 = 0

Câu 28: Cho p và q là các số dương thỏa mãn log₉p = log₁₂q = log₁₆(p + q) . Tính giá trị của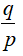

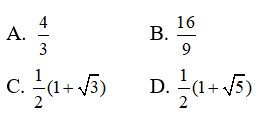
Hiển thị đáp án

Đặt log₉p = log₁₂q = log₁₆(p + q) = t

⇒ p = 9^t, q = 12^t, p + q = 16^t

⇒ 9^t + 12^t = 16^t hay 3^2t + 3^t.4^t = 4^2t

Chia cả hai vế đẳng thức này cho 3^2t ta được

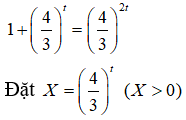
ta được: 1 + X = X²

X² - X - 1 = 0

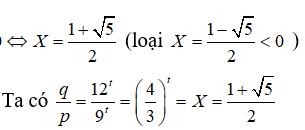
Câu 29: Gọi P và Q là hai điểm trên đồ thị hàm số y = e^x/2 lần lượt có hoành độ ln4 và ln16 . Kí hiệu l là độ dài đoạn thẳng PQ. Hệ thức nào sau đây đúng?

A. l² = 4(ln4 + 1)   C. l² = 4(ln16 + 1)

B. l² = 4((ln4)² + 1)   D. l² = 4((ln2)² + 1)

Hiển thị đáp án

Ta có:

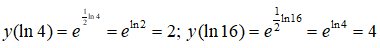
Do đó P(ln4; 2) và Q(ln16; 4)

Từ đó l² = (ln16 - ln4)² + (4 - 2)² = (ln4)² + 4 = (2ln2)² + 4 = 4((ln2)² + 1)

Câu 30: Giải bất phương trình 3^{2x + 1} - 2^{2x + 1} - 5.6^x ≤ 0

A. x ≤ 0    B. x ≥ 0    C. x ≤ log_3/22   D. x ≥ log_3/22

Hiển thị đáp án

Viết lại bất phương trình thành

3^{2x + 1} - 2^{2x + 1} - 5.6^x ≤ 0 ⇔ 3.3^2x - 2.2^2x - 5.2^x.3^x ≤ 0

Chia hai vế của bất phương trình cho 2^2x , ta được

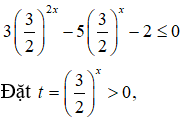
ta được bất phương trình: 3t² - 5t - 2 ≤ 0

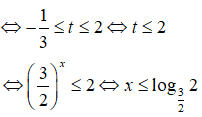
Câu 31: Giải bất phương trình log(x² - 2x - 2) ≤ 0

A. [-1; 3]    C. [-1; 1 - √3) ∪ (1 + √3; 3]

B. (1 - √3; 1 + √3)    D. (-∞; -1) ∪ (3; +∞)

Hiển thị đáp án

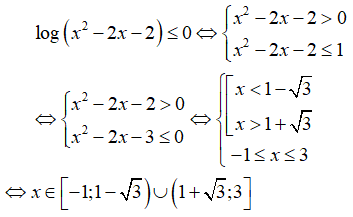
<⇒ x ∈ [-1; 1 - √3] ∪ (1 + √3; 3)

Câu 32: Tìm tập nghiệm của bất phương trình log_0,1(x² + x - 2) > log_0,1(x + 3)

A. (-√5; √5)    C. (-√5) ∪ (1; √5)

B. (-3; -√5) ∪ (√5; +∞)    D. (-√5; -2) ∪ (1; √5)

Hiển thị đáp án

Vì 0 < 0, 1 < 1 nên bất phương trình đã cho tương đương với

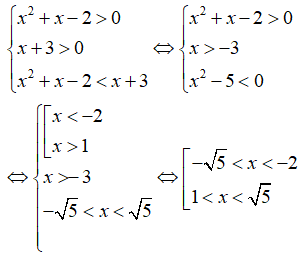
Câu 33: Tìm miền xác định của hàm số y = ln(ln(lnx))

A. D = (0; +∞)     B. D = (1; +∞)    C. D = (e; +∞)    D. D = (e^e; +∞)

Hiển thị đáp án

Điều kiện:

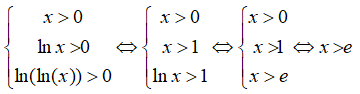
Câu 34: Tìm số x khác 0 thỏa mãn (7x)¹⁴ = (14x)⁷

A. 7   B. 14    C. 1/7    D. 2/7

Hiển thị đáp án

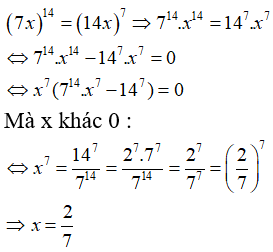
Câu 35: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Hiển thị đáp án

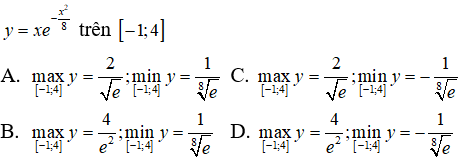
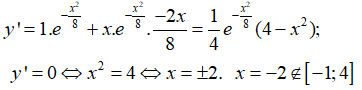
Ta có:

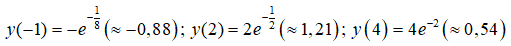
y(4) = 4^-2 (≈ 0,54)

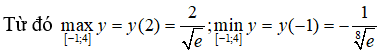
Câu 36: Số lượng của một đàn chim sau thời gian t tháng kể từ khi được quan sát được ước lượng bằng công thức

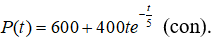
Sau bao lâu kể từ khi được quan sát thì đàn chim có số lượng đông nhất ?

A. 1 tháng    B. 4 tháng   C. 5 tháng    D. 8 tháng

Hiển thị đáp án

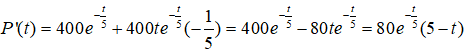
P'(t) = 0 <⇒ t = 5.

Bảng biến thiên

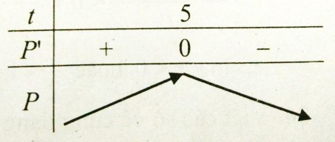
Từ đó ta thấy sau 5 tháng thì đàn chim đạt số lượng đông nhất

Câu 37: Tìm các giá trị x thỏa mãn

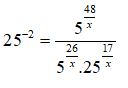
A. 2     B. 3    C. 5    D. 6

Hiển thị đáp án

Điều kiện: x ≠ 0

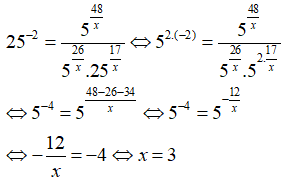
Câu 38: Giải phương trình 2^{x2 - 2x}.3^x = 3/2

A. x = 1, x = 1 - log₂3     C. x = 1, x = 1 + 2log₂3

B. x = 1, x = 1 + log₂3     D. x = 1, x = 1 - 2log₂3

Hiển thị đáp án

Lấy lôgarit cơ số 2 hai vế, ta được:

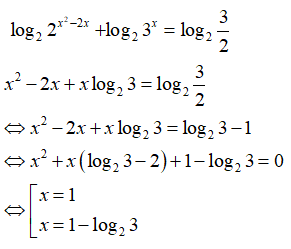
Câu 39: Cho phương trình log₅x + log₃x = log₅3.log₉225 . Phương trình nào sau đây không tương đương với phương trình đã cho?

A. log₅x + log₃5.log₅x = log₅3.log₃15

B. log₅x(1 + log₃5) = log₅3(1 + log₃5)

C. log₅x = log₃5

D. log₃x = 1

Hiển thị đáp án

Từ các phương án đã cho, ta nên biến đổi tương đương phương trình sao cho xuất hiện biểu thức log₅x như sau :

log₅x + log₃x = log₅3.log₉225 <⇒ log₅x + log₃5.log₅x = log₅3.log_2²15²

<⇒ log₅x + log₃5.log₅x = log₅3.log₃15 <⇒ log₅x(1 + log₃5) = log₅3(1 + log₃5)

<⇒ log₅x = log₅3 <⇒ x = 3

Từ đó ta thấy chỉ có phương trình log₅x = log₃5 là không tương đương với phương trình đã cho.

Nhận xét. Lưu ý rằng hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm. Như vậy một phương trình tương đường với phương trình đã cho thì không nhất thiết phải xuất hiện trong quá trình giải phương trình đã cho đó.