Trắc nghiệm Ôn tập chương 4 Giải tích 12 có đáp án có đáp án năm 2023
Trắc nghiệm Ôn tập chương 4 Giải tích 12 có đáp án có đáp án năm 2023
Với bộ Trắc nghiệm Ôn tập chương 4 Giải tích 12 có đáp án có đáp án năm 2023 sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Giải tích lớp 12.
Câu 1: Cho hai số phức z1 = 1 + 2i, z2 = 2 - 3i . Phần thực và phần ảo của số phức w = 3z1 - 2z2 là
A. 1 và 12 B. -1 và 12 C. –1 và 12i D. 1 và 12i.
Ta có: w = 3z1 - 2z2 = 3(1 + 2i) - 2(2 - 3i) = -1 + 2i.
Vậy phần thực và phần ảo của w là -1 và 12
Câu 2: Phần thực và phần ảo của số phức z = (1 + √3i)2 là
A. 1 và 3 B. 1 và -3 C. -2 và 2√3 D. 2 và -2√3 .
Ta có: z = 1 + 2√3 + 3i2 = -2 + 2√3i
Vậy phần thực và phần ảo của z là -2 và 2√3
Câu 3: Phần ảo của số phức z = (1 + √i)3 là
A. 3√3 B. -3√3 C. – 8i D. –8.
Ta có: z = i(1 + √3i)3 = i(1 + 3√3i - 9 - 3√3i) = -8i .
Vậy phần ảo của z là -8
Câu 4: Thực hiện phép tính:
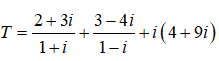
ta có:
A. T = 3 + 4i B. T = -3 + 4i C. T = 3 – 4i D. T = -3 – 4i.
Ta có:
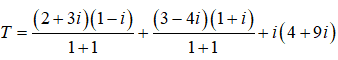
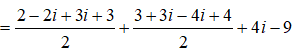
=> T = -3 + 4i
Câu 5: Môđun của số phức z thỏa mãn điều kiện z + (2 - i)z− = 13 - 3i là
A. 3 B. 5 C. 17 D. √17
Môđun của số phức z thỏa mãn điều kiện z + (2 - i)z− = 13 - 3i là:
Đặt z = a + bi(a, b ∈ R). Ta có: z− = a - bi và (2 - i)z− = (2 - i)(a - bi) = 2a - 2bi - ai - b = 2a - b - (2b + a)i
Do đó : z = (2 - i)z− = 13 - 3i ⇔ a + bi + 2a - b - (2b + a)i = 13 - 3i
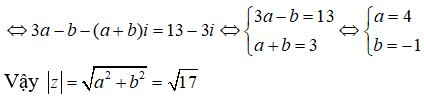
Câu 6: Phần thực và phần ảo của số phức z thỏa mãn (1 - i)z - 1 + 5i = 0 là
A. 3 và –2 B. 3 và 2 C. 3 và – 2i D. 3 và 2i.
Ta có: (1 - i)z - 1 + 5i = 0 ⇔ (1 - i)z = 1 - 5i
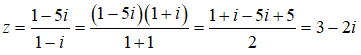
Vậy phần thực và phần ảo của z là 3 và -2
Câu 7: Môđun của số phức z thỏa mãn điều kiện (3z - z−)(1 + i) - 5z = 8i - 1 là
B. 1 B. 5 C. √13 D. 13.
Đặt z = a + bi(a, b ∈ R).
Ta có: z− = a - bi và 3z - z− = 3(a + bi) - (a - bi) = 2a + 4bi,
Do đó: (3z - z−)(1 + i) = 2a - 4b + (2a + 4b)i - 5(a + bi) = 8i - 1
Theo giả thiết: (2a - 4b) + (2a + 4b)i - 5(a + bi) = 8i - 1
⇔ -3a - 4b + (2a - b)i = -1 + 8i
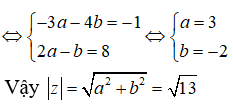
Câu 8: Cho số phức z thỏa mãn: i.z− + z = 2 + 2i và z.z− = 2. Khi đó z2 bằng:
A. 2 B. 4 C. – 2i D. 2i.
Đặt z = a + bi(a, b ∈ R). Ta có: z− = a - bi và z.z− = a2 + b2 = 2(1)
Ta có: i.z− + z = 2 + 2i ⇔ i(a - bi) + a + bi = 2 + 2i
⇔ a + b + (a + b)i = 2 + 2i ⇔ a + b = 2 (2)
Từ (1) và (2) suy ra a = b = 1. Suy ra z=1+i
Vậy z2 = (1 + i)2 = 1 + 2i - 1 = 2i
Câu 9: Cho số phức z thỏa mãn (1 + i)(z - i) + 2z = 2i. Môđun của số phức:
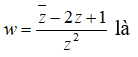
A. 2 B. 4 C. √10 D. 10
Đặt z = a + bi(a, b ∈ R). Ta có :
(1 + i)(z - i) = (1 + i)[a + (b - 1)i] = a - b + 1 + (a + b - 1)i
Từ giả thiết ta có: (1 + i)(z - 1) + 2z = 2i
⇔ a - b + 1 + (a + b - 1)i + 2(a + bi) = 2i ⇔ (3a - b + 1) + (a + 3b - 1)i = 2i
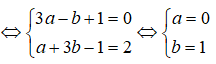
Suy ra z = 1 và
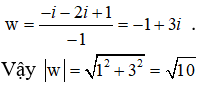
Câu 10: Cho số phức z thỏa mãn
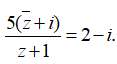
Khi đó môđun của số phức w = 1 + z + z2 là
A. 5 B. √13 C. 13 D. √5
Đặt z = a + bi(a, b ∈ R). Ta có
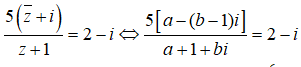
⇔ 5a - 5(b - 1)i = (2 - i)(a + 1 + bi)
⇔ 3a - b - 2 + (a - 7b + 6)i = 0
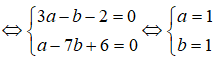
Suy ra z = 1 + i và w = 1 + (1 + i) + (1 + i)2 = 2 + 3i.
Vậy: |w| = √(4 + 9) = √13
Câu 11: Phương trình z2 - 2z + 3 = 0 có các nghiệm là
A. 2±2√2i B. -2±2√2i C. -1±2√2i D. 1±2√2i
Ta có: Δ' = 12 - 3 = -2 = 2i2. Phương trình có hai nghiệm: z1,2 = 1 ± 2i
Câu 12: Phương trình z4 - 2z2 - 3 = 0 có 4 nghiệm phức z1, z2, z3, z4. Giá trị biểu thức T = |z1|2 + |z2|2 + |z3|2 + |z4|2 bằng
A. 4 B. 8 C. 2√3 D. 2 + 2√3
Phương trình tương đương với: z2 = -1 = i2 hoặc z2 = 3. Các nghiệm của phương trình là: z1 = i, z2 = -i, z3 = √3, z4 = -√-3.
Vậy T = 1 + 1 + 3 + 3 = 8
Câu 13: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z - 2i| = 4 là
A. Đường tròn tâm I(1; -2) bán kính R = 4
B. Đường tròn tâm I(1; 2) bán kính R = 4
C. Đường tròn tâm I(0; 2) bán kính R = 4
D. Đường tròn tâm I(0; -2) bán kính R = 4
Đặt z = a + bi(a, b ∈ R). Ta có:
|z - 2i| = 4 ⇔ |a + (b - 2)i| = 4
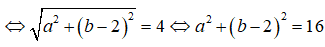
Vậy tập các điểm biểu diễn số phức z là đường tròn tâm I(0 ;2), bán kính R = 4
Câu 14: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z− + 3 - 2i| = 4 là
A. Đường tròn tâm I(3; 2) bán kính R = 4
B. Đường tròn tâm I(3; -2) bán kính R = 4
C. Đường tròn tâm I(-3; 2) bán kính R = 4
D. Đường tròn tâm I(-3; -2) bán kính R = 4
Đặt z = a + bi(a, b ∈ R). Ta có: |z− + 3 - 2i| = 4 ⇔ |a - bi + 3 - 2i| = 4
⇔ |(a + 3) - (b + 2)i| = 4
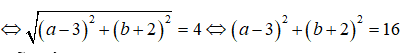
Vậy tập các điểm biểu diễn số phức z là đường tròn tâm I(-3 ;-2), bán kính R = 4


