Trắc nghiệm Phương trình bậc hai với hệ số thực có đáp án năm 2023
Trắc nghiệm Phương trình bậc hai với hệ số thực có đáp án năm 2023
Với bộ Trắc nghiệm Phương trình bậc hai với hệ số thực có đáp án năm 2023 sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Giải tích lớp 12.
Câu 1: Phương trình z2 -az + b = 0 (a, b ∈ R) có nghiệm z = 1 + i khi
A. a = 2, b = -2 B. a = 2, b = 2 C. a = -2, b = 2 D. a = -2, b = -2
Thay z = 1 + i vào phương trình đã cho ta có:
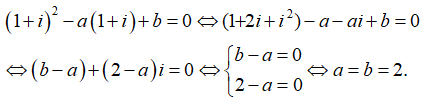
Chọn đáp án B.
Câu 2: Phương trình 2z2 + 4z + 5 = 0 có các nghiệm là
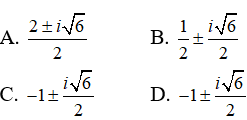
Ta có: Δ' = 4 - 10 = -6 = 6i2
Phương trình đã cho có các nghiệm là
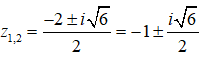
Chọn đáp án C.
Câu 3: Phương trình z2 - z + 1 = 0 có hai nghiệm là
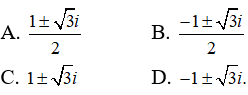
Ta có: Δ = 12 - 4 = -3 = 3i2
Các nghiệm của phương trình đã cho là
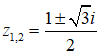
Chọn đáp án A.
Câu 4: Để phương trình z2 + bz + c = 0 nhận z1 = -4 + 2i và z2 = -4 - 2i làm nghiệm thì
A. b = -8, c = 20 B. b = -8, c = -20
C. b = 8, c = 20 D. b = 8, c = 20
Gọi z1, z2 là hai nghiệm của phương trình đã cho, áp dụng hệ thức Vi-ét ta có:
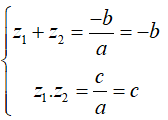
Để phương trình đã cho nhận z1, z2 làm nghiệm thì
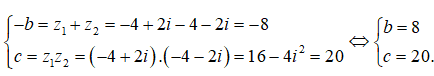
Chọn đáp án D.
Câu 5: Phương trình z2 + 6z + 15 = 0 có các nghiệm là z1, z2.Giá trị biểu thức T = |z1| + |z2| bằng:
A. 2√15 B. 6 C. 4√5 D. 2√3
Ta có:Δ' = 9 - 15 = -6 = 6i2
Các nghiệm của phương trình là z1 = - 3 - i√6, z2 = - 3 + i√6
Do đó
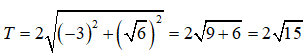
Chọn đáp án A.
Câu 6: Phương trình z1 = 1 + 2i, z2 = 2 - 3i có nghiệm là z = 2 + i khi
A. a = 1, b = 4 B. a = -1, b = 4 C. a = -1, b = -4 D. a = 1, b = -4
Thay z = 2 + i vào phương trình đã cho ta có:
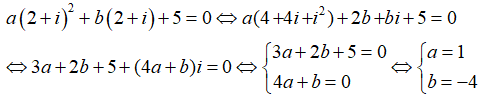
Câu 7: Phương trình (1 + i)2 = -7 + i có các nghiệm là
A. -1 - 2i và 1 + 2i B. -1 + 2i và 1 + 2i
C. -1 + 2i và 1 - 2i D. 1 + 2i và 1 - 2i
Phương trình đã cho tương đương với
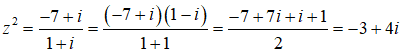
Viết -3 + 4i = 4i2 + 4i + 1 = (2i + 1)2, ta có: z2 = (2i + 1)2 <=> z = ±(2i + 1)
Chú ý: Nếu việc viết -3 + 4i = (2i + 1)2 gặp khó khăn thì có thể đặt z = a + bi (a, b ∈ R). Ta có :
(a + bi)2 = -3 + 4i <=> a2 - b2 + 2abi = -3 + 4i
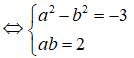
Từ phương trình thứ hai của hệ ta có b = 2/a
Thay vào phương trình thứ nhất của hệ ta có
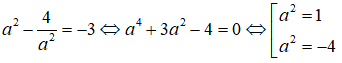
Vì a ∈ R và a2 ≥ 0 nên a2 = 1 hay a = ±1 . Từ đó ta có hai nghiệm : z1 = -1 - 2i và z2 = 1 + 2i
Câu 8: Phương trình z2 + 4x + 5 = 0 có các nghiệm là
A. 2 ± i B. -2 ± i C. 4 ± i D. -4 ± i
Ta có: Δ' = 22 - 1.5 = -1 = i2. Phương trình có hai nghiệm là:
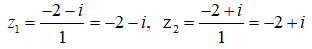
Câu 9: Phương trình z2 + 8z + 17 = 0 có hai nghiệm
A. 1 - i và 1 - 2i B. 4 - i và 4 + i
C. -4 - i và -4 + i D. -2 + 2i và -2 + 4i
Ta có: Δ = 16 - 17 = -1 = i2. Phương trình có các nghiệm là:
z1 = -4 - i, z2 = -4 + i
Câu 10: Phương trình z2 - 4z + 9 = 0 có hai nghiệm. Giá trị biểu thức T = |z1| + |z2| bằng
A. – 6 B. 6 C. 8 D. 2√3
Ta có: Δ' = 4 - 9 = -5 = 5i2. Phương trình có hai nghiệm là:
z1,2 = 2 ± i√5
Vậy T = 2√(4 + 5) = 2√9 = 6
Câu 11: Phương trình z4 + 3z2 - 4 = 0 có 4 nghiệm phức z1, z2, z3, z4. Giá trị biểu thức T = |z1| + |z2| + |z3| + |z4| bằng
A. 6 B. 2√2 C. 2 + 2√2 D. 4 + 2√2
Ta có
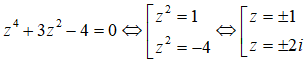
⇒ |z1| = |z2| = 1; |z3| = |z4| = 2
Vậy T = 1 + 1 + 2 + 2 = 6
Câu 12: Số phức z thỏa mãn
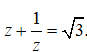
Giá trị biểu thức
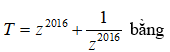
A. 1 B. 2 C. 3 D. 3672
Ta có: z + 1/z = √3 <=> z2 - √3z + 1 = 0 (1)
Xét phương trình (1): Ta có: Δ = (√3)2 - 4.1.1 = -1 = i2
Phương trình (1) có hai nghiệm là:
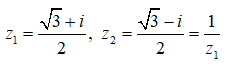
Do đó
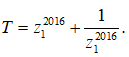
Ta có:
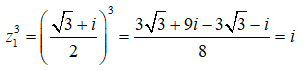
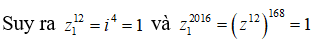
Vậy T = 1 + 1 = 2


