Trắc nghiệm Lôgarit có đáp án năm 2023
Trắc nghiệm Lôgarit có đáp án năm 2023
Với bộ Trắc nghiệm Lôgarit có đáp án năm 2023 sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Giải tích lớp 12.
Câu 1: Biết 3 + 2log2x = log2y . Hãy biểu thị y theo x
A. y = 2x+3 B. y = 8x2 C. y = x2+8 D. y = 3x2
3 + 2log2x = log2y ⇔ log223 + log2x2 = log2y
Chọn đáp án B
Câu 2: Nếu x = (log82)log28 thì log3x bằng:
A. -3 B. -1/3 C. 1/3 D. 3
x = (log82)log28 = (log232)log223 = (1/3)3 = 3-3 => log3x = -3
Chọn đáp án A
Câu 3: Độ pH của một chất được xác định bởi công thức pH = -log[H+] trong đó [H+] là nồng độ ion hyđrô trong chất đó tính theo mol/lít (mol/L). Xác định nồng độ ion H+ của một chất biết rằng độ pH của nó là 2,44
A. 1,1.108 mol/L C. 3,6.10-3 mol/L
B. 3,2.10-4 mol/L D. 3,7.10-3 mol/L
pH = -log[H+]
=> [H+] = 10-pH = 10-2,44 ≈ 0,00363 ≈ 3,6.10-3 (mol/L).
Chọn đáp án C
Câu 4: Rút gọn biểu thức
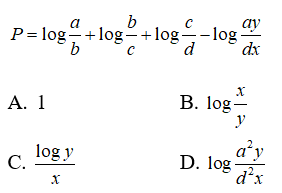
Ta có
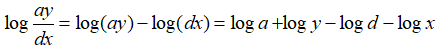
P = loga - logb + logb - logc + logc - logd - (loga + logy - logd - logx)
= -logy + logx = log(x/y)
Chọn đáp án B.
Câu 5: Tính giá trị biểu thức
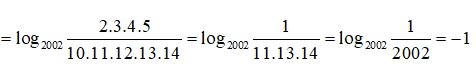
A. 0,01 B. 0,1 C. 1 D. 10
Biểu thức đã cho bằng
log100!2 + log100!3 + log100!4 + ... + log100!100 = log100!(2.3.4....10) = log100!100! = 1
Chọn đáp án C
Câu 6: Đặt a = log23, b = log35. Hãy tính biểu thức P = log660 theo a và b
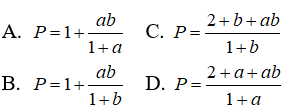
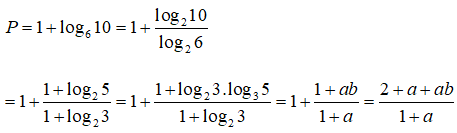
Chọn đáp án D
Câu 7:
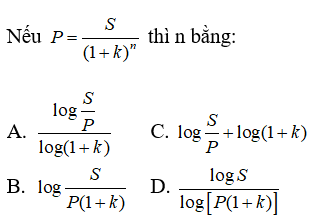
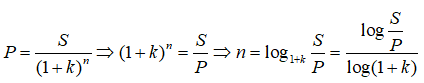
Chọn đáp án A.
Câu 8: Tính giá trị của biểu thức log3100 - log318 - log350
A. -3 B. -2 C. 2 D. 3
log3100 - log318 - log350
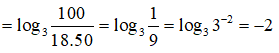
Câu 9: Tính giá trị của biểu thức (log23)(log94)
A. 2/3 B. 1 C. 3/2 D. 4
(log23)(log94) = (log23) = (log3222) = (log23)(log32) = 1
Câu 10: Tính giá trị của biểu thức
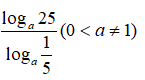
A. -2 B. 2 C. -3loga5 D. 3loga5
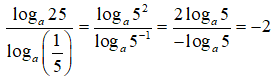
Câu 11: 10log7 bằng:
A. 1 B. log710 C. 7 D. log7
Sử dụng công thức alogab
⇒ 10log7 = 7
Câu 12: Cho P = log3(a2b3) (a,b là các số dương). Khẳng định nào sau đây là đúng ?
A. P = 6lpg3a.log3b B. P = 2log3a + 3log3b
C. P = (1/2)log3a + (1/3)log3b D. P = (log3a)2.(log3b)3
P = log3a2 + log3b3 = 2log3a + 3log3b
Câu 13: Đặt a = log27, b = log23. Tính log2(56/9) theo a và b
A. P = 3 + a - 2b B. P = 3 + a - b2 C. P = 3a/2b D. 3a/b2
P = log256 - log29 = log2(8.7) - log232 = log223 + log27 - 2log23 = 3 + log27 - 2log23 = 3 + a - 2b
Câu 14: Biết y = 23x. Hãy biểu thị x theo y
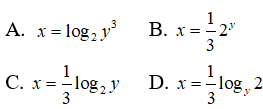
y = 23x ⇔ 3x = log2y ⇔ x = (1/3)log2y
Câu 15: Biết rằng log3y = (1/2)log3u + log3v + 1. Hãy biểu thị y theo u và v
A. y = 3√uv B. y = 3u2v C. y = 3 + √u + v D. y = (√uv)3
log3y = (1/2)log3u + log3v + 1 <=> log3y = log3u1/2 + log3v + log33 = log3(√u.v.3) => y = 3√u.v
Câu 16: Tìm số k sao cho 2x = ekx với mọi số thực x
A. k = √2 B. k = 2x C. k = log2e D. k = ln2
Ta có: 2x = (eln2)x = exln2 = ekx => k = ln2
Câu 17: Độ pH của một chất được xác định bởi công thức pH = -log[H+] trong đó H+ là nồng độ ion hyđrô trong chất đó tính theo mol/lít (mol/L). Xác định nồng độ ion H+ của một chất biết rằng độ pH của nó là 8,06
A. 8,7.10-9 mol/L B. 2,44.10-7 mol/L
C. 2,74,4 mol/L D. 3,6.10-7 mol/L
pH = -log[H+] ⇒ [H+] = 10-pH = 10-8,06 ≈ 8,7.10-9(mol/L)
Câu 18: log125 bằng
A. 5log3 B. 3 - 3log2 C. 100log1,25 D. (log25)(log5)
log125 = log(1000/8) = log1000 - log8 = log103 - log23 = 3 - 3log2
Câu 19: Cho a, b, c là các số dương. Tính giá trị của biểu thức logab2.logbc2.logca2
A. 1/8 B. 1 C. 8 D. 6
logab2.logbc2.logca2 = (2logab)(2logbc)(2logca) = 8logab.logbc.logca = 8logac.logca = 8
Câu 20: Tính giá trị của biểu thức
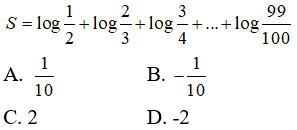
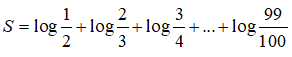
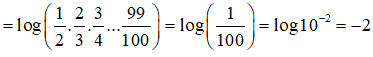
Câu 21: Với 0 < x ≠ 1 , biểu thức
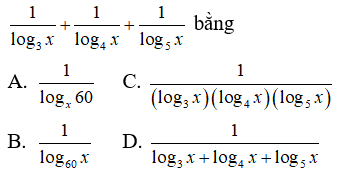
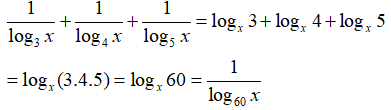
Câu 22: Nếu a = log8225 và b = log215 thì giữa a và b có hệ thức

a = log8225 = log23152 = (2/3)log215 = 2b/3
Câu 23: Khối lượng m của một chất phóng xạ thay đổi theo thời gian t tuân theo công thức
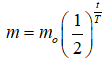
trong đó m0 là khối lượng chất phóng xạ ban đầu, T là chu kì bán rã. Nếu viết phương trình này dưới dạng m = m0e-kt thì :
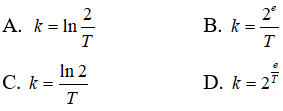
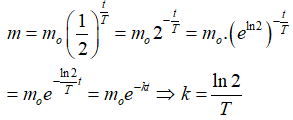
Câu 24: Đặt log83 = p và lognx = 3logmx . Hãy biểu thị log5 theo p và q
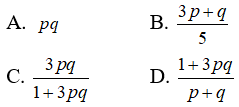
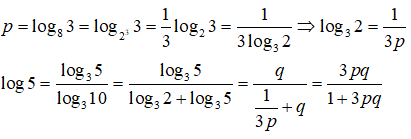
Câu 25: Cho m, n > 1 và lognx = 3logmx với mọi x > 0. Hãy biểu thị m theo n
A. m = n3 B. m = 1/n3 C. m = ∛n D. m = 1/∛n
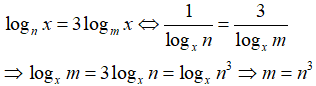
Câu 26: Biết rằng 4a = 5, 5b = 6, 6c = 7, 7d = 8. Tính abcd
A. 1/2 B. 3/2 C. 2 D. 2/3
Từ giả thiết ta có: a = log45, b = log56, c = log67, d = log78
=> abcd = log45.log56.log67.log78 = log46log67log78 = log47.log78 = log48 = log2223 = (3/2)log22 = 3/2
Câu 27: Cho b > 1, sinx > 0, cosx > 0 và logbsinx = a. Khi đó logbcosx bằng