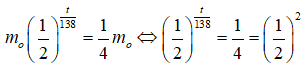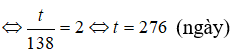Đề kiểm tra 1 tiết Giải tích 12 chương 2 có đáp án năm 2023

---

Đề kiểm tra 1 tiết Giải tích 12 chương 2 có đáp án năm 2023

Với bộ Đề kiểm tra 1 tiết Giải tích 12 chương 2 có đáp án năm 2023 sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Giải tích lớp 12.

Câu 1: Rút gọn biểu thức

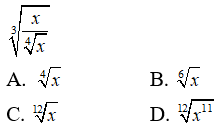
Câu 2: Khẳng định nào sau đây sai?

A. log1 = ln1    C. 10(log5) = log50

B. log100 + 3 = log10⁵   D. log100 + log0,01 = 0

Câu 3: Tính giá trị biểu thức

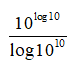
A. -1    B. 1   C. 10   D. 1/10

Câu 4: Giải phương trình 1000000^x = 10

A. x = log6   B. x = 1/5    C. x = 1/6   D. x = -6

Câu 5: Cho phương trình log₅(x + 4) = 3 . Nghiệm của phương trình này nằm trong khoảng nào sau đây?

A. (100; 125)   B. (10; 20)   C. (200; 250)   D. (125; 150)

Câu 6: Giải bất phương trình

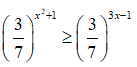
A. -2 ≤ x ≤ -1    C. x ≤ -2 hoặc x ≥ -1

B. 1 ≤ x ≤ 2    D. x ≤ 1 hoặc x ≥ 2

Câu 7: Giải bất phương trình log₃36 - log₃x > 1

A. 0 < x < 12    B. x < 12   C. x > 12    D. x < 1/12

Câu 8: Cho

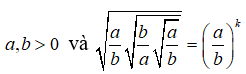
Tìm giá trị của k

Câu 9: Cho hàm số

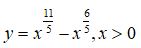
Khẳng định nào sau đây là đúng?

A. Hàm số có hai điểm cực trị

B. Hàm số không có điểm cực trị nào

C. Hàm số có đúng một điểm cực trị và nó là điểm cực tiểu

D. Hàm số có đúng một điểm cực trị và nó là điểm cực đại

Câu 10: Tìm giá trị lớn nhất của hàm số y = ∛x(8 - x) trên đoạn [0; 8]

A. 4∛4   B. 5∛5    C. 6∛2    D. 10∛2

Câu 11: Nếu y = (log₂3)(log₃4)(log₄5)...(log₃₁32) thì

A. y = 5    B. 4 < y < 5    C. 5 < y < 6   D. y = 6

Câu 12: Đặt log80 = a, log45 = b . Hãy tính log36 theo a và b

A. a + b - 1   B. b - a + 1    C. a + b - 2   D. b - a + 2

Câu 13: Ông A gửi tiết kiệm một số tiền vào ngân hàng với hình thức lãi kép và lãi suất 6,8% một năm. Ông A muốn sau 5 năm có thể rút hết số tiền tiết kiệm trên (cả gốc lẫn lãi) để nhận được ít nhất 100 triệu đồng. Hỏi lúc đầu ông A phải gửi số tiền tối thiểu là bao nhiêu? Biết rằng số tiền ông A gửi là số tròn triệu đồng.

A. 70 triệu đồng   B. 71 triệu đồng   C. 72 triệu đồng   D. 73 triệu đồng

Câu 14: Tìm đạo hàm của hàm số

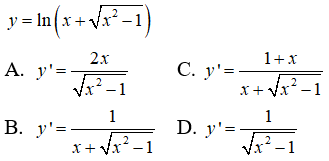
Câu 15: Tìm các giá trị x thỏa mãn

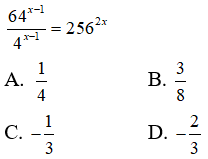
Câu 16: Tính tích các nghiệm của phương trình 2^2x - 8.2^x + 12 = 0

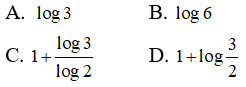
Câu 17: Giả sử x là nghiệm của phương trình

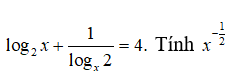
A. 1/2   B. 1   C. 2   D. 4

Câu 18: Giải bất phương trình 9^x ≤ 2.3^x + 3

A. 1/3 ≤ x ≤ 1   B. 1/3 ≤ x ≤ 3   C. x ≤ 1    D. -1 ≤ x ≤3

Câu 19: Giải bất phương trình

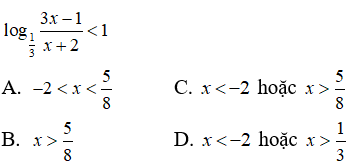
Câu 20: Tìm các khoảng đồng biến của hàm số

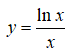
A. (0; e)   B. (-∞; e)    C. (0; 1)   D. (1; +∞)

Câu 21: Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số

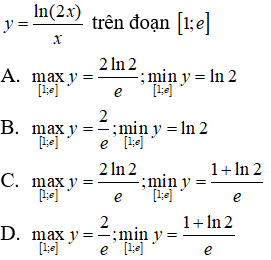
Câu 22: Biết rằng 2.4^x + 6^x = 9^x và x = log_2/3a . Tìm giá trị của a

A. 1/2    B. 2/3     C. 2   D. 3/2

Câu 23: Tính (log₂x)² , biết rằng log₂(log₈x) = log₈(log₂x)

A. 27     B. 1/27    C. 3√3    D. 1/3√3

Câu 24: Cho hai số x, y thỏa mãn đồng thời

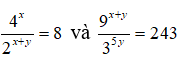
Tính xy

A. -4   B. 4   C. 12    D. 12/5

Câu 25: Khối lượng của một chất phóng xạ giảm theo thời gian t (tính bằng ngày) theo công thức

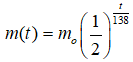
trong đó m₀ là khối lượng của chất đó tại thời điểm được chọn làm mốc thời gian. Hỏi sau thời gian bao lâu thì khối lượng của chất phóng xạ đó bằng 1/4 khối lượng ban đầu?

A. 69 ngày    B. 138 ngày   C. 276 ngày   D. 414 ngày

Hướng dẫn giải và Đáp án

Câu	1	2	3	4	5	6	7	8	9	10
Đáp án	A	B	B	C	A	B	A	D	C	C
Câu	11	12	13	14	15	16	17	18	19	20
Đáp án	A	C	C	D	C	C	A	C	C	A
Câu	21	22	23	24	25
Đáp án	D	A	A	B	C

Câu 1:

Ta có:

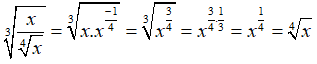
Chọn A

Câu 2:

* log1 = ln1 = 0

* log100 + 3 = 2 + 3 = 5 = log10⁵

* 10(log5) = log5¹⁰ ≠ log50

* log100 + log0.01 = log10² + log10^-2 = 2 + (-2) = 0

Do đó, khẳng định B sai

Câu 3:

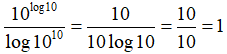
Câu 4:

1000000^x = 10 ⇔ 10^6x = 10 ⇔ 6x = 1 ⇔ x = 1/6

Câu 5:

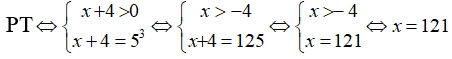
Ta có: 121 ∈ (100; 125)

Câu 6:

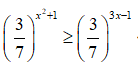
⇔ x² + 1 ≤ 3x - 1 (vì (3/7) < 1) ⇔ x² - 3x + 2 ≤ 0 ⇔ 1 ≤ x ≤ 2

Câu 7:

Điều kiện: x > 0

log₃36 - log₃x > log₃36 - 1 > log₃x ⇔ log₃x < log₃36 - log₃3

⇔ log₃x < log₃(36/3) ⇔ log₃x < log₃12 ⇔ 0 < x < 12

Câu 8:

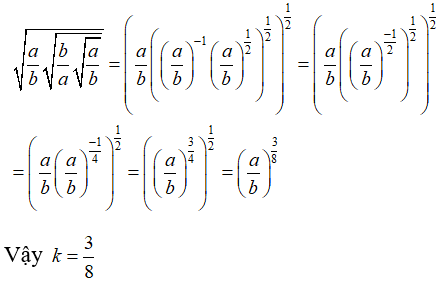
Câu 9:

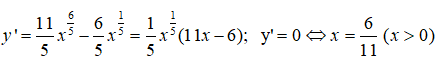
Ta thấy y’ đổi dấu từ âm sang dương khi đi qua x = 6/11 nên hàm số có đúng một điểm cực trị x = 6/11 và đó là điểm cực tiểu

Câu 10:

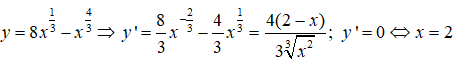
Ta có: y(0) = y(8) = 0, y(2) = 6∛2

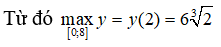
Câu 11:

Sử dụng công thức log_ablog_bc = log_ca ta tính được

y = [(log₂3)(log₃4)](log₄5)...(log₃₁32) = [log₂4](log₄5)...(log₃₁32)

= [(log₂4)(log₄5)](log₅6)...(log₃₁32) = [log₂3](log₅6)...(log₃₁32)

= ... = log₂32 = log₂2⁵ = 5

Cách khác:

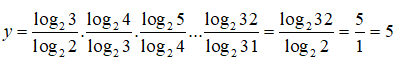
Câu 12:

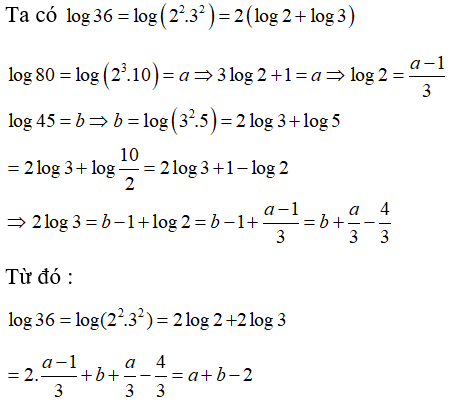
Câu 13:

Gọi P là số tiền ông A gửi lúc đầu. Để rút được 100 triệu đồng sau 5 năm ta phải có

P(1 + 0,068)⁵ = 100000000

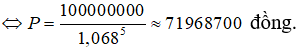
Vì số tiền gửi là tròn triệu đồng nên ông A phải gửi tối thiểu 72 triệu đồng.

Câu 14:

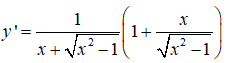
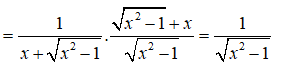
Câu 15:

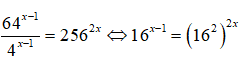
⇔ 16^{x - 1} = 16^4x ⇔ x - 1 = 4x ⇔ x = -1/3

Câu 16:

Đặt t = 2^x (t > 0) nhận được phương trình t² - 8t + 12 = 0

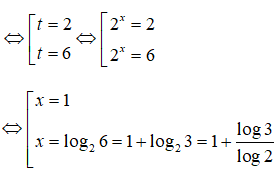
Tích hai nghiệm bằng 1 + log3.log2

Câu 17:

Điều kiện: x > 0

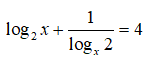
⇔ log₂x + log₂x = 4 ⇔ log₂x = 2 ⇔ x = 2² = 4

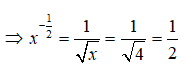
Câu 18:

Bất phương trình đã cho tương đương với 3^2x - 2.3^x - 3 ≤ 0

Đặt t = 3^x > 0, nhận được bất phương trình:

t² - 2t - 3 ≤ 0 ⇔ -1 ≤ t ≤ 3

⇒ 0 < t ≤ 3 ⇔ 3^x ≤ 3 ⇔ x ≤ 1

Câu 19:

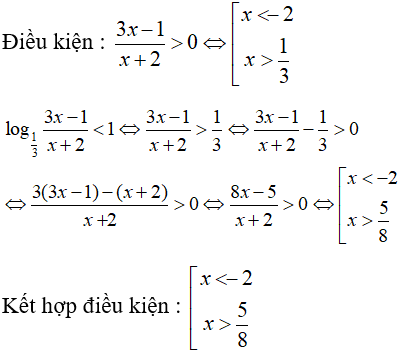
Câu 20:

Tập xác định: D = (0; +∞)

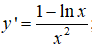
y' ≥ 0 ⇔ lnx ≤ 1 ⇔ 0 ≤ x ≤ e

Từ bảng xét dấu của y’ ta thấy hàm số đồng biến trên (0; e)

Câu 21:

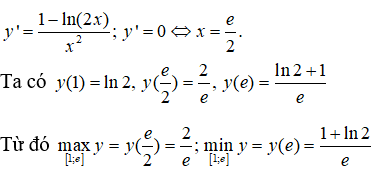
Câu 22:

2.4^x + 6^x = 9^x ⇔ 2.2^2x + 2^x.3^x - 3^2x = 0

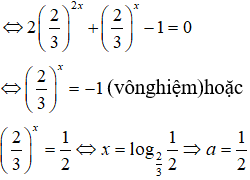
Câu 23:

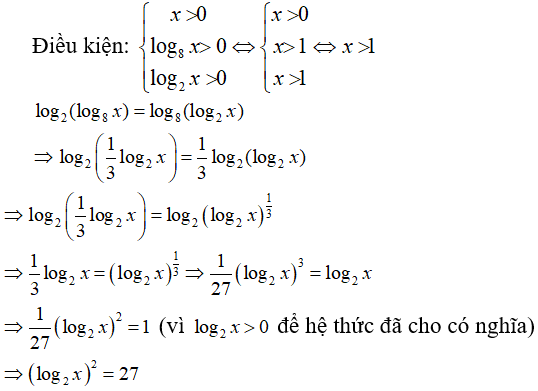
Câu 24:

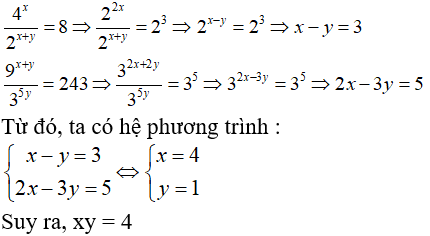
Câu 25:

Để khối lượng của chất phóng xạ đó bằng 1/4 khối lượng ban đầu thì

m(t) = 1/4 m₀

Ta có: