Trắc nghiệm Số phức có đáp án năm 2023 (phần 2)
Trắc nghiệm Số phức có đáp án năm 2023 (phần 2)
Với bộ Trắc nghiệm Số phức có đáp án năm 2023 (phần 2) sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Giải tích lớp 12.
Câu 1: Môđun của số phức z = -3 + 4i là
A. 5 B. -3 C. 4 D. 7
Ta có: z = -3 + 4i
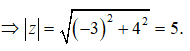
Câu 2: Môđun của số phức z = 2 - √3i là
A. √7 B. 2 + √3 C. 2 - √3 D. 7
Ta có: z = 2 - √3i
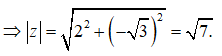
Câu 3: Số phức z = 1 - 2i có điểm biểu diễn là
A. M (1; 2) B. M (1; -2) C. M (-1; 2) D. M (-1; -2)
Số phức z = 1 - 2i có điểm biểu diễn là M(1; -2).
Câu 4: Hai điểm biểu diễn hai số phức liên hợp z = 1 + i và z− = 1 - i đối xứng nhau qua
A. Trục tung B. Trục hoành C. Gốc tọa độ D. Điểm I (1; -1)
Hai điểm biểu diễn của z = 1 + i và z− = 1 - i là M(1; 1) và N(1; -1) đối xứng với nhau qua trục Ox.
Câu 5: Tập hợp các điểm biểu diễn số phức z thỏa mãn |z| = 2 là
A. Hai đường thẳng B. Đường tròn bán kính bằng 2
C. Đường tròn bán kính bằng 4 D. Hình tròn bán kính bằng 2.
Gọi M là diểm biểu diễn của z. Ta có: |z| = 2 ⇔ OM = 2
Vậy quỹ tích của M là đường tròn tâm là gốc tọa độ O và bán kính R = 2.
Câu 6: Gọi A, B là các điểm biểu diễn của các số phức z1 = -1 + 2i, z2 = 2 + 3i . Khi đó, độ dài đoạn thẳng AB là
A. √26 B. √5 + √13 C. √10 D. 10
Ta có: A(-1;2), B(2,3). Do đó:
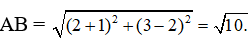
Câu 7: Cho số phức z = 2 – 2i. Tìm khẳng định sai.
A. Phần thực của z là: 2.
B. Phần ảo của z là: -2.
C. Số phức liên hợp của z là z− = -2 + 2i.
D. Môđun của z là
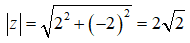
Số phức liên hợp của z là z− = 2 + 2i nên khẳng định C là sai.
Chọn đáp án C.
Câu 8: Cho số phức z = -1 + 3i. Phần thực, phần ảo của z− là
A. -1 và 3 B. -1 và -3 C. 1 và -3 D. -1 và -3i.
Ta có z = -1 + 3i => z− = -1 - 3i
Vậy phần thực và phần ảo của z− là -1 và -3.
Chọn đáp án B.
Câu 9: Môđun của số phức z thỏa mãn z− = 8 - 6i là
A. 2 B. 10 C. 14 D. 2√7
Ta có
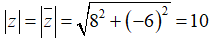
Chọn đáp án B.
Câu 10: Tìm các số thực x, y sao cho (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
A. x = 3, y = 1 B. x = 3, y = -1
C. x = -3, y = -1 D. x = -3, y = 1
Ta có (x – 2y) + (x + y + 4).i = (2x + y) + 2yi.
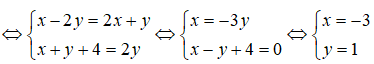
Vậy x = -3, y = 1.
Chọn đáp án D.
Câu 11: Hai số phức z1 = x - 2i, z22 + yi (x, y ∈ R) là liên hợp của nhau khi
A. x = 2, y = -2 B. x = -2, y = -2 C. x = 2, y = 2 D. x = -2, y = 2
Ta có z1− = x + 2i. Do đó, hai số phức đã cho gọi là liên hợp của nhau khi và chỉ khi
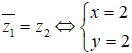
Vậy x= 2, y = 2. Chọn đáp án C.
Câu 12: Tập hợp các điểm biểu diễn số phức z thòa mãn |z| = |1 + i| là
A. Hai điểm B. Hai đường thẳng
C. Đường tròn bán kính R=2 D. Đường tròn bán kính R= √2 .
Ta có |1 + i| = √(1 + 1) = √2. Gọi M là điểm biểu diễn của z ta có |z| = OM.
Do đó: |z| = |1 + i| ⇔ OM = √2
Vậy tập hợp các điểm M biểu diễn số phức z là đường tròn tâm O, bán kính R= √2 .
Chọn đáp án D.
Câu 13: Phần thực của số phức z = -i là
A. -1 B. 1 C. 0 D. -i
Ta có: z = -i = 0 - i nên phần thực của số phức z = -i là 0
Câu 14: Phần ảo của số phức z = -1 là
A. -i B. 1 C. -1 D. 0
Ta có: z= -1 = -1 + 0.i nên phần ảo của số phức z = -1 là 0
Câu 15: Số phức liên hợp của số phức z = 1 + i là
A. 1 – i B. -1 – i C. -1+ i D. 1 + i
Số phức liên hợp của số phức z = 1 + i là z− = 1 - i
Câu 16: Cho z = 2i -1. Phần thực và phần ảo của z− là
A. 2 và 1 B. -1 và -2 C. 1 và 2i D. -1 và -2i
Ta có z = 2i - 1 = -1 + 2i ⇔ z− = -1 - 2i. Vậy phần thực của z− là -1 và phần ảo của z− là -2.


