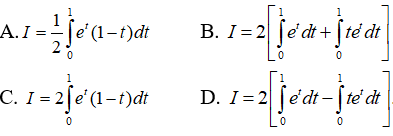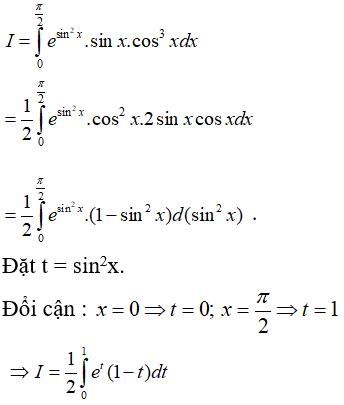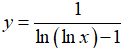Trắc nghiệm Ôn tập Giải tích 12 có đáp án năm 2023 (phần 2)
Trắc nghiệm Ôn tập Giải tích 12 có đáp án năm 2023 (phần 2)
Với bộ Trắc nghiệm Ôn tập Giải tích 12 có đáp án năm 2023 (phần 2) sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Giải tích lớp 12.
Câu 1: Tính giá trị biểu thức log35.log49.log52
A. 1/2 B. 1 C. 2 D. 3
log35. log49. log52 = (log35.log52).log2232 = log32.log23 = 1
Câu 2: Tìm đạo hàm của hàm số y = (√3)x2
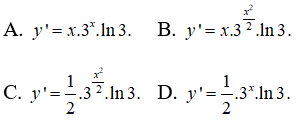
y' = (√3)x2.ln√3(x2)'
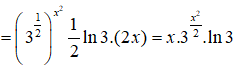
Câu 3: Nếu 4x - 4x - 1 = 24 thì (2x)x bằng
A. 5√5 B. 25 C. 25√5 D. 125.
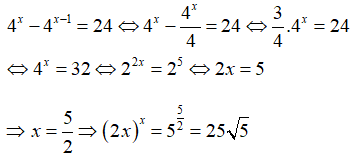
Câu 4: Giải phương trình log3x + log9x + log81x = 7
A. x = 27 B. x = 81 C. x = 729 D. x = 243
Điều kiện : x > 0
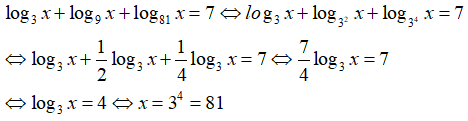
Kết hợp điều kiện, vậy x = 81.
Câu 5: Nếu (log3x)(log2xy) = logxx2 thì y bằng
A. 9 B. 9/2 C. 18 D. 81
Điều kiện : x > 0 ; y > 0.
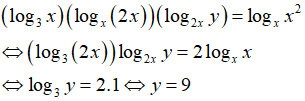
Câu 6: Tìm miền xác định của hàm số
A. D = (1; +∞)\{ee} B. D = (0; +∞)\{e}
C. D = (ee; +∞) D. D = (1; +∞)\{e}
Điều kiện
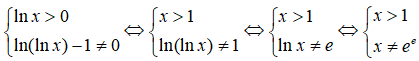
Vậy miền xác định của hàm số là D = (1; +∞)\{ee}
Câu 7: Ngày 15 tháng 2 năm 2010 ông A gửi vào ngân hàng 500 triệu đồng với hình thức lãi kép và lãi suất 10,3% một năm. Tại thời điểm đó ông A dự tính sẽ rút hết tiền ra vào 15 tháng 2 năm 2013. Nếu trong khoảng thời gian đó lãi suất không thay đổi thì số tiền mà ông A rút được là bao nhiêu? Làm tròn kết quả đến hàng nghìn.
A. 608305000 đồng. B. 665500000 đồng.
C. 670960000 đồng. D. 740069000 đồng.
Sau 3 năm từ 2010 đến 2013, số tiền ông A rút được : 500000000.(1 + 0,103)3 = 670959863 ≈ 970960000 (đồng)
Câu 8: Tìm giá trị lớn nhất của hàm số y = x2e-x trên đoạn [-1; 4]
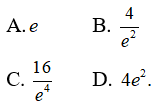
y' = 2xe-x - x2e-x = xe-x(2 - x); y' = 0 <=> x = 0 hoặc x = 2
y(-1) = e, y(0) = 0, y(2) = 4/e2, y(4) = 16/e4
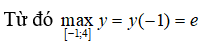
Câu 9: Tìm tập nghiệm của phương trình log(x + 3) + log(x - 1) = log(x2 - 2x -3)
A. ∅ B. {0} C. R D. (1; +∞)
Điều kiện x > 3. Khi đó: log(x + 3) + log(x - 1) = log(x2 - 2x - 3)
<=> log[(x + 3)(x - 1)] = log(x2 - 2x - 3) <=> x2 + 2x - 3 = x2 - 2x + 3
<=> 4x = 0 <=> x = 0 (loại).
Vậy phương trình vô nghiệm
Câu 10: Tìm m để y = x3 - 3x2 +mx - 1 có hai điểm cực trị tại x1, x2 thỏa mãn
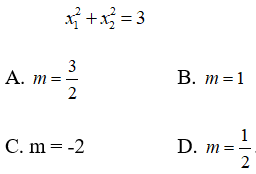
y' = 3x2 - 6x + m.
Hàm số có cực trị khi y' = 0 có hai nghiệm phân biệt :
Câu 11: Tìm m để hàm số y = (1/3)x3 - x2 - mx + 1 luôn đồng biến trên từng khoảng xác định của nó
A. m < - 1 B. m > -1 C. m ≤ -1 D. m > -1
Tập xác định : D = R
Ta có : y'=x2 - 2x - m
Để hàm số đã cho đồng biến trên từng khoảng xác định khi và chỉ khi:
y' = x2 - 2x - m ≥ 0, ∀ x ⇔ Δ' = 1 + m ≤ 0 ⇔ m ≤ -1
Câu 12: Tìm m để phương trình |x3 + 3x2 - 9x + 2| = m có 6 nghiệm phân biệt
A. 0 < m < 3 B. m = 3 C. 3 < m < 29 D. m > -3
Vẽ đồ thị hàm số y = x3 + 3x2 – 9x + 2 (C)
Giữ phần đồ thị (C) phía trên trục Ox, lấy đối xứng phần đồ thị (C) dưới trục Ox qua trục Ox.
Bỏ phần đồ thị dưới trục Ox ta được đồ thị y = |x3 + 3x2 – 9x + 2|.
Dựa vào đồ thị ta có đáp án A.
Câu 13: Tìm m để hàm số y = -x3 + (2m + 1)x2 - (m2 - 3m +2)x - 4 có cực đại, cực tiểu nằm về hai phía so với trục tung
A. m ∈ (1; 2) B. m ∈ [1; 2]
C. m ∈ (- ∞; 1) ∪ (2; +∞) D. m ∈ (- ∞; 1] ∪ [2; +∞)
y' = -3x2 + 2(2m + 1)x - m2 + 3m - 2
Để hàm số đã cho có cực đại, cực tiểu nằm về hai phía so với trục tung khi và chỉ khi phương trình y’ = 0 có hai nghiệm x1, x2 trái dấu.
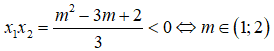
Câu 14: Tìm m để hàm số y = x3 - 3mx2 + 12x - 2 nghịch biến trên khoảng (1; 4)
A. m ≥ 5/2 B. m ≤ 5/2 C. m ≤ 2 D. Đáp án khác
Tìm m để hàm số y = x3 - 3mx2 + 12x - 2 nghịch biến trên khoảng ( 1; 4)
y' = 3x2 - 6mx + 12 = 3(x2 - 2mx + 4)
y' = 0 ⇔ x2 - 2mx + 4 = 0
Đặt f(x) = x2 – 2mx + 4
* Trường hợp 1:
y' ≤ 0 ∀ x ∈ R ⇔ Δ' = m2 - 4 ≤ 0 ⇔ - 2 ≤ m ≤ 2
Khi đó hàm số đã cho nghịch biến trên R.
* Trường hợp 2. Giả sử phương trình y’ = 0 có 2 nghiệm phân biệt x1; x2 . Để hàm số nghịch biến trên khoảng ( 1; 4) khi
x1 ≤ 1 < 4 ≤ x2
Câu 15: Đồ thị hàm số
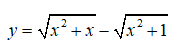
có đường tiệm cận ngang có phương trình là
A. y = 1 B. y = 0 C. y = 1/2 D. y = ±1/2
Ta có:
Câu 16: Hệ số góc của tiếp tuyến của đồ thị hàm số
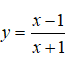
tại giao điểm của đồ thị hàm số với trục tung bằng
A. –2 B. 2 C. 1 D. –1.
Giao điểm với trục tung B(0 ;-1). Ta có
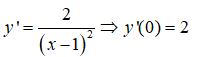
Hệ số góc của tiếp tuyến của đồ thị hàm số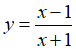 
tại giao điểm của đồ thị hàm số với trục tung bằng k = 2.
Câu 17: Cho đồ thị hàm số y = x3 - 2x2 + 2x . Gọi x1, x2 là hoành độ các điểm M, N trên (C) mà tại đó tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2016. Khi đó x1 + x2 bằng:
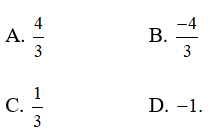
Ta có y' = 3x2 - 4x + 2
Do tiếp tuyến của (C) vuông góc với đường thẳng y = -x + 2016 nên hệ số góc của tiếp tuyến là k = 1
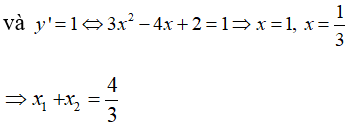
Câu 18: Cho hàm số y = x3 - 3x + 2 (C) . Tìm phương trình tiếp tuyến của (C), biết tiếp tuyến đi qua điểm A(-1; 0).
A. y = 0 B. y = x + 1 C. y = x - 1 D. y = 2
Ta có: y’ = 3x2 – 3
Phương trình tiếp tuyến tại điểm A (x0; x03 - 3x0 + 2) là:
y = (3x02 - 3)(x - x0) + x03 - 3x0 + 2 (*)
Để tiếp tuyến này đi qua điểm (-1; 0) thì:
0 = (3x02 - 3)(-1 - x0) + x03 - 3x0 + 2
⇔ 0 = -3x02 - 3x03 + 3 + 3x0 + x03 - 3x0 + 2
⇔ -2x03 - 3x02 + 5 = 0 ⇒ x0 = 1
Thay vào (*) ta được phương trình tiếp tuyến cần tìm là :y = 0
Câu 19: Tìm m để đồ thị hàm số y = x3 + 3x2 + mx + 2m cắt đường thẳng y = -x + 2 tại 3 điểm.
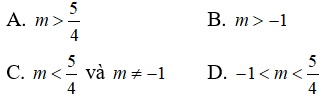
Chọn đáp án C
Câu 20: Tìm m để đồ thị hàm số
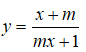
có đường tiệm cận ngang
A. m ≠ 0 B. m ≠ ±1 C. m ≠ 1 D. Cả A và B.
* Nếu m = 0 thì y = x nên hàm số đã cho không có tiệm cận ngang.
* Nếu m = 1 thì y = 1 nên hàm số không có tiệm cận ngang.
* Nếu m = -1 thì y = -1 nên hàm số không có tiệm cận ngang.
Vậy để hàm số đã cho có tiệm cận ngang thì m ≠ 0 và m ≠ ±1;
Câu 21: Hàm số y = (x - 1)ex với x ∈ [-1; 1] đạt giá trị lớn nhất tại x bằng
A. 1 B. -1 C. 0 D. 1/2
Vẽ đồ thị y' = xex. y' = 0 => x = 0
y(0) = -1; y(-1) = -2/e; y(1) = 0
Vậy hàm số đã cho đạt giá trị lớn nhất tại x = 1.
Câu 23: Hàm số
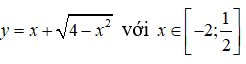
đạt giá trị lớn nhất tại x bằng
A. 1 B. 1/2 C. -2 D. -1.
Ta có:
Câu 24: Tìm m để đồ thị hàm số y = x4 - 2m2x2 + 1 có ba cực trị tạo thành tam giác vuông.
A. m = ± 1 B. m = ± 2 C. m = 3 D. Đáp án khác.
Chọn đáp án A
Câu 24: Cho
Khẳng định nào sai?
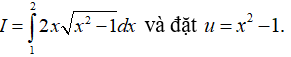
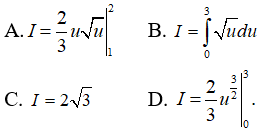
Dễ thấy B, C, D là các khẳng định đúng, còn khẳng định A sai vì đổi biến mà không đổi cận
Câu 25: Biến đổi
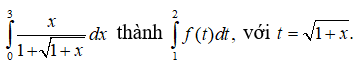
Khi đó, f(t) là hàm nào trong các hàm số sau?
A. f(t) = 2t2 - 2t B. f(t) = t2 + t C. f(t) = t2 - t D. f(t) = 2t2 + 2t
Ta có:
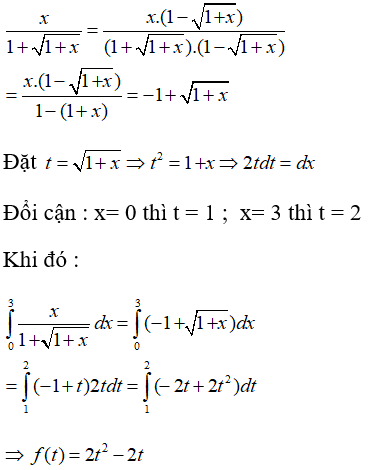
Câu 26: Diện tích hình giới hạn bởi đường cong y = x2 + 1 tiếp tuyến với đường cong này tại M(2; 5) và trục là:
A. 0 B. -8/3 C. 8/3 D. Kết quả khác.
Ta có : y’ = 2x nên y'(2) = 4
Phương trình tiếp tuyến với y = x2 + 1 tại M(2 ;5) là :
y = y'(2)(x - 2) + 5 => y = 4(x - 2) + 5 = 4x - 3
Xét phương trình hoành độ giao điểm của hai đồ thị :
x2 + 1 = 4x - 3 => x = 2 .
Ta có diện tích hình phẳng cần tính là:
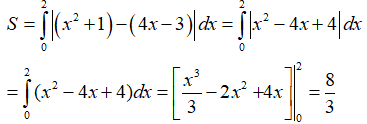
Câu 27: Thể tích vật tròn xoay khi quay hình phẳng giới hạn bởi các đường y = 4/x, y = 0, x = 1, x = 4 quanh trục Ox là:
A. 6π B. 4π C. 12π D. 8π
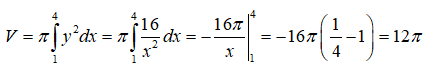
Câu 28: Thể tích vật tròn xoay khi quay hình phẳng giới hạn bởi các đường
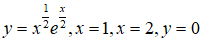
quanh trục Ox là:
A. π(e2 + e) B. π(e2 - e) C. πe2 D. πe
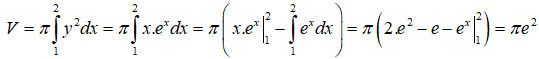
Câu 29: Phần thực và phần ảo của số phức z thỏa mãn z− = (1 + 2i)2 + (1 - 2i)3 là
A. 14 và 6i B. –14 và 6 C. 14 và – 6 D. –14 và –6.
Ta có:
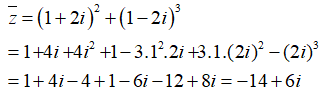
Suy ra z = -14 - 6i. Vậy phần thực và phần ảo của z là: -14 và - 6
Câu 30: Thực hiện phép tính T = 3i(5 + 2i) + (2 - 5i)(3 + 7i) ta có:
A. T = 35 + 14i B. T = 35 - 24i C. T = -35 + 14i D. T = -35 - 14i
Ta có: T = 3i(5 + 2i) + (2 - 5i)(3 + 7i)
T = 15i + 6i2 + 6 + 14i - 15i - 35i2 = 15i - 6 + 6 + 14i - 15i + 35 = 35 + 14i
Câu 31: Thực hiện phép tính
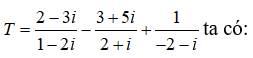
A. T = 1 + i B. T = 1 - i C. T = -1 + i D. T = -1 - i
Ta có
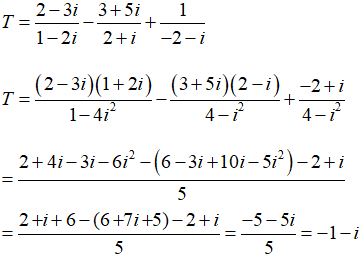
Câu 32: Các số thực x, y thỏa mãn: (x + 2y) + (2x - y)i = 6 + 7i. Giá trị biểu thức T = x + y bằng:
A. 4 B. 5 C. 6 D. 7.
Ta có: (x + 2y) + (2x - y)i = 6 + 7i
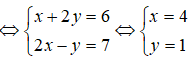
Vậy: T = 4 + 1 = 5
Câu 33: Phương trình z2 - 8z + 20 = 0 có hai nghiệm là
A. 8 ± 4i B. -8 ± 4i C. -4 ± 2i D. 4 ± 2i
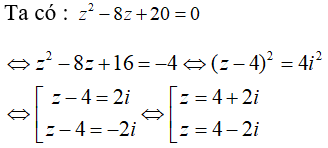
Câu 34: Số phức z = a + bi có phần thực, phần ảo là các số nguyên và thỏa mãn: z3 = 2 + 11i. Giá trị biểu thức T = a + b là
A. 2 B. 3 C. 4 D. 5
Ta có: z3 = a3 + 3a2bi + 3ab2i2 + b3i3 = a3 - 3ab2 + (3a2b - b3)i
Lại có:
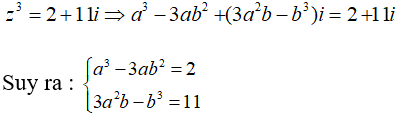
Từ phương trình thứ nhất ta có: a(a2 - 3b2). Vì a,b nguyên nên a là ước của 2.
Nếu a=1 thì 1 - 3b2 = 2. Suy ra b2 = -1/3 ∉ Z (loại)
Nếu a=-1 thì b = ±1 , không thỏa mãn phương trình thứ hai của hệ.
Nếu a=-2 thì b2 = 5/3 ∉ Z (loại).
Nếu a=2 thì b = ±1 . Kết hợp với phương trình thứ hai ta có: a = 2, b = 1
Vậy T = 3
Câu 35: Tập hợp các điểm biểu diễn số phức z thỏa mãn |i(z - 1) + 2| = |3 - 4i| là
A. Đường tròn tâm I(1; 2) bán kính R = 5
B. Đường tròn tâm I(1; -2) bán kính R = 5
C. Đường tròn tâm I(-1; 2) bán kính R = 5
D. Đường tròn tâm I(-1; -2) bán kính R = 5
Đặt z = a + bi (a, b ∈ R). Ta có:
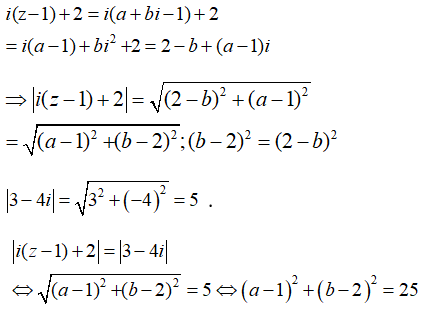
Do đó: |i(z - 1) + 2| = |3 - 4i| <=> (a - 1)2 + (b - 2)2 = 25
Tập hợp các điểm M(a,b) biểu diễn của số phức z là đường tròn tâm I(1;2), bán kính là R=5
Câu 36: Cho số phức z thỏa mãn |z− + 1 - i| = |z|. Giá trị nhỏ nhất của môđun của z là
Cho số phức z thỏa mãn: |z− + 1 - i| = |z|
Đặt z = a + bi (a, b ∈ R) . Ta có: z− + 1 - i = a - bi + 1 - i = a + 1 - (b + 1)i
Từ giả thiết ta có :
(a + 1)2 + (b + 1)2 = a2 + b2 ⇔ a2 + 2a + 1 + b2 + 2b + 1 = a2 + b2
⇔ 2a + 2b + 2 = 0 ⇔ a + b + 1 = 0 ⇔ b = -1 - a
Khi đó |z|2 = a2 + b2 = a2 + ( -1 - a)2 = 2a2 + 2a + 1
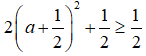
Từ đó suy ra môđun của z nhỏ nhất bằng 1/√2
Câu 37: Biết rằng logMN = logNM và N ≠ . Tính giá trị của MN.
A. -1 B. 1 C. 2 D. 10
logMN = logNM
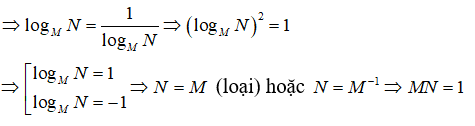
Câu 38: Biết:
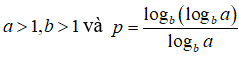
Khi đó ap bằng
A. logab B. alogba C. logba D. b
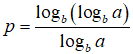
plogba = logb(logba) => logbap = logb(logba)
=> ap = logba
Câu 39: Giả sử x là nghiệm của phương trình logx25 - logx4 = logx√x.
Điều kiện 9 < x ≠ 1
logx25 - logx4 = logx√x
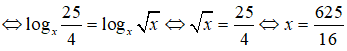
Câu 40: Điện tích (tính bằng culông) được tích trong các tấm của một tụ điện bị rò sau thời gian t giây được xác đinh bởi công thức Q(t) = Q0.(1,122)-1 trong đó Q0 là điện tích ban đầu. Sau bao lâu thì điện tích trong tụ còn một nửa (làm tròn kết quả đến hàng đơn vị)?
A. 5 giây B. 6 giây C. 8 giây D. 10 giây.
Khi điện tích trong tụ còn một nửa thì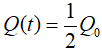 
Ta có:
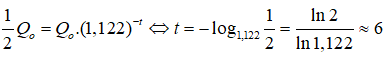
Câu 41: Tìm tập nghiệm của bất phương trình
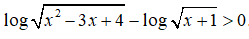
A. (1; 3) B. (-1; 3) C. (-1; 1) ∪ (3; +∞) D. (-∞; 1) ∪ (3; +∞)
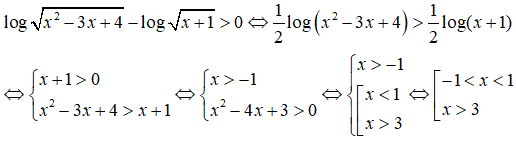
Câu 42: Tìm tập nghiệm của bất phương trình
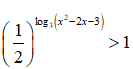
A. (1 - √5; 1 + √5) B. (1 - √5; -1) ∪ (3; 1 + √5)
C. (-1; -√5; -1) ∪ (3; 1 + √5) D. (-∞; 1 - √5) ∪ (1 + √5; +∞)
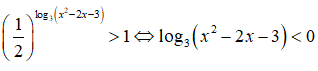
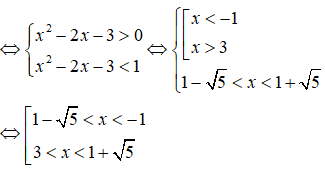
Câu 43:
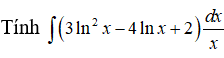
A. ln3x - 2ln2x + 2lnx + C B. -ln3x - 2ln2x + 2lnx + C
C. ln3x + 2ln2x + 2lnx + C D. ln3x - 2ln2x - 2lnx + C
Đặt t = lnx, suy ra dt = dx/x
I = ∫(3t2 - 4t + 2)dt = t3 - 2t2 + 2t + C = ln3x - 2lnxx + 2lnx + C
Câu 44: Hàm số F(x) = ln|sinx - 3cosx| là một nguyên hàm của hàm số nào trong các hàm số sau đây?
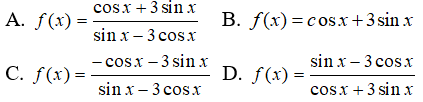
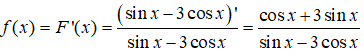
Câu 45: Tính ∫x2.sinxdx
A. -x2cosx + 2x.sinx - 2cosx + C B. x2sinx + 2x.cosx - 2sinx + C
C. -x2cosx + 2x.sinx + 2cosx + C D. 2x.cosx + sinx + C
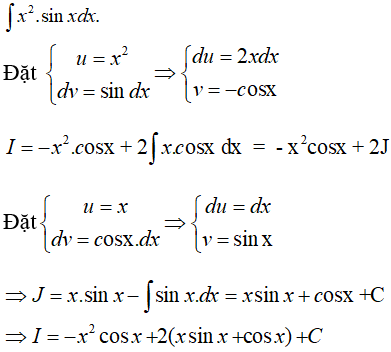
Câu 46: Cho tích phân
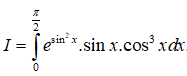
Nếu đổi biến số t = sin2x thì:
