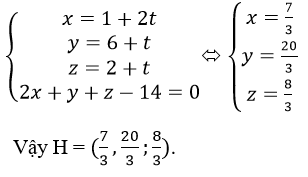Cho bốn điểm A(1, 6, 2), B(4, 0, 6); C(5, 0, 4), D(5, 1, 3). Chứng minh rằng bốn điểm đó

Ôn tập chương 3

Haylamdo biên soạn và sưu tầm lời giải Bài 1 trang 109 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 1 (trang 109 sgk Hình Học 12 nâng cao): Cho bốn điểm A(1, 6, 2), B(4, 0, 6); C(5, 0, 4), D(5, 1, 3).

a) Chứng minh rằng bốn điểm đó không đồng phẳng.

b) Tính thể tích tứ diện ABCD.

c) Viết phương trình mp(BCD)

d) Viết phương trình mặt cầu tâm A tiếp xúc với mp(BCD). Tìm tọa độ tiếp điểm.

Lời giải:

a) Ta có: AB→=(3,-6,4);AC→=(4,-6,2),AD→=(4,-5,1) nên [AB→;AC→ ] = (12; 10; 6) và [AB→.AC→ ].AD→=4 ≠ 0. Suy ra A, B, C, D không đồng phẳng.

b) Thể tích tứ diện ABCD là:

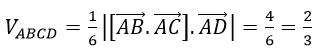
c) Mặt phẳng (BCD) là mặt đi qua B(4, 0, 6) và nhận vectơ [BC→;BD→] là vectơ pháp tuyến.

Ta có BC→=(1,0,-2);BD→=(1,1,-3), suy ra [BC→;BD→ ]=(2,1,1) nên mp(BCD) có phương trình là:

2(x-4)+y+(z-6)=0 <=> 2x+y+z-14=0

d) Mặt cầu tâm A(1, 6, 2) tiếp xúc với mp(BCD) có bán kính là

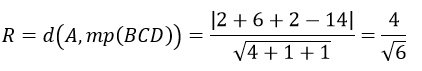
Nên mặt cầu có phương trình là: (x-1)²+(y-6)²+(z-2)²=8/3

Tiếp điểm H của mặt cầu với mp(BCD) chính là hình chiếu vuông góc của tâm A(1, 6, 2) lên mp(BCD)

Để tìm tọa độ điểm H trước hết ta viết phương trình đường thẳng Δ đi qua A và Δ ⊥ (BCD))

Δ đi qua A(1, 6, 2) và nhận vectơ pháp tuyến của mp(BCD) là n→=(2,1,1)là vectơ chỉ phương, nên Δ có phương trình

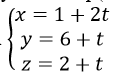
Khi đó H là giao điểm của Δ và mp(BCD), nên tọa độ của H là nghiệm của hệ