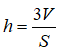Cho tọa độ bốn đỉnh của một hình tứ diện, làm thế nào để tìm: Tọa độ trọng tâm tứ diện

Ôn tập chương 3

Haylamdo biên soạn và sưu tầm lời giải Bài 2 trang 108 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 2 (trang 108 sgk Hình Học 12 nâng cao): Cho tọa độ bốn đỉnh của một hình tứ diện, làm thế nào để tìm:

a) Tọa độ trọng tâm tứ diện;

b) Tọa độ của tâm và bán kính mặt cầu ngoại tiếp tứ diện;

c) Thể tích tứ diện

d) Độ dài tứ đường cao ứng với một mặt tứ diện?

Lời giải:

Cho tứ diện ABCD có A=(x_A,y_A,z_A), B=(x_B;y_B,z_B); C=(x_C,y_C,z_C), D = (x_D,y_D,z_D)

a) Tọa độ trọng tâm tứ diện là:

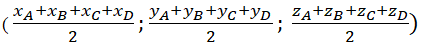
b) Gọi I = (x₀;y₀;z₀) là tâm mặt cầu ngoại tiếp tứ diện ABCD, ta có:

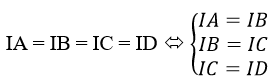
Giải hệ ta tìm được tọa độ (x₀;y₀;z₀) của tâm mặt cầu ngoại tập tứ diện ABCD.

Từ đó, tính được bán kính mặt cầu ngoại tiếp tứ diện ABCD là

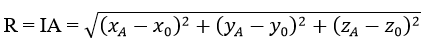
c) Thể tích tứ diện ABCD là

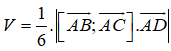
d) Độ dài đường cao ứng với mỗi mặt của tứ diện là:

trong đó S là diện tích đáy ứng với chiều cao h.