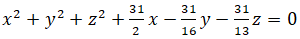Cho hai đương thẳng: trang 110 sgk Hình Học 12 nâng cao

Ôn tập chương 3

Haylamdo biên soạn và sưu tầm lời giải Bài 6 trang 110 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 6 (trang 110 sgk Hình Học 12 nâng cao): Cho hai đường thẳng:

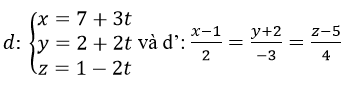
a) Chứng minh rằng d và d’ đồng phẳng. viết phương trình mặt phẳng (P) chứa chúng.

b) Tính thể tính hình tứ diện giới hạn bởi mp(P) và ba mặt phẳng tọa độ.

c) Viết phương trình mặt cầu ngoại tiếp tứ diện nói trên.

Lời giải:

a) Đường thẳng d đi qua M(7; 2; 1) và có vectơ chỉ phương u→=(3;2; -2) d’ đi qua M’(1; -2; 5) và có vectơ chỉ phương u'→=(2; -3;4)

Ta có [u→,u'→ ]=(2; -16; -13), MM'→=(-6; -4;4)

Mặt phẳng (P) chứa d và d’ có vectơ pháp tuyến là [u→,u'→ ]=(2; -16; -13) đi qua (P) đi qua M(7; 2; 1) ∈d nên (P) có phương trình là:

2(x-7)-16(y-2)-13(z-1)=0 <=> 2x-16y-13z+31=0

b) Mặt phẳng (P) cắt Ox tại A(-31/2;0;0); cắt Oy tại B(0;31/16;0); cắt Oz tại C(0;0;31/13). Suy ra thể tích tứ diện cần tìm là:

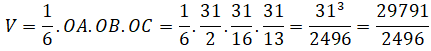
c) Viết phương trình mặt cầu đi qua 4 điểm O, A, B, C.

Gọi phương trình mặt cầu là: x²+y²+z²+ax+by+cz+d=0

Vì mặt cầu đi qua O(0; 0; 0) nên d = 0’

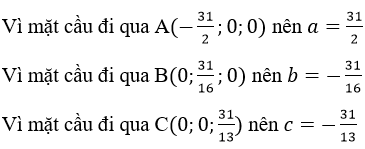
Vậy phương trình mặt cầu là: