Cho hai mặt phẳng (P) và (Q) lần lượt có phương trình: (P): 2x-y+z+2=0 và (Q): x+y+2z-1=0

Ôn tập chương 3

Haylamdo biên soạn và sưu tầm lời giải Bài 8 trang 111 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 8 (trang 111 sgk Hình Học 12 nâng cao): Cho hai mặt phẳng (P) và (Q) lần lượt có phương trình:

(P): 2x-y+z+2=0 và (Q): x+y+2z-1=0

a) Chứng minh rằng (P) và (Q) cắt nhau. Tìm góc giữa hai mặt phẳng đó.

b) Viết phương trình đường thẳng d đi qua A(1; 2; -3), song song với cả (P) và (Q).

c) Viết phương trình mp (R) đi qua B(-1; 3; 4), vuông góc với cả (P) và (Q).

Lời giải:

a) Mp(P) có vectơ pháp tuyến n₁→=(2; -1;1)

Mp(Q) có vectơ pháp tuyến n₂→=(1;1;2)

Ta có: [n₁→,n²→]=(-3; -3;3) ≠ 0→ , vậy (P) và (Q) cắt nhau.

Ta có

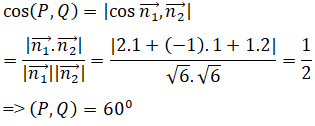
b) Đường thẳng d đi qua A(1; 2; -3) và song song với cả (P) và (Q) là đường thẳng đi qua A(1; 2; -3) và nhận[n₁→,n₂→]=(-3; -3;3) là, vectơ chỉ phương, vậy phương trình của d là:

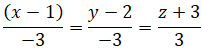
c) Mặt phẳng (R ) đi qua B(-1, 3, 4) và vuông góc với cả (P) và (Q) là mặt phẳng đi qua B(-1; 3; 4) và nhận[n₁→,n₂→ ]=(-3; -3;3) làm vectơ pháp tuyến.

Vậy (R ) có phương trình là: -3(x+1)-3(y-3)+3(z-4)=0

<=> x+y-z+2=0