Cho mặt cầu (S) có phương trình: x2+y2+z2-2x-4y-6z=0

Ôn tập chương 3

Haylamdo biên soạn và sưu tầm lời giải Bài 9 trang 111 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 9 (trang 111 sgk Hình Học 12 nâng cao): Cho mặt cầu (S) có phương trình: x₂+y₂+z₂-2x-4y-6z=0

a) Tìm tọa độ tâm mặt cầu và tính bán kính mặt cầu.

b) Tùy theo giá trị của k, xét vị trị tương đối của mặt cầu (S) và mp(P) với (P): x+y-z+k=0

c) Mặt cầu cắt ba trục Ox, Oy, Oz lần lượt tại ba diểm A, B, C khác với gốc tọa độ O. Viết phương trình mp(ABC).

d) Viết phương trình mặt phẳng tiếp xúc với mặt cầu (S) tại điểm B.

e) Viết phương trình mặt phẳng tiếp xúc với mặt cầu (S) và song song với mặt phẳng (Q): 4x+3y-12z-1=0

Lời giải:

a) phương trình: x²+y²+z²-2x-4y-6z=0

⇔ (x-1)²+(y-2)²+(z-3)²=14

Vậy mặt cầu (S) có tâm là I = (1; 2; 3), bán kính R = √14

b) Tính khoảng cách từ tâm I(1; 2; 3) của mặt cầu (S) đến mặt phẳng (P) là:

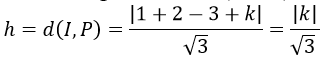
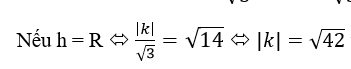
thì (P) là mặt phẳng tiếp xúc với mặt cầu.

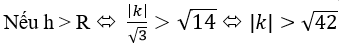
thì mp(P) và mặt cầu (S) không có điểm chung.

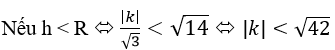
thì mp(P) cắt mặt cầu (S)

c) phương trình giao điểm của mặt cầu (S) và trục Ox là:

⇒ Mặt cầu (S) cắt trục Ox tại A(2; 0; 0) và O(0; 0; 0)

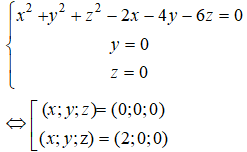
Tương tự, (S) cắt trục Oy tại B(0; 4; 0) và O(0; 0; 0)

(S) cắt trục Oz tại C(0; 0; 6) và O(0; 0; 0)

Vậy mặt phẳng (ABC) có phương trình:

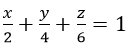
d) Mặt phẳng tiếp xúc với mặt cầu (S) tại điểm B(0; 4; 0) là mặt phẳng đi qua B(0; 4; 0) và có vectơ pháp tuyến là BI→=(1; -2;3), vậy phương trình của mặt phẳng đó là: (x-0)-2(y-4)+3(z-0)=0 <=> x-2y+3z+8=0

e) Vì mặt phẳng cần tìm song song với mp(Q): 4x+3y-12z-1=0 nên có dạng: 4x+3y-12z+D=0 (α)

Vì mặt tiếp xúc với mặt cầu (S) nên ta có:

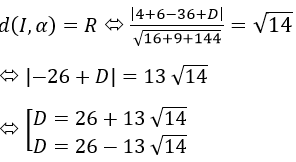
Vậy mặt phẳng cần tìm có phương trình là: 4x+3y-12z+26+13√14=0 hoặc 4x+3y-12z+26-13√14=0