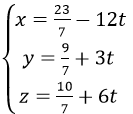Cho hai điểm A(1, -1, -2); B(3,1, 1) và mp (P): x-2y+3z-5=0

Ôn tập chương 3

Haylamdo biên soạn và sưu tầm lời giải Bài 2 trang 109 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 2 (trang 109 sgk Hình Học 12 nâng cao): Cho hai điểm A(1, -1, -2); B(3,1, 1) và mp(P): x-2y+3z-5=0

a) Tìm tọa độ điểm A’ đối xứng với A qua mp(P).

b) Tìm góc giữa đường thẳng AB và mp(P).

c) Viết phương trình mp(Q) đi qua A, B và vuông góc với mp(P).

d) Tìm tọa độ giao điêm I của đường thẳng AB và mp(P). viết phương trình đường thẳng Δ nằm trong (P), đi qua I và vuông góc với AB.

Lời giải:

a) + Viết phương trình đường thẳng d đi qua A và (d) ⊥ mp(P).

Đường thẳng (d) đi qua A(1, -1, -2) và nhận vectơ pháp tuyến của mp(P) là n→=(1,-2,3) là vectơ chỉ phương, nên đường thẳng (d) có phương trình

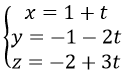
+ Tìm tọa độ giao điểm H của d và mp(P)

Tọa độ của H là nghiệm của hệ:

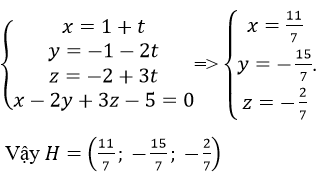
+ Vì A và A’ đối xứng với nhau qua mp(P) nên H chính là trung điểm của AA’, ta có:

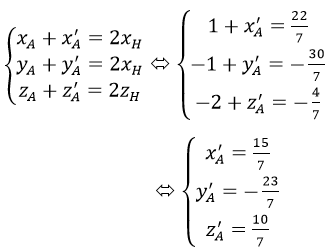
b) Ta có AB→ =(2,2,3), vectơ pháp tuyến của mp(P) là n→=(1,-2,3) nên góc giữa AB và mp(P) xác định như sau:

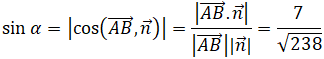
c) Mặt phẳng (Q) đi qua AB vuông góc với mp(P) là mặt phẳng đi qua A(1, -1, -2) và nhận vectơ [AB→,n→ ]=(12,-3,-6) làm vectơ pháp tuyến, nên mp(Q) có phương trình là:

12(x-1)-3(y+1)-6(z+2)=0 <=> 4x-y-2z-9=0

d) Đường thẳng AB có phương trình:

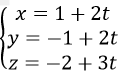
nên tọa độ giao điểm I của đường thẳng AB và mp(P) là nghiệm của hệ

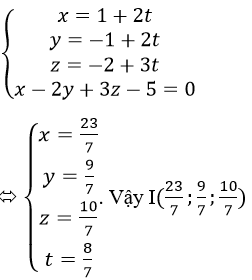
Vì đường thẳng Δ nằm trong mp(P) và Δ ⊥ AB nên Δ nhận vectơ u→=[n→,AB→] làm vectơ chỉ phương, với AB→=(2,2,3), n→=(1,-2,3) là vectơ pháp tuyến của mp(P).

Ta tính được u→=[n→,AB→ ]=(-12,3,6)

Nên phương trình của đường thẳng Δ là