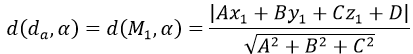Bằng phương pháp tọa độ, làm thế nào để tính khoảng cách: a) Từ một điểm đến một mặt phẳng

Ôn tập chương 3

Haylamdo biên soạn và sưu tầm lời giải Bài 7 trang 109 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.

Bài 7 (trang 109 sgk Hình Học 12 nâng cao): Bằng phương pháp tọa độ, làm thế nào để tính khoảng cách:

a) Từ một điểm đến một mặt phẳng.

b) Từ một điểm đén một đường thẳng

c) Giữa hai đường chéo nhau.

d) Giữ hai đường thẳng song song

e) Giữa hai mặt song song.

f) Giữa đường và mặt phẳng song song với đường thẳng đó.

Lời giải:

Cho điểm A(x₀,y₀,z₀),mp(α):Ax+By+Cz+D=0;

Đường thẳng

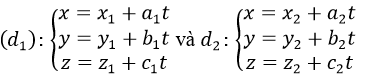
a) Khoảng cách từ điểm A đến mp(α) được xác định như sau:

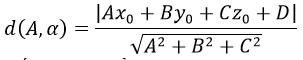
b) Khoảng cách từ điểm A đến đường thẳng (d₁) là:

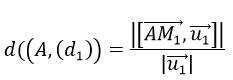
Trong đó M₁ (x₁,y₁,z₁) là điểm trên (d₁ ),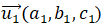 là vectơ chỉ phương của d₁.

c) Giả sử d₁ và d₂ chéo nhau, khi đó khoảng cách giữa hai đường thẳng d₁ và d₂ là:

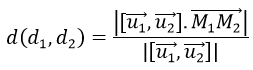
Trong đó M₁∈d₁và u₁→ là vectơ chỉ phương của d₁

M₂ ∈d₂và u₂→ là vectơ chỉ phương của d₂

d) Giả sử d₁ và d₂ song song với nhau, khi đó cách từ d₁ đến d₂ là khoảng cách từ 1 điểm trên d₁ đến đường thẳng d₂, chẳng hạn:

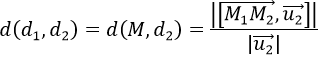
Trong đó M₁∈d₁,M₂∈d₂,u₂→ là vectơ chỉ phương của đường thẳng d₂.

e) Cho hai mặt phẳng (α) và (β) song song với nhau, khi đó khoảng cách giữa (α)và (β) là khoảng cách từ một điểm M bất kì thuộc (β)đến (α).

Chẳng hạn, M(x₀,y₀,z₁0 )∈(β)và (α):Ax+By+Cz+D=0

Khi đó

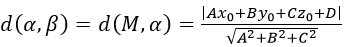
f) Giả sử đường thẳng d₁ song song với mặt phẳng (α):Ax+By+Cz+D=0. Khi đó khoảng cách từ d₁ đến mặt phẳng (α) là khoảng cách từ 1 điểm M bất kì thuộc d₁ đến mp(α)

Chẳng hạn M₁ (x₁,y₁,z₁ )∈d₁, khi đó ta có: