Bằng Phương pháp tọa đố, làm thế nào để xác định được vị trí tương đối. a) Giữa hai mặt phẳng?
Ôn tập chương 3
Haylamdo biên soạn và sưu tầm lời giải Bài 6 trang 108 sgk Hình Học 12 nâng cao được biên soạn lời giải chi tiết sẽ giúp bạn biết cách làm bài tập môn Toán 12.
Bài 6 (trang 108 sgk Hình Học 12 nâng cao): Bằng Phương pháp tọa đố, làm thế nào để xác định được vị trí tương đối.
a) Giữa hai mặt phẳng?
b) Giữa hai đường thẳng?
Lời giải:
a) Cho hai mặt phẳng có phương trình (P): Ax+By+Cz+D=0
(Q): A'x + B'y+C'z + D'=0
Khi đó, (P) cắt (Q) <=> A: B: C ≠ A’: B’: C’
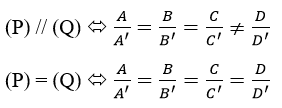
Chú ý: A: B: C ≠ A’: B’: C’ khi và chỉ khi có ít nhất hai trong ba tỉ số:
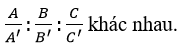
b) Cho 2 đường thẳng d1 đi qua M1(x1,y1,z1) và vectơ chỉ phương u1→(a1,b1,c1) và d2 đi qua M2 (x2,y2,z2) và vectơ chỉ phương u1→(a2,b2,c2)
Khi đó, +) d1 và d2 chéo nhau <=> u1→,u2→,M1M2→ không đồng phẳng
<=> [u1→,u2→].M1M2→ ≠ 0

Chú ý: chúng ta có thể xét vị trí tương đối của hai đường thẳng bằng cách xét số nghiệm của hệ phương trình gồm hai phương trình của hai đường thẳng.
+ Nếu hệ có 1 nghiệm thì đường thẳng cắt nhau.
+ Nếu có vô số nghiệm thì hai đường thẳng song song (nếu đồng phẳng) hoặc chéo nhau.

