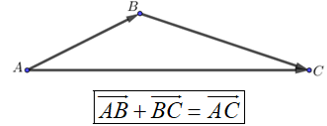
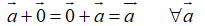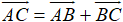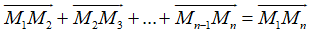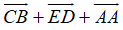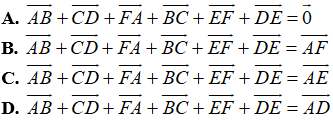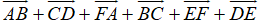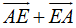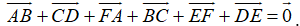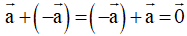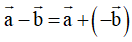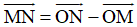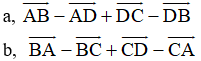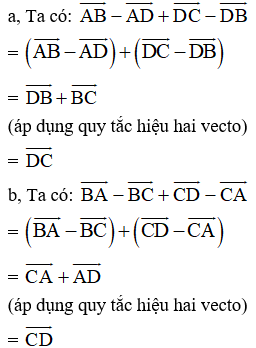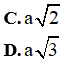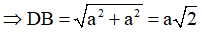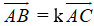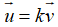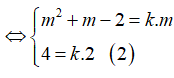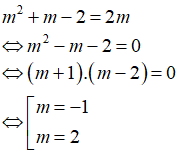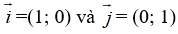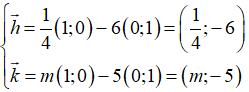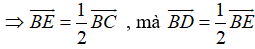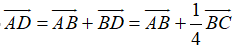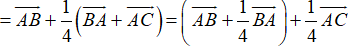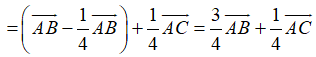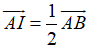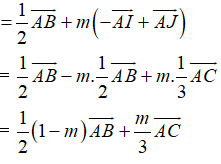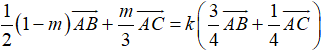Các dạng bài tập Vecto lớp 10 (chọn lọc, có lời giải)

---

Tổng hợp các dạng bài tập Vecto Toán lớp 10 sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều với phương pháp giải chi tiết và bài tập đa dạng giúp học sinh ôn tập, biết cách làm bài tập vectơ.

Các dạng bài tập Vecto lớp 10 (chọn lọc, có lời giải)

• Xác định vectơ. Tìm điểm đầu, điểm cuối, giá của vectơ

• Tính độ dài của vectơ

• Tìm các vectơ cùng phương, cùng hướng, ngược hướng

• Chứng minh hai vectơ bằng nhau, hai vectơ đối nhau

• Tìm tổng của hai hay nhiều vectơ

• Tìm hiệu của hai vectơ

• Chứng minh đẳng thức vectơ

• Tính độ dài của tổng và hiệu hai hay nhiều vectơ

• Xác định các điểm thỏa mãn đẳng thức vectơ

• Tính độ dài vectơ khi biết tích vectơ với một số

• Tìm một điểm thỏa mãn một đẳng thức vectơ cho trước

• Chứng minh đẳng thức vectơ

• Phân tích một vectơ thành hai hay nhiều vectơ cho trước

• Chứng minh hai vectơ cùng phương

• Chứng minh ba điểm thẳng hàng

• Xác định góc giữa hai vectơ

• Cách tính tích vô hướng của hai vectơ

• Tính độ dài đoạn thẳng, độ dài vectơ

• Chứng minh hai vectơ hay hai đường thẳng vuông góc

• Chứng minh đẳng thức về tích vô hướng của vectơ hoặc về độ dài đoạn thẳng

• Tính công sinh bởi một lực thỏa mãn các điều kiện cho trước

---

---

---

Lưu trữ: Các dạng bài tập Vecto (sách cũ)

• Hai vecto cùng phương, hai vecto cùng hướng hay, chi tiết Xem chi tiết
• Bài tập về tổng của hai vecto (cực hay, chi tiết) Xem chi tiết
• Bài tập về hiệu của hai vecto (cực hay, chi tiết) Xem chi tiết
• Bài tập về Quy tắc hình bình hành của vecto (cực hay, chi tiết) Xem chi tiết
• Bài tập về Quy tắc trung điểm của vecto (cực hay, chi tiết) Xem chi tiết
• Bài tập về Quy tắc trọng tâm tam giác của vecto (cực hay, chi tiết) Xem chi tiết
• Cách phân tích một vecto theo hai vecto không cùng phương (cực hay, chi tiết) Xem chi tiết
• Bài tập Tọa độ của vecto, tọa độ của một điểm (cực hay, chi tiết) Xem chi tiết
• Tìm m để hai vecto cùng phương (cực hay, chi tiết) Xem chi tiết
• Cách tìm tọa độ trung điểm của đoạn thẳng (cực hay, chi tiết) Xem chi tiết
• Cách tìm tọa độ của trọng tâm tam giác (cực hay, chi tiết) Xem chi tiết
• Tìm tọa độ điểm thỏa mãn điều kiện cho trước (cực hay, chi tiết) Xem chi tiết

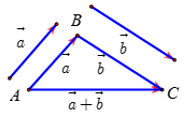
Bài tập về tổng của hai vecto

A. Phương pháp giải

Định nghĩa: Cho hai vecto . Lấy một điểm A tùy ý ta vẽ , từ B vẽ . Vecto được gọi là tổng của hai vecto . Kí hiệu: . Phép toán tìm tổng của hai vecto còn được gọi là phép cộng hai vecto.

Các tính chất:

Tính chất giao hoán:

Tính chất kết hợp:

Tính chất vecto-không:

Các quy tắc:

Quy tắc 3 điểm: Cho 3 điểm A, B, C tùy ý ta có:

Quy tắc n điểm (mở rộng quy tắc 3 điểm): Cho n điểm , ta có:

(quy tắc này được dùng để tìm tổng của nhiều vecto nối đuôi nhau)

Phương pháp giải: Sử dụng linh hoạt các quy tắc và tính chất của phép cộng vecto để giải quyết bài tập.

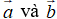
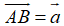
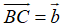
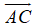
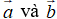
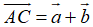
B. Ví dụ minh họa

Ví dụ 1: Ví dụ 1. Cho 5 điểm A, B, C, D, F. Chứng minh rằng

Hướng dẫn giải:

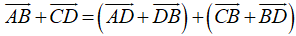
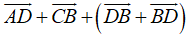
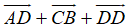
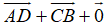
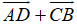
a, Ta có: (áp dụng quy tắc 3 điểm)

= (tính chất giao hoán kết hợp)

= (quy tắc 3 điểm)

= (nhớ lại khái niệm vecto-không là vecto có điểm đầu và điểm cuối trùng nhau)

= (tính chất vecto-không)

Vậy 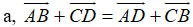(đpcm)

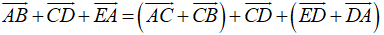
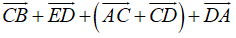
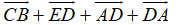
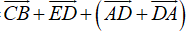
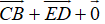
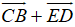
b, Ta có: (áp dụng quy tắc 3 điểm)

= (áp dụng tính chất giao hoán và kết hợp)

= (quy tắc 3 điểm)

= (tính chất kết hợp)

=

= (vecto có điểm đầu và điểm cuối trùng nhau là vecto-không)

= (tính chất vecto-không)

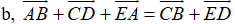
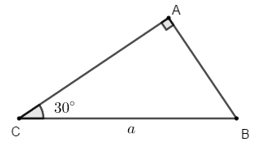
Vậy (đpcm).

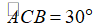
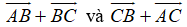
Ví dụ 2: Ví dụ 2. Cho tam giác ABC vuông tại A có và BC = a. Tính độ dài vecto .

Hướng dẫn giải:

Nhận xét: để làm bài tập này, ta cần nhớ lại công thức độ dài vecto:

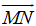
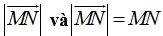
Độ dài của vecto , ký hiệu là .

Ví dụ 3: Ví dụ 3. Cho 6 điểm A, B, C, D, E, F. Đẳng thức nào sau đây đúng?

Hướng dẫn giải:

Ta có:

= (tính chất giao hoán và kết hợp)

= (quy tắc 3 điểm)

=

= .

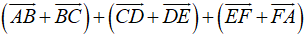
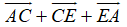
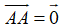
Vậy

Suy ra A đúng, B, C, D sai.

Đáp án A

Bài tập về hiệu của hai vecto

A. Phương pháp giải

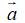
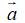
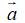
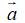
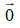
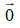
Vecto đối của một vecto: Vecto đối của vecto là vecto ngược hướng với và có cùng độ dài với vecto , ký hiệu là -

Vecto đối của vecto là vecto .

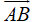
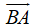
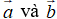
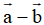
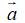
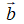
Vecto đối của vecto là vecto .

Hiệu hai vecto: Hiệu của hai vecto , kí hiệu là , là tổng của vecto và vecto đối của vecto , tức là

Phép lấy hiệu của hai vecto được gọi là phép trừ hai vecto.

Quy tắc về hiệu hai vecto: Nếu là một vecto đã cho thì với điểm O bất kỳ, ta luôn có

Phương pháp giải: áp dụng quy tắc về hiệu hai vecto, quy tắc ba điểm, vecto đối…

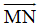
B. Ví dụ minh họa

Ví dụ 1: Cho 4 điểm A, B, C, D phân biệt. Chứng minh rằng

Hướng dẫn giải:

Ta có: 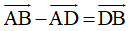(1) (áp dụng quy tắc về hiệu hai vecto)

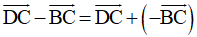
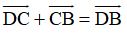
Lại có: (vecto đối)

(2) (áp dụng quy tắc ba điểm về tổng hai vecto)

Từ (1) và (2) suy ra: 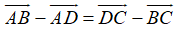(đpcm)

Ví dụ 2: Cho tứ giác ABCD, tìm các vecto sau

Hướng dẫn giải:

Ví dụ 3: Cho hình vuông ABCD có cạnh là a. Độ dài của vecto 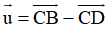là

A. a

B. 2a

Hướng dẫn giải:

Ta có: 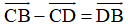(quy tắc về hiệu hai vecto)

Suy ra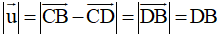

ABCD là hình vuông cạnh với đường chéo DB

Vậy độ dài vecto .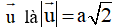

Đáp án C

Tìm m để hai vecto cùng phương

A. Phương pháp giải

• Áp dụng điều kiện để hai vecto cùng phương để giải bài tập dạng này.

Điều kiện cần và đủ để hai vecto ( # 0) cùng phương là có một số k để .

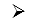
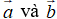
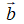
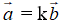
Nhận xét: Ba điểm phân biệt A, B, C thẳng hàng khi và chỉ khi có số k khác 0 để

• Áp dụng trong hệ tọa độ:

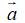
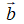
Cho = (a₁; a₂) và = (b₁; b₂), với b₁; b₂ # 0

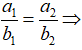
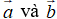
Khi đó nếu có: cùng phương.

B. Ví dụ minh họa

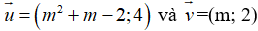
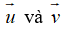
Ví dụ 1: Cho . Tìm m để hai vecto cùng phương.

Hướng dẫn giải:

Để hai vecto 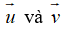cùng phương tồn tại số k thỏa mãn

Từ (2) suy ra k = 2 thay vào (1) ta được:

Vậy m = -1 và m = 2 thì hai vecto 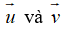cùng phương.

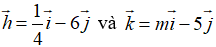
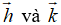
Ví dụ 2: Cho hai vecto . Tìm m để hai vecto cùng phương.

Hướng dẫn giải:

Ta có 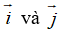là các vecto đơn vị với

Suy ra

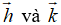
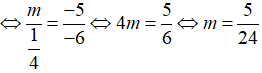
Hai vecto cùng phương

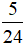
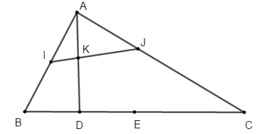
Vậy m = thì thỏa mãn yêu cầu bài toán.

Ví dụ 3: Cho tam giác ABC có E là trung điểm của BC, I là trung điểm của AB. Gọi D, J, K lần lượt là các điểm thỏa mãn 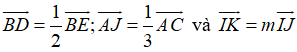. Tìm m để A, K, D thẳng hàng.

Hướng dẫn giải:

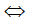
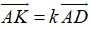
Ba điểm A, K, D thẳng hàng tồn tại k để (1)

Ta phân tích các vecto 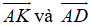theo hai vecto

+ E là trung điểm của BC

Suy ra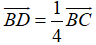

Ta có

Do đó 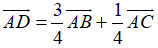(2)

+ Lại có: I là trung điểm AB

Ta có: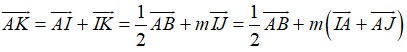

Do đó 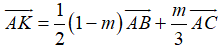(3)

Từ (1), (2) và (3) suy ra

Vậy m = thì ba điểm A, K, D thẳng hàng.