15 Bài tập Tổng và hiệu của hai vectơ (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 10
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Tổng và hiệu của hai vectơ Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
15 Bài tập Tổng và hiệu của hai vectơ (có đáp án) - Kết nối tri thức Trắc nghiệm Toán 10
Câu 1. Quy tắc ba điểm được phát biểu:
A. Với ba điểm bất kì A, B, C ta có ;
B. Với ba điểm bất kì A, B, C ta có ;
C. Với ba điểm bất kì A, B, C ta có ;
D. Với ba điểm bất kì A, B, C ta có .
Câu 2. Cho tam giác ABC có I là trung điểm cạnh AB và G là trọng tâm tam giác ABC. Đẳng thức nào sau đây sai:
A. ;
B. ;
C. ;
D. .
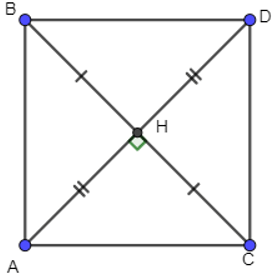
Câu 3. Cho tam giác ABC vuông cân tại A, đường cao AH và BC = 10cm. Tính độ dài vectơ .
A. 5cm;
B. 10dm;
C. 10cm;
D. 15cm.
Câu 4. Vectơ đối của vectơ - không là:
A. Mọi vectơ khác vectơ - không;
B. Không có vectơ nào ;
C. Chính nó;
D. Mọi vectơ kể cả vectơ – không.
Câu 5. Cho hình bình hành ABCD có một điểm O bất kì. Đẳng thức nào sau đây đúng?
A. ;
B. ;
C. ;
D. .
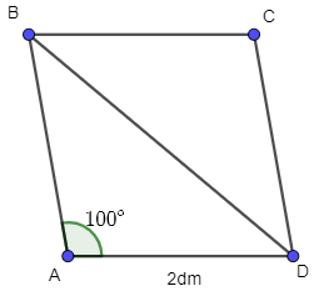
Câu 6. Cho hình thoi ABCD có độ dài cạnh bằng 2 dm và . Tính độ dài vectơ .
A. 9,39 dm;
B. 3,06 dm;
C. 7,31 dm;
D. 2,70 dm.
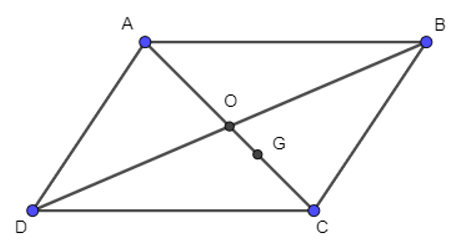
Câu 7. Cho hình bình hành ABCD có tâm O, G là trọng tâm tam giác BCD. Đẳng thức nào sau đây sai?
A. ;
B. ;
C. ;
D. .
Câu 8. Tính tổng
A. ;
B. ;
C. ;
D. .
Câu 9. Cho hình bình hành ABCD. Hãy tìm điểm M để .
A. M là một điểm bất kì;
B. M là điểm thỏa mãn ACMD là hình bình hành;
C. M là điểm thỏa mãn ACDM là hình bình hành;
D. Không tồn tại điểm M.
Câu 10. Cho hình bình hành ABCD tâm O. Ba điểm M, N, P thỏa mãn:
+) ;
+);
+) .
Nhận xét nào sau đây đúng về M, N, P.
A. M là trung điểm của đoạn thẳng NP;
B. N là trung điểm của đoạn thẳng MP;
C. P là trung điểm của đoạn thẳng MN;
D. Cả A, B, C đều sai.
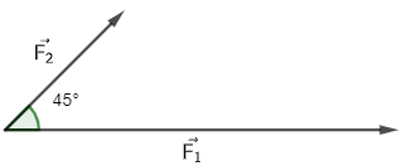
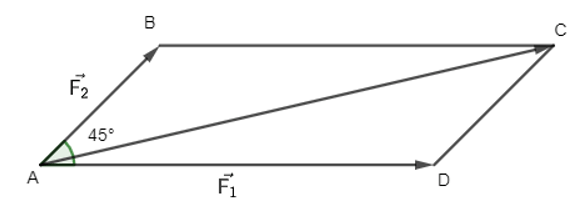
Câu 11. Hai lực cùng tác động lên một vật, cho . Tính độ lớn của hợp lực (biết góc giữa bằng 45°).
A. 10N;
B. 4N;
C. 5,32N;
D. 9,36N.
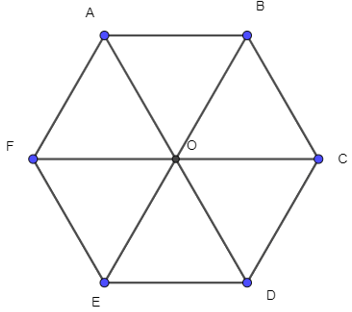
Câu 12. Cho lục giác đều ABCDEF và O là tâm. Có bao nhiêu đẳng thức dưới đây là đẳng thức đúng?
1. ;
II. ;
III. ;
IV. .
A. 1;
B. 2;
C. 3;
D. 4.
Đáp án đúng là A
+) Ta có . Do đó A sai.
+) Ta có . Do đó B đúng.
+) Ta có . Do đó C sai.
+) Ta có . Do đó D sai.
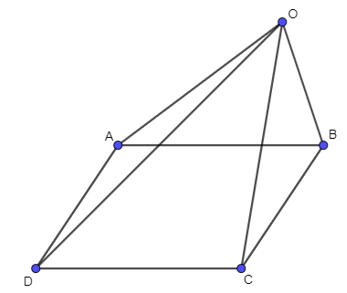
Câu 13. Hai người cùng kéo một con thuyền với hai lực có độ lớn lần lượt là 550 N, 800 N. Cho biết góc giữa hai vectơ là 52o.
Độ lớn của vectơ hợp lực là tổng của hai lực và nằm trong khoảng nào dưới đây?
A. (900; 1 000);
B. (1 000; 1 100);
C. (1 100; 1 200);
D. (1 200; 1 300).
Câu 14. Cho hình vuông ABCD có cạnh bằng 1. So sánh độ dài của hai vectơ sau:
;
.
A. ;
B. ;
C. ;
D. .
Câu 15. Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn: ; ; . Tính độ dài các vectơ .
A. ;
B. a;
C. ;
D. a
Câu 1:
Quy tắc ba điểm được phát biểu:
A. Với ba điểm bất kì A, B, C ta có \(\overrightarrow {AB} + \overrightarrow {AC} = \overrightarrow {BC} \);
B. Với ba điểm bất kì A, B, C ta có \(\overrightarrow {AB} + \overrightarrow {CB} = \overrightarrow {AC} \);
C. Với ba điểm bất kì A, B, C ta có \(\overrightarrow {AB} + \overrightarrow {CA} = \overrightarrow {BC} \);
D. Với ba điểm bất kì A, B, C ta có \(\overrightarrow {AB} + \overrightarrow {BC} = \overrightarrow {AC} \).
Câu 2:
Cho tam giác ABC có I là trung điểm cạnh AB và G là trọng tâm tam giác ABC. Đẳng thức nào sau đây sai:
A. \(\overrightarrow {IA} + \overrightarrow {IB} = \overrightarrow {AB} \);
B. \(\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \);
C. \(\overrightarrow {IA} = - \overrightarrow {IB} \);
D. \(\overrightarrow {BA} + \overrightarrow {AC} = \overrightarrow {BC} \).
Câu 3:
Cho tam giác ABC vuông cân tại A, đường cao AH và BC = 10cm. Tính độ dài vectơ \(\overrightarrow {AB} + \overrightarrow {AC} \).
A. 5cm;
B. 10dm;
C. 10cm;
D. 15cm.
Câu 4:
Vectơ đối của vectơ - không là:
A. Mọi vectơ khác vectơ - không;
B. Không có vectơ nào ;
C. Chính nó;
D. Mọi vectơ kể cả vectơ – không.
Câu 5:
Cho hình bình hành ABCD có một điểm O bất kì. Đẳng thức nào sau đây đúng?
A. \(\overrightarrow {OA} - \overrightarrow {OB} = \overrightarrow {OC} - \overrightarrow {OD} \);
B. \(\overrightarrow {OB} - \overrightarrow {OA} = \overrightarrow {OC} - \overrightarrow {OD} \);
C. \(\overrightarrow {OA} - \overrightarrow {OD} = \overrightarrow {OC} - \overrightarrow {OB} \);
D. \(\overrightarrow {OA} - \overrightarrow {OC} = \overrightarrow {OD} - \overrightarrow {OB} \).
Câu 6:
Cho hình thoi ABCD có độ dài cạnh bằng 2 dm và \(\widehat {BAD} = 100^\circ \). Tính độ dài vectơ \(\overrightarrow {DA} + \overrightarrow {DC} \).
A. 9,39 dm;
B. 3,06 dm;
C. 7,31 dm;
D. 2,70 dm.
Câu 7:
Cho hình bình hành ABCD có tâm O, G là trọng tâm tam giác BCD. Đẳng thức nào sau đây sai?
A. \(\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} \);
B. \(\overrightarrow {GB} + \overrightarrow {GC} + \overrightarrow {GD} = \overrightarrow 0 \);
C. \(\overrightarrow {OA} + \overrightarrow {OC} = \overrightarrow 0 \);
D. \(\overrightarrow {GC} + \overrightarrow {GO} = \overrightarrow 0 \).
Câu 8:
Tính tổng \(\overrightarrow {MN} + \overrightarrow {PQ} + \overrightarrow {RN} + \overrightarrow {NP} + \overrightarrow {QR} \)
A. \(\overrightarrow {PR} \);
B. \(\overrightarrow {MR} \);
C. \(\overrightarrow {MP} \);
D. \(\overrightarrow {MN} \).
Câu 9:
Cho hình bình hành ABCD. Hãy tìm điểm M để \(\overrightarrow {DM} = \overrightarrow {CB} + \overrightarrow {CD} \).
A. M là một điểm bất kì;
B. M là điểm thỏa mãn ACMD là hình bình hành;
C. M là điểm thỏa mãn ACDM là hình bình hành;
D. Không tồn tại điểm M.
Câu 10:
Cho hình bình hành ABCD tâm O. Ba điểm M, N, P thỏa mãn:
+) \[\overrightarrow {MA} + \overrightarrow {MD} + \overrightarrow {MB} = \overrightarrow 0 \];
+) \[\overrightarrow {N{\rm{D}}} + \overrightarrow {NB} + \overrightarrow {NC} = \overrightarrow 0 \];
+) \[\overrightarrow {PM} + \overrightarrow {PN} = \overrightarrow 0 \].
Nhận xét nào sau đây đúng về M, N, P.
A. M là trung điểm của đoạn thẳng NP;
B. N là trung điểm của đoạn thẳng MP;
C. P là trung điểm của đoạn thẳng MN;
D. Cả A, B, C đều sai.
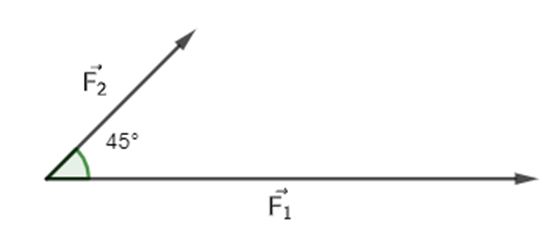
Câu 11:
Hai lực \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) cùng tác động lên một vật, cho \(\left| {\overrightarrow {{F_1}} } \right| = 7N,\left| {\overrightarrow {{F_2}} } \right| = 3N\). Tính độ lớn của hợp lực \(\overrightarrow {{F_1}} + \overrightarrow {{F_2}} \)(biết góc giữa \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) bằng 45°).
A. 10N;
B. 4N;
C. 5,32N;
Câu 12:
Cho lục giác đều ABCDEF và O là tâm. Có bao nhiêu đẳng thức dưới đây là đẳng thức đúng?
1. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OE} = \overrightarrow 0 \);
II. \(\overrightarrow {BC} + \overrightarrow {FE} = \overrightarrow {AD} \);
III. \(\overrightarrow {OA} + \overrightarrow {OB} + \overrightarrow {OE} = \overrightarrow {EB} \);
IV. \(\overrightarrow {AB} + \overrightarrow {CD} + \overrightarrow {FE} = \overrightarrow 0 \).
A. 1;
B. 2;
C. 3;
D. 4.
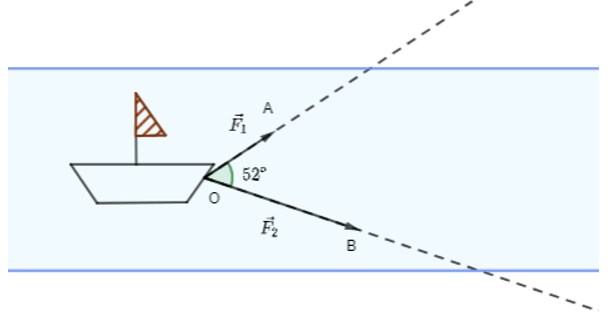
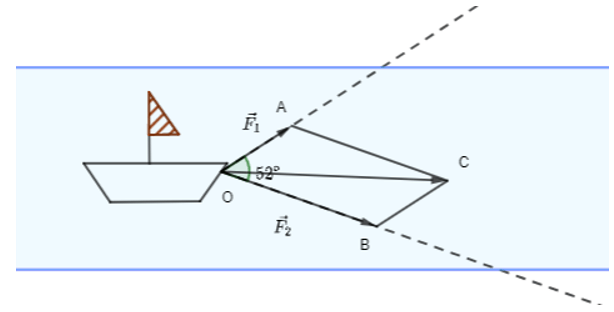
Câu 13:
Hai người cùng kéo một con thuyền với hai lực \[\overrightarrow {{F_1}} = \overrightarrow {OA} ,\,\,\overrightarrow {{F_2}} = \overrightarrow {OB} \] có độ lớn lần lượt là 550 N, 800 N. Cho biết góc giữa hai vectơ là 52o.
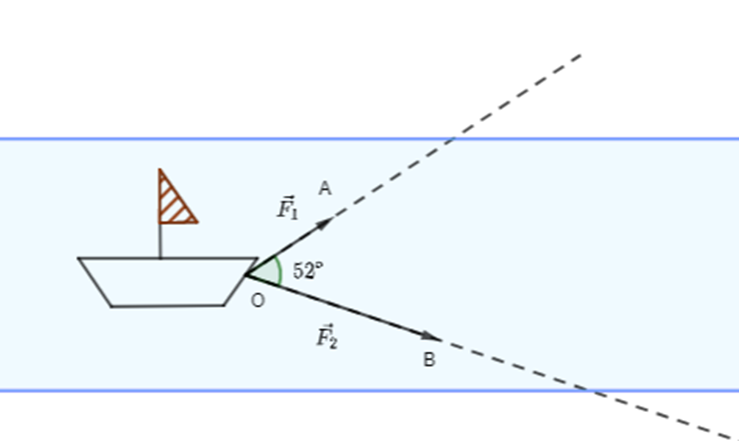
Độ lớn của vectơ hợp lực \[\overrightarrow F \] là tổng của hai lực \[\overrightarrow {{F_1}} \] và \[\overrightarrow {{F_2}} \] nằm trong khoảng nào dưới đây?
A. (900; 1 000);
B. (1 000; 1 100);
C. (1 100; 1 200);
D. (1 200; 1 300).
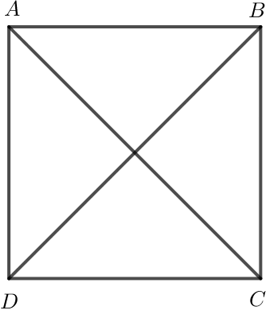
Câu 14:
Cho hình vuông ABCD có cạnh bằng 1. So sánh độ dài của hai vectơ sau:
\[\overrightarrow a = \left( {\overrightarrow {AC} + \overrightarrow {B{\rm{D}}} } \right) + \overrightarrow {CB} \];
\[\overrightarrow b = \overrightarrow {AB} + \overrightarrow {A{\rm{D}}} + \overrightarrow {BC} + \overrightarrow {DA} \].
A. \(\left| {\overrightarrow a } \right| = 2\left| {\overrightarrow b } \right|\);
B. \(\left| {\overrightarrow a } \right| = \left| {\overrightarrow b } \right|\);
C. \(\left| {\overrightarrow a } \right| = \sqrt 2 \left| {\overrightarrow b } \right|\);
D. \(\left| {\overrightarrow a } \right| = \frac{1}{{\sqrt 2 }}\left| {\overrightarrow b } \right|\).
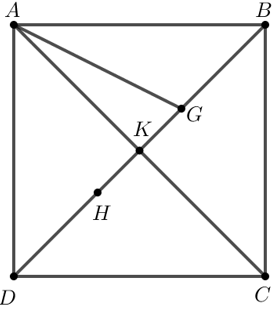
Câu 15:
Cho hình vuông ABCD có cạnh bằng a và ba điểm G, H, K thỏa mãn: \[\overrightarrow {K{\rm{A}}} + \overrightarrow {KC} = \overrightarrow 0 \]; \[\overrightarrow {GA} + \overrightarrow {GB} + \overrightarrow {GC} = \overrightarrow 0 \]; \[\overrightarrow {HA} + \overrightarrow {H{\rm{D}}} + \overrightarrow {HC} = \overrightarrow 0 \]. Tính độ dài các vectơ \[\overrightarrow {GH} \].
A. \[\frac{{\sqrt 2 a}}{2}\];
B. \[\sqrt 2 \]a;
C. \[\frac{{\sqrt 2 a}}{3}\];
D. a