15 Bài tập trắc nghiệm tổng hợp Toán 10 Chương 9 Kết nối tri thức (có đáp án)
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm tổng hợp Toán 10 Chương 9: Tính xác suất theo định nghĩa cổ điển có đáp án và lời giải chi tiết đầy đủ các mức độ sách Kết nối tri thức sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
15 Bài tập trắc nghiệm tổng hợp Toán 10 Chương 9 Kết nối tri thức (có đáp án)
Câu 1. Cho E và là hai biến cố đối nhau. Chọn câu đúng.
A. P(E) = 1 + P();
B. P(E) = P();
C. P(E) = 1 - P();
D. P(E) + P() = 0.
Câu 2. Gieo 3 đồng tiền xu là một phép thử ngẫu nhiên có không gian mẫu là:
A. {NN; NS; SN; SS};
B. {NNN; SSS; NNS; SSN; NSN; SNS};
C. {NNN; SSS; NNS; SSN; NSN; SNS; NSS; SNN};
D. {NNN; SSS; NNS; SSN; NSS; SNN}.
Câu 3. Cho phép thử có không gian mẫu Ω = {1; 2; 3; 4; 5; 6}. Các cặp biến cố không đối nhau là
A. A = {1} và B = {2; 3; 4; 5; 6};
B. C = {1; 4; 5} và D = {2; 3; 6};
C. E = {1; 4; 6} và F = {2; 3};
D. Ω và ∅
Câu 4. Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá át hay lá rô là
A.
B.
C.
D.
Câu 5. Gieo 2 con súc sắc và gọi kết quả xảy ra là tích số hai nút ở mặt trên. Số phần tử của không gian mẫu là:
A. 9;
B. 18;
C. 29;
D. 39.
Câu 6. Gieo con súc sắc hai lần. Gọi A là biến cố để sau hai lần gieo có ít nhất một mặt 6 chấm xuất hiện. Số phần tử của biến cố A là:
A. 8;
B. 9;
C. 10;
D. 11.
Câu 7. Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được một lá rô hay một lá hình người là:
A.
B.
C.
D.
Câu 8. Một bình đựng 5 quả cầu xanh và 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu. Xác suất để được 3 quả cầu khác màu là:
A.
B.
C.
D.
Câu 9. Trong một lớp học gồm có 18 học sinh nam và 17 học sinh nữ. Giáo viên gọi ngẫu nhiên 4 học sinh lên bảng giải bài tập. Xác suất để 4 học sinh được gọi có cả nam và nữ bằng:
A.
B.
C.
D.
Câu 10. Đội thanh niên xung kích của trường THPT có 12 học sinh gồm 5 học sinh khối 12, 4 học sinh khối 11 và 3 học sinh khối 10. Chọn ngẫu nhiên 4 học sinh để làm nhiệm vụ mỗi buổi sáng. Tính xác suất sao cho 4 học sinh được chọn thuộc không quá hai khối.
A.
B.
C.
D.
Câu 11. Trong một hộp có 10 viên bi đánh số từ 1 đến 10, lấy ngẫu nhiên ra hai bi. Tính xác suất để hai bi lấy ra có tích hai số trên chúng là một số lẻ.
A.
B.
C.
D.
Câu 12. Trong giải bóng đá nữ ở trường THPT có 12 đội tham gia, trong đó có hai đội của hai lớp 12A2 và 11A6. Ban tổ chức tiến hành bốc thăm ngẫu nhiên để chia thành hai bảng đấu A, B mỗi bảng 6 đội. Xác suất để 2 đội của hai lớp 12A2 và 11A6 ở cùng một bảng là:
A.
B.
C.
D.
Câu 13. Một con súc sắc cân đối đồng chất được gieo 5 lần. Xác suất để tổng số chấm ở hai lần gieo đầu bằng số chấm ở lần gieo thứ ba:
A.
B.
C.
D.
Câu 14. Cho X = {0; 1; 2; … ; 15}. Chọn ngẫu nhiên 3 số trong tập hợp X. Tính xác suất để trong ba số được chọn không có hai số liên tiếp.
A.
B.
C.
D.
Câu 15. Kết quả (b; c) của việc gieo một con súc sắc cân đối hai lần liên tiếp, trong đó b là số chấm xuất hiện của lần gieo thứ nhất, c là số chấm xuất hiện lần gieo thứ hai được thay vào phương trình bậc hai x2 + bx + c = 0. Tính xác suất để phương trình bậc hai đó vô nghiệm
A.
B.
C.
D.
Câu 1:
Cho E và \(\overline E \) là hai biến cố đối nhau. Chọn câu đúng.
A. P(E) = 1 + P(\(\overline E \));
B. P(E) = P(\(\overline E \));
C. P(E) = 1 - P(\(\overline E \));
D. P(E) + P(\(\overline E \)) = 0.
Câu 2:
Gieo 3 đồng tiền xu là một phép thử ngẫu nhiên có không gian mẫu là:
A. {NN; NS; SN; SS};
B. {NNN; SSS; NNS; SSN; NSN; SNS};
C. {NNN; SSS; NNS; SSN; NSN; SNS; NSS; SNN};
D. {NNN; SSS; NNS; SSN; NSS; SNN}.
Câu 3:
Cho phép thử có không gian mẫu Ω = {1; 2; 3; 4; 5; 6}. Các cặp biến cố không đối nhau là
A. A = {1} và B = {2; 3; 4; 5; 6};
B. C = {1; 4; 5} và D = {2; 3; 6}; .
C. E = {1; 4; 6} và F = {2; 3};
D. Ω và \[\emptyset \].
Câu 4:
Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được lá át hay lá rô là
A. \(\frac{1}{{52}}\);
B. \(\frac{2}{{13}}\);
C. \(\frac{4}{{13}}\);
D. \(\frac{{17}}{{52}}\).
Câu 5:
Gieo 2 con súc sắc và gọi kết quả xảy ra là tích số hai nút ở mặt trên. Số phần tử của không gian mẫu là:
A. 9;
B. 18;
C. 29;
D. 39.
Câu 6:
Gieo con súc sắc hai lần. Gọi A là biến cố để sau hai lần gieo có ít nhất một mặt 6 chấm xuất hiện. Số phần tử của biến cố A là:
A. 8;
B. 9;
C. 10;
D. 11.
Câu 7:
Rút ra một lá bài từ bộ bài 52 lá. Xác suất để được một lá rô hay một lá hình người là:
A. \(\frac{{17}}{{52}}\);
B. \(\frac{{11}}{{26}}\);
C. \(\frac{3}{{13}}\);
D. \(\frac{5}{{13}}\).
Câu 8:
Một bình đựng 5 quả cầu xanh và 4 quả cầu đỏ và 3 quả cầu vàng. Chọn ngẫu nhiên 3 quả cầu. Xác suất để được 3 quả cầu khác màu là:
A. \(\frac{3}{5}\);
B. \(\frac{3}{7}\);
C. \(\frac{3}{{11}}\);
D. \(\frac{3}{{14}}\).
Câu 9:
Trong một lớp học gồm có 18 học sinh nam và 17 học sinh nữ. Giáo viên gọi ngẫu nhiên 4 học sinh lên bảng giải bài tập. Xác suất để 4 học sinh được gọi có cả nam và nữ bằng:
A. \(\frac{{65}}{{71}}\);
B. \(\frac{{69}}{{77}}\);
C. \(\frac{{443}}{{506}}\);
D. \(\frac{{68}}{{75}}\).
Câu 10:
Đội thanh niên xung kích của trường THPT có 12 học sinh gồm 5 học sinh khối 12, 4 học sinh khối 11 và 3 học sinh khối 10. Chọn ngẫu nhiên 4 học sinh để làm nhiệm vụ mỗi buổi sáng. Tính xác suất sao cho 4 học sinh được chọn thuộc không quá hai khối.
Hướng dẫn giải
A. \(\frac{5}{{11}}\);
B. \(\frac{6}{{11}}\);
C. \(\frac{{21}}{{22}}\);
D. \(\frac{{15}}{{22}}\).
Câu 11:
Trong một hộp có 10 viên bi đánh số từ 1 đến 10, lấy ngẫu nhiên ra hai bi. Tính xác suất để hai bi lấy ra có tích hai số trên chúng là một số lẻ.
A. \(\frac{1}{2}\);
B. \(\frac{4}{9}\);
C. \(\frac{1}{9}\);
D. \(\frac{2}{9}\).
Câu 12:
Trong giải bóng đá nữ ở trường THPT có 12 đội tham gia, trong đó có hai đội của hai lớp 12A2 và 11A6. Ban tổ chức tiến hành bốc thăm ngẫu nhiên để chia thành hai bảng đấu A, B mỗi bảng 6 đội. Xác suất để 2 đội của hai lớp 12A2 và 11A6 ở cùng một bảng là:
A. \(\frac{4}{{11}}\);
B. \(\frac{3}{{22}}\);
C. \(\frac{5}{{11}}\);
D. \(\frac{5}{{22}}\).
Câu 13:
Một con súc sắc cân đối đồng chất được gieo 5 lần. Xác suất để tổng số chấm ở hai lần gieo đầu bằng số chấm ở lần gieo thứ ba:
A. \(\frac{{10}}{{216}}\);
B. \(\frac{{15}}{{72}}\);
C. \(\frac{{16}}{{216}}\);
D. \(\frac{5}{{72}}\).
Câu 14:
Cho X = {0; 1; 2; … ; 15}. Chọn ngẫu nhiên 3 số trong tập hợp X. Tính xác suất để trong ba số được chọn không có hai số liên tiếp.
Hướng dẫn giải
A. \(\frac{{13}}{{35}}\);
B. \(\frac{7}{{20}}\);
C. \(\frac{{20}}{{35}}\);
D. \(\frac{{13}}{{20}}\).
Câu 15:
Kết quả (b; c) của việc gieo một con súc sắc cân đối hai lần liên tiếp, trong đó b là số chấm xuất hiện của lần gieo thứ nhất, c là số chấm xuất hiện lần gieo thứ hai được thay vào phương trình bậc hai x2 + bx + c = 0. Tính xác suất để phương trình bậc hai đó vô nghiệm
A. \(\frac{7}{{12}}\);
B. \(\frac{{23}}{{36}}\);
C. \(\frac{{17}}{{36}}\);
D. \(\frac{5}{{36}}\).
Câu 1:
Gieo một xúc xắc 2 lần . Biến cố A là biến cố để sau hai lần gieo có ít nhất 1 mặt 6 chấm
A. A = {(1; 6), (2; 6), (3; 6), (4; 6), (5; 6)};
B. A = {(1; 6), (2; 6), (3; 6), (4; 6), (5; 6), (6; 6)};
C. A = {(1; 6), (2; 6), (3; 6), (4; 6), (5; 6), (6; 6), (6; 1), (6; 2), (6; 3), (6; 4), (6; 5)};
Câu 2:
Chọn ngẫu nhiên một số nguyên dương không lớn hơn 15. Hãy mô ta không gian mẫu trên?
A. Ω = {1; 2; 3; 4; 5; 6; 7; 10; 11; 12; 13; 14; 15};
B. Ω = {1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14};
C. Ω = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14};
Câu 3:
Viết tập hợp Ω là không gian mẫu trong trò chơi tung đồng xu hai lần liên tiếp.
A. Ω = {SS; SN; NS; NN};
B. Ω = {SS; SN; NS };
C. Ω = {SS; NS; NN};
Câu 4:
Một lớp có 20 học sinh nam và 18 học sinh nữ. Chọn ngẫu nhiên một học sinh. Xác suất chọn được 1 học sinh nữ là:
A.
B.
C.
D.
Câu 5:
Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên:
A. Gieo đồng xu để xem xuất hiện mặt ngửa hay mặt sấp;
B. Gieo đồng xu để xem xuất hiện mặt ngửa xuất hiện bao nhiêu lần;
C. Chọn 1 học sinh bất kì trong lớp và xem kết quả là nam hay nữ;
Câu 6:
Sắp xếp năm bạn học sinh An; Bình; Chi; Lệ; Dũng vào một chiếc ghế dài có 5 chỗ ngồi. Xác suất để bạn Chi luôn ngồi chính giữa trong năm bạn là:
A.
B.
C.
D.
Câu 7:
Gieo một đồng tiền cân đối ba lần. Các kết quả có thể xảy ra được biểu diễn trong sơ đồ sau:
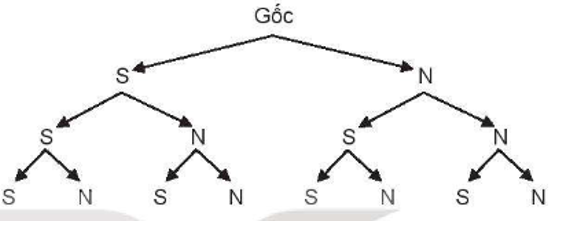
Không gian mẫu là tập:
A. {S; N; S; N; S; N; S; N};
B. {SS; SN; NS; NN};
C. {SSS; SSN; SNS; SNN; NSS; NSN; NNS; NNN};
Câu 8:
Từ các chữ số 1; 2; 4; 6; 8; 9 lấy ngẫu nhiễn một số. Xác suất để lấy được một số nguyên tố là:
A.
B.
C.
D.
Câu 9:
Xác định số phần tử của không gian mẫu các kết quả có thể xảy ra đối với mặt xuất hiện của một xúc xắc sau 3 lần gieo
A. 36;
B. 216;
C. 18;
Câu 10:
Một kệ sách có 3 quyển sách tham khảo Toán, 2 quyển sách tham khảo Văn và 4 quyển sách tham khảo Tiếng Anh. Bạn Hoa lấy ngẫu nhiên 2 quyển sách để học trong ngày hôm nay. Gọi A là biến cố: “Trong 2 quyển sách có 1 quyển sách Toán và 1 quyển sách Tiếng Anh”. Biến P(A) = . Biến cố là gì và có xác suất bằng bao nhiêu?
A. : “Trong 2 quyển sách được chọn không có sách Toán hoặc Tiếng Anh” và P() = ;
B. : “Trong 2 quyển sách được chọn không có sách Toán và Tiếng Anh” và P() = ;
C. : “Trong 2 quyển sách được chọn không có sách Toán” và P() = ;
Câu 1:
Trên giá sách có 4 quyển sách toán, 3 quyển sách lí, 2 quyển sách hoá. Lấy ngẫu nhiên 3 quyển sách. Tính xác suất để 3 quyển lấy ra có ít nhất 2 quyển sách toán. Xác suất để 3 quyển lấy ra có ít nhất 2 quyển môn toán là:
A.
B.
C.
D.
Câu 2:
Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Tính số phần tử của biến cố A :” 4 viên bi lấy ra có ít nhất một viên bi màu đỏ”
A. n(A) = 7366;
B. n(A) = 7563;
C. n(A) = 7566;
Câu 3:
Từ 5 bông hồng vàng, 3 bông hồng trắng, 4 bông hồng đỏ (các bông hồng xem như khác nhau). Người ta muốn chọn ra một bó gồm 7 bông. Gọi A là biến cố “có ít nhất 3 bông hồng vàng và ít nhất 3 bông hồng đỏ” . Số phần tử của biến cố A là:
A. 120;
B. 130;
C. 140;
Câu 4:
Có 3 bó hoa. Bó thứ nhất có 8 hoa hồng, bó thứ hai có 7 bông hoa ly, bó thứ 3 có 6 bông hoa huệ. Chọn ngẫu nhiên 7 hoa từ ba bó hoa trên để cắm vào lọ hoa. Tính xác suất để trong 7 hoa được chọn có số hoa hồng bằng hoa ly.
A.
B.
C.
D.
Câu 5:
Xếp ngẫu nhiên 3 bạn An; Bình ; Cường đứng thành 1 hàng dọc. Tính xác suất để Bình và Cường đứng cạnh nhau.
A.
B.
C.
D.
Câu 6:
Gieo đồng tiền hai lần. Xác xuất để sau hai lần gieo thì kết quả của 2 lần tung là khác nhau:
A.
B.
C.
D.
Câu 7:
Một ban đại diện gồm 5 người được thành lập từ 10 người có tên sau đây: Liên; Mai; Mộc; Thu; Miên; An; Hà; Thanh; Mơ; Kim. Xác suất để đúng 2 người trong ban đại diện có tên bắt đầu bằng chữ M là:
A.
B.
C.
D.
Câu 8:
Một nhóm gồm 8 nam và 7 nữ. Chọn ngẫu nhiên 5 bạn để chơi trò chơi. Xác suất để 5 bạn được chọn có cả nam lẫn nữ mà nam nhiều hơn nữ là:
A.
B.
C.
D.
Câu 9:
Gọi G là biến cố tổng số chấm bằng 7 khi gieo hai con xúc xắc. Số phần tử của G là:
A. 4;
B. 5;
C. 6;
Câu 10:
Một trường THPT có 10 lớp 12, mỗi lớp cử 3 bạn học sinh tham gia thi vẽ tranh cổ động. Các lớp tiến hành bắt tay giao lưu với nhau (các học sinh cùng lớp không bắt tay với nhau). Tính số phần tử của không gian mẫu, biết rằng hai học sinh khác nhau ở hai lớp khác nhau chỉ bắt tay đúng 1 lần.
A. 405;
B. 435;
C. 30;
Câu 11:
Gieo ngẫu nhiên hai con xúc xắc cân đối và đồng chất. Xác suất để sau hai lần gieo được số chấm giống nhau.
A.
B.
C.
D. 1
Câu 12:
Gieo một con xúc xắc. Xác suất để số chấm xuất hiện là số chẵn là:
A. 0,2;
B. 0,3;
C. 0,4;
Câu 13:
Một hộp có 5 viên bi đỏ và 9 viên bi xanh. Chọn ngẫu nhiên 2 viên bi. Xác suất để chọn được hai viên bi khác màu là:
A.
B.
C.
D.
Câu 14:
Gieo một đồng xu cân đối 3 lần liên tiếp. Gọi H là biến cố có hai lần xuất hiện mặt sấp và một lần xuất hiện mặt ngửa. Xác suất biến cố H là:
A.
B.
C.
D.
Câu 15:
Gieo hai con xúc xắc. Xác suất để tổng số chấm trên hai mặt xúc xắc chia hết cho 3 là.
A.
B.
C.
D.
Câu 1:
Một Chi Đoàn có 3 Đoàn viên nữ và một số Đoàn viên nam. Cần lập một đội thanh niên tình nguyện (TNTN) gồm 4 người. Gọi A là biến cố :” 4 người được chọn có 3 nữ” và B là biến cố :” 4 người được chọn toàn nam” . Biết rằng P(A) = P(B). Hỏi Chi Đoàn có bao nhiêu Đoàn viên?
A. 9;
B. 10;
C. 11;
D. 12.
Câu 2:
Lớp 10A có 3 nam, 4 nữ là học sinh tiêu biểu; lớp 10B có 2 nam, 2 nữ là học sinh tiêu biểu. Chọn ngẫu nhiên mỗi lớp 1 bạn để phỏng vấn. Xác suất xảy ra biến cố “trong 2 bạn được chọn có ít nhất 1 nam” gần với giá trị nào nhất sau đây:
A. 0,4;
B. 0,5;
C. 0,2;
Câu 3:
Gọi S là tập hợp tất cả các số tự nhiên có 3 chữ số phân biệt. Chọn ngẫu nhiên một số từ tập S. Xác suất chọn được số lớn hơn 250 là:
A.
B.
C.
D.
Câu 4:
Xếp 3 viên bi xanh (X) và 4 viên bi trắng (T) có kích thước khác nhau thành một hàng ngang, có bao nhiêu kết quả thuận lợi cho biến cố “không có hai bi trắng nào nằm cạnh nhau”?.
A. 6;
B. 30;
C. 24;
Câu 5:
Cho tập hợp A = {2; 3; 4; 5; 6; 7; 8}. Gọi S là tập hợp các số tự nhiên có 4 chữ số đôi một khác nhau được lập thành từ cách chữ số của tập A. Chọn ngẫu nhiên một số từ S, xác suất để số được chọn mà trong mỗi số luôn có mặt hai chữ số chẵn và hai chữ số lẻ là:
A.
B.
C.
D.
