10 Bài tập trắc nghiệm Chương 1 - Cánh diều Toán 9
Haylamdo biên soạn và sưu tầm với 10 bài tập trắc nghiệm tổng hợp Toán 9 Chương 1 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh lớp 9 ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 9.
10 Bài tập trắc nghiệm Chương 1 - Cánh diều Toán 9
I. Nhận biết
Câu 1. Điều kiện xác định của phương trình 1 x − 2 3 = 5 x 2 x − 4
A. x ≠ 0 x ≠ − 4.
B. x ≠ 4.
C. x ≠ 0.
D. x ≠ 0 x ≠ 4.
Hiển thị đáp án
Đáp án: D
Điều kiện xác định của phương trình 1 x − 2 3 = 5 x 2 x − 4 x ≠ 0 x − 4 ≠ 0.
Tức là, x ≠ 0 x ≠ 4.
Vậy ta chọn phương án D.
Câu 2. Hệ số a, b và c tương ứng của phương trình bậc nhất hai ẩn − 7 x − 12 = 0
A. a = − 7 , b = 0 , c = 12.
B. a = − 7 , b = − 12 , c = 0.
C. a = 0 , b = − 7 , c = 12.
D. a = 0 , b = − 12 , c = 0.
Hiển thị đáp án
Đáp án: A
Phương trình bậc nhất hai ẩn x, y là hệ thức dạng a x + b y = c a ≠ 0 b ≠ 0.
Ta viết phương trình − 7 x − 12 = 0 − 7 x + 0 y = 12
Do đó, ta có a = − 7 , b = 0 , c = 12.
Vậy ta chọn phương án A.
Câu 3. Cặp số nào sau đây là nghiệm của phương trình 3 x − 2 y + 1 = 0 ?
A. − 1 ; 1 .
B. 5 ; 3 .
C. 0 ; 1 .
D. − 1 ; − 1 .
Hiển thị đáp án
Đáp án: D
⦁ Thay x = − 1 , y = 1
3 ⋅ − 1 − 2 ⋅ 1 + 1 = − 4 ≠ 0.
Do đó cặp số (-1; 1) không là nghiệm của phương trình 3 x − 2 y + 1 = 0.
⦁ Thay x = 5 , y = 3
3 ⋅ 5 − 2 ⋅ 3 + 1 = 10 ≠ 0.
Do đó cặp số 5 ; 3
⦁ Thay x = 0, y = 1vào phương trình 3x - 2y + 1 = 0,ta được:
3 ⋅ 0 − 2 ⋅ 1 + 1 = − 1 ≠ 0.
Do đó cặp số (0;1) không là nghiệm của phương trình 3x - 2y + 1 = 0
⦁ Thay x = -1, y = -1 vào phương trình 3x - 2y + 1 = 0, ta được:
3.(-1) - 2.(-1) + 1 = 0 (đúng).
Do đó cặp số (-1; -1) là nghiệm của phương trình 3x - 2y + 1 = 0
Vậy ta chọn phương án D.
Câu 4. Cho hệ phương trình 2 x + 9 y = 10 5 y − 3 x = − 6 , a ' , b ' , c '
A. a = 9 , b = 10 , c = 2 a ' = 5 , b ' = − 3 , c ' = − 6.
B. a = 2 , b = 9 , c = 10 a ' = − 3 , b ' = 5 , c ' = − 6.
C. a = 9 , b = 2 , c = − 10 a ' = 5 , b ' = 3 , c ' = − 6.
D. a = 2 , b = 9 , c = 10 a ' = − 3 , b ' = − 5 , c ' = 6.
Hiển thị đáp án
Đáp án: B
Ta viết hệ phương trình 2 x + 9 y = 10 5 y − 3 x = − 6 , 2 x + 9 y = 10 − 3 x + 5 y = − 6 a x + b y = c a ' x + b ' y = c ' .
Trong đó, a = 2 , b = 9 , c = 10 a ' = − 3 , b ' = 5 , c ' = − 6.
Vậy ta chọn phương án B.
Câu 5. Cặp số (1;-5) là nghiệm của hệ phương trình nào trong các hệ phương trình sau đây?
A. x − 5 y = 13 x − y = 3.
B. x − 5 y = 13 2 x − 3 y = − 1.
C. x − y = 6 2 x + y = − 3.
D. x + y = 8 x − y = 3.
Hiển thị đáp án
Đáp án: C
⦁ Thay x = 1, y = -5 vào phương trình x - 5y = 13 ta được: 1 − 5 ⋅ − 5 = 26 ≠ 13.
Do đó cặp số (1;-5) không là nghiệm của hệ phương trình ở các phương án A, B.
⦁ Thay x = 1, y = -5 vào mỗi phương trình trong hệ ở phương án C, ta được:
1 - (-5) = 6 (đúng);
2.1 + (-5) = -3 (đúng).
Do đó cặp số (1;-5) là nghiệm của từng phương trình trong hệ phương trình ở phương án C.
Vì vậy cặp số (1;-5) là nghiệm của hệ phương trình ở phương án C.
⦁ Thay x = 1, y = -5 vào phương trình x + y = 8 ta được: 1 + − 5 = − 4 ≠ 8
Do đó cặp số (1;-5) không là nghiệm của hệ phương trình ở phương án D.
Vậy ta chọn phương án C.
II. Thông hiểu
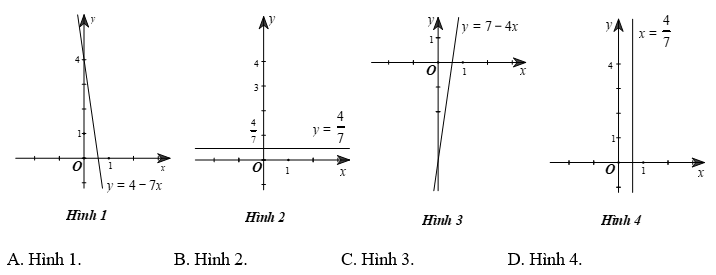
Câu 6. Mỗi nghiệm của phương trình 7 x + 0 y = 4
Hiển thị đáp án
Đáp án: D
Ta có: 7 x + 0 y = 4 x = 4 7 .
Mỗi nghiệm của phương trình 7 x + 0 y = 4 x = 4 7 Hình 4).
Vậy ta chọn phương án D.
Câu 7. Điểm (1;3) không thuộc đường thẳng nào sau đây?
A. 3 x + y = − 4.
B. 3 x − y = − 1.
C. 3 x − y = 5.
D. 3 x + y = 6.
Hiển thị đáp án
Đáp án: D
Với x = 1; y = 3 ta có: 3 x + y = 3 ⋅ 1 + 3 = 6.
Suy ra M 1 ; 3 3 x + y = 6.
Vậy ta chọn phương án D.
Câu 8. Với giá trị nào của x 0 x 0 ; − 2 x − 7 y = 21 ?
A. x 0 = 7.
B. x 0 = − 1.
C. x 0 = − 2.
D. x 0 = 2.
Hiển thị đáp án
Đáp án: A
Thay x = x 0 , y = − 2
x 0 − 7 ⋅ − 2 = 21 x 0 = 7.
Vậy ta chọn phương án A.
Câu 9. Phương trình x 2 − 3 x = 2 x − 6
A. x = 3 và x = 2
B. x = -3 và x = -2
C. x = 3
D. x = -2
Hiển thị đáp án
Đáp án: A
Cách 1. ⦁ Thay x = 3 vào phương trình đã cho, ta được:
3 2 − 3 ⋅ 3 = 2 ⋅ 3 − 6 ,
Do đó x = 3 là một nghiệm của phương trình x 2 − 3 x = 2 x − 6.
⦁ Thay x = 2 vào phương trình đã cho, ta được:
2 2 − 3 ⋅ 2 = 2 ⋅ 2 − 6 ,
Do đó x = 2 là một nghiệm của phương trình x 2 − 3 x = 2 x − 6.
⦁ Thay x = -2 vào phương trình đã cho, ta được:
− 2 2 − 3 ⋅ − 2 = 2 ⋅ − 2 − 6 ,
Do đó x = -2 không là nghiệm của phương trình x 2 − 3 x = 2 x − 6.
Vậy ta chọn phương án A.
Cách 2. Giải phương trình:
x 2 − 3 x = 2 x − 6
x x − 3 = 2 x − 3
x x − 3 − 2 x − 3 = 0
x − 3 x − 2 = 0.
x - 3 = 0 hoặc x - 2 = 0
x = 3 hoặc x = 2.
Vậy phương trình đã cho có hai nghiệm là x = 3 và x = 2.
Do đó ta chọn phương án A.
III. Vận dụng
Câu 10. Cho phương trình 1 x + 1 − 2 x 2 − m x 3 + 1 = 4 x 2 − x + 1 .
A. x = -5
B. x = 5
C. x = 2
D. x = -1
Hiển thị đáp án
Đáp án: A
Với x = 0, ta có:
1 0 + 1 − 2 ⋅ 0 2 − m 0 3 + 1 = 4 0 2 − 0 + 1 .
1 - (-m) = 4
1 + m = 4
m = 3.
Với m = 3, ta có phương trình: 1 x + 1 − 2 x 2 − 3 x 3 + 1 = 4 x 2 − x + 1
Điều kiện xác định: x ≠ − 1.
Từ (1), ta có:
1 x + 1 − 2 x 2 − 3 x + 1 x 2 − x + 1 = 4 x 2 − x + 1
x 2 − x + 1 x + 1 x 2 − x + 1 − 2 x 2 − 3 x + 1 x 2 − x + 1 = 4 x + 1 x + 1 x 2 − x + 1
x 2 − x + 1 − 2 x 2 − 3 = 4 x + 1
x 2 − x + 1 − 2 x 2 + 3 = 4 x + 4
− x 2 − 5 x = 0
− x x + 5 = 0
x = 0 hoặc x + 5 = 0
x = 0 hoặc x = -5.
Do đó phương trình (2) có hai nghiệm là x = 0 và x = -5.
Ta thấy, hai nghiệm x = 0 và x = -5 đều thỏa mãn điều kiện của phương trình (1).
Vậy nghiệm còn lại của phương trình đã cho là x = -5.
Do đó ta chọn phương án A.