10 Bài tập trắc nghiệm Chương 4 - Cánh diều Toán 9
Haylamdo biên soạn và sưu tầm với 10 bài tập trắc nghiệm tổng hợp Toán 9 Chương 4 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh lớp 9 ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 9.
10 Bài tập trắc nghiệm Chương 4 - Cánh diều Toán 9
I. Nhận biết
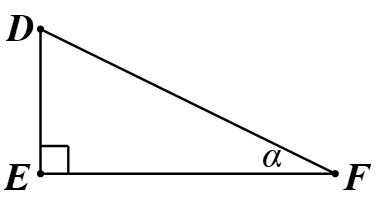
Câu 1. Cho tam giác DEF vuông tại E có góc nhọn F bằng α Khi đó sin α bằng
A. sin α = E F D F
B. sin α = D E D F
C. sin α = D E E F
D. sin α = E F D E
Hiển thị đáp án
Đáp án đúng là: B
Theo định nghĩa tỉ số lượng giác trong tam giác vuông, ta có tam giác DEF vuông tại E nên .Vậy ta chọn phương án B. sin α = D E D F
Câu 2. Cho α tan α = 1 6 c o t α
A. c o t α = 1 6
B. c o t α = - 1 6
C. c o t α = - 6
D. c o t α = 6
Hiển thị đáp án
Đáp án đúng là: D
Theo định nghĩa tỉ số lượng giác trong tam giác vuông, ta có cot α = 1 tan α = 1 : 1 6 = 1 ⋅ 6 = 6.
Vậy ta chọn phương án D.
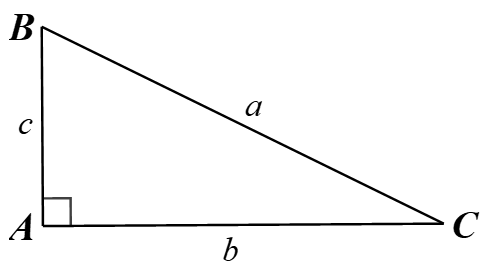
Câu 3. Cho hình vẽ dưới đây.
Hệ thức nào sau đây là đúng?
A. c = a sin B
B. b = a tan C
C. b = c tan B
D. c = a tan B
Hiển thị đáp án
Đáp án đúng là: C
Vì tam giác ABC vuông tại A nên:
⦁ b = a sin B = a cos C = c tan B = c cot C
⦁ c = a sin C = a cos B = c tan B = c cot C
Vậy ta chọn phương án C.
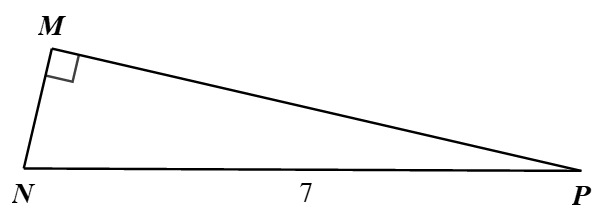
Câu 4. Nếu tam giác MNP vuông tại M có N P = 7 , sin P = 2 9
A. 9 14
B. 18 7
C. 63 2
D. 14 9
Hiển thị đáp án
Đáp án đúng là: D
Vì tam giác MNP vuông tại M nên M N = N P . sin P = 7 . 2 9 = 14 9
Vậy ta chọn phương án D.
Câu 5. Cho α , β
A. sin α - cos α = 0
B. cos α - cos β = 0
C. tan α - c o t β = 0
D. tan α . c o t β = 1
Hiển thị đáp án
Đáp án đúng là: C
Do α , β α + β = 90 ° .
Khi đó sin α = cos β , cos α = sin β , tan α = c o t β , c o t α = tan β tan α . c o t α = 1
Do đó tan α - c o t β = tan α - tan α = 0 .
II. Thông hiểu
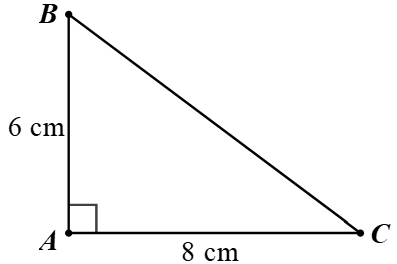
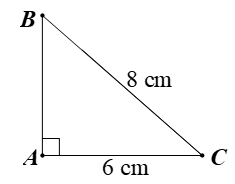
Câu 6. Cho tam giác ABC vuông tại A có A B = 6 c m , A C = 8 c m .
A. sin C = A B B C = 3 5
B. cos C = A C B C = 4 5
C. t a n C = A C A B = 4 3
D. c o t C = A B B C = 3 5
Hiển thị đáp án
Đáp án đúng là: D
Áp dụng định lí Pythagore cho tam giác ABCvuông tại A, ta được: B C 2 = A B 2 + A C 2 = 6 2 + 8 2 = 100 . A B = 10 c m .
Vì tam giác ABC vuông tại A nên:
⦁ sin C = A B B C = 6 10 = 3 5
⦁ cos C = A C B C = 8 10 = 4 5
⦁ t a n C = A C A B = 8 6 = 4 3
⦁ c o t B = A B A C = 6 8 = 3 4 .
Vậy ta chọn phương án D.
Câu 7. Cho góc nhọn α 0 ° < α < 70 °
A = tan α . tan α + 10 ° . tan α + 20 ° . tan 70 ° - α . tan 80 ° - α . tan 90 ° - α
Giá trị của biểu thức là
A. 0.
B. 1.
C. 2.
D. 3.
Hiển thị đáp án
Đáp án đúng là: B
Với 0 ° < α < 70 ° 90 ° - ( 70 ° - α ) = α + 20 ° ; 90 ° - ( 80 ° - α ) = α + 10 ° .
Do đó:
A = tan α . tan α + 10 ° . tan α + 20 ° . tan 70 ° - α . tan 80 ° - α . tan 90 ° - α = tan α . tan α + 10 ° . tan α + 20 ° . c o t ( α + 20 ° ) . c o t ( α + 10 ° ) . c o t α = ( tan α . c o t α ) . tan α + 10 ° . c o t ( α + 10 ° ) . tan α + 20 ° . c o t ( α + 20 ° ) = 1 . 1 . 1 = 1
Câu 8. Cho tam giác ABC vuông tại A có BC = 8cm, AC = 6cm. Kết quả nào sau đây là đúng?
A. tan C = 7 6
B. tan C = 7 6
C. tan C = 7 3
D. tan C = 3 7 7
Hiển thị đáp án
Đáp án đúng là: C
Xét tam giác ABC vuông tại A có: A B 2 + A C 2 = B C 2
Suy ra A B 2 = B C 2 - A C 2 = 8 2 - 6 2 = 28 .
Do đó A B = 2 7
Vì tam giác ABC vuông tại A nên tan C = A B A C = 2 7 6 = 7 3
Do đó ta chọn phương án C.
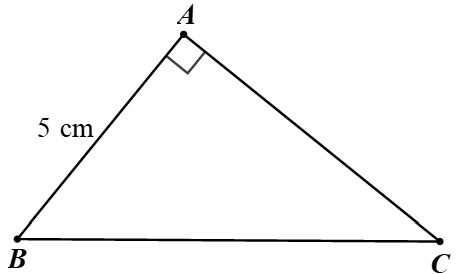
Câu 9. Cho tam giác ABC vuông tại A có A B = 5 cm , cos B = 5 8 .
A. B C = 39 A C = 8
B. B C = 8 A C = 39
C. B C = 16 A C = 39
D. B C = 4 A C = 39 2
Hiển thị đáp án
Đáp án đúng là: B
Xét tam giác ABC vuông tại A, có:
⦁ cos B = A B B C . B C = A B cos B = 5 5 8 = 8
⦁ B C 2 = A B 2 + A C 2
Suy ra A C 2 = B C 2 - A B 2 = 8 2 - 5 2 = 39 . A C = 39
Vậy ta chọn phương án B.
III. Vận dụng
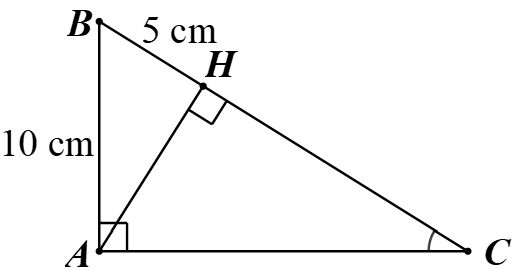
Câu 10. Cho tam giác ABC vuông tại A có AH là đường cao. Biết A B = 10 B H = 5 cos C
A. 2 2
B. 1 2
C. 3 2
D. 3
Hiển thị đáp án
Đáp án đúng là: C
Tam giác ABC vuông tại A có: B ^ + C ^ = 90 ° .
Do đó hai góc B và C phụ nhau nên cos C = sin B .
Tam giác ABC vuông tại A có AH là đường cao nên A H ⊥ B C
Xét tam giác ABH vuông tại H, theo định lí Pythagore, ta có: A B 2 = A H 2 + B H 2
Suy ra A H 2 = A B 2 - B H 2 = 10 2 - 5 2 = 75 . A H = 75 = 5 3
Ta có cos C = sin B = A H A B = 5 3 10 = 3 2 .
Vậy ta chọn phương án C.