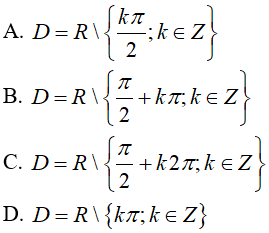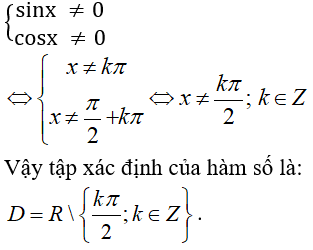Cách tìm tập xác định của hàm số lượng giác cực hay, chi tiết

Cách tìm tập xác định của hàm số lượng giác cực hay, chi tiết

Haylamdo sưu tầm và biên soạn Cách tìm tập xác định của hàm số lượng giác cực hay, chi tiết và lời giải chi tiết đầy đủ các mức độ giúp học sinh ôn tập trắc nghiệm Toán 11 Đại số & Giải tích đạt kết quả cao.

Phương pháp giải

Khi tìm tập xác định của hàm số, ta cần lưu ý:

Các hàm số y = sinx, y = cosx xác định với mọi x ∈R.

- Hàm số y = (P(x))/(Q(x)) xác định khi Q(x) ≠0. Từ đó suy ra:

- Hàm số y = tanx xác định khi cosx ≠0.

- Hàm số y = cotx xác định khi sinx ≠0.

- Hàm số y = √(f(x)) xác định khi f(x) ≥0.

Bài tập minh họa có giải

Ví dụ 1: Tìm tập xác định D của hàm số y = (sinx + 2)/ (sinx.cos2x)

Hướng dẫn giải:

Hàm số xác định khi

Vậy tập xác định của hàm số là D = R\ {kπ/2, k ∈ Z}. Đáp án là A.

Ví dụ 2: Tập xác định D của hàm số y = √((2cosx+3)/(sinx+1)) là:

A. D = R\ {-π/2+kπ, k ∈ Z}

B. D = R\ {-π/2+k2π, k ∈ Z}

C. D = R

D. D = R\ {π/2+k2π, k ∈ Z}

Hướng dẫn giải:

Hàm số xác định khi

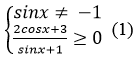
Do – 1 ≤sinx ≤1, – 1 ≤cosx ≤1 nên 2cosx + 3 > 0 và sinx + 1 ≥0, ∀x ∈ R.

Từ đó suy ra (1) ⇔ sinx ≠ -1 ⇔ x ≠ - π/2+k2π.

Vậy tập xác định của hàm số là D = R\ {-π/2+k2π, k ∈ Z}. Đáp án là B.