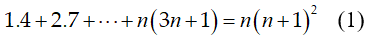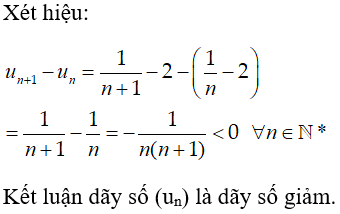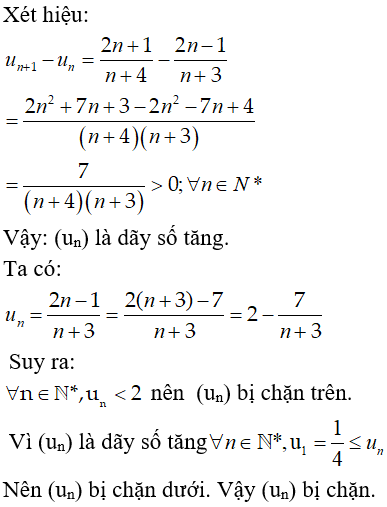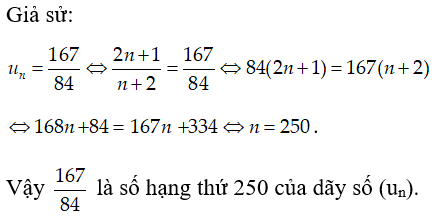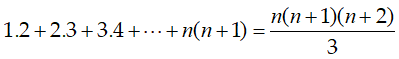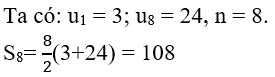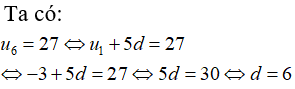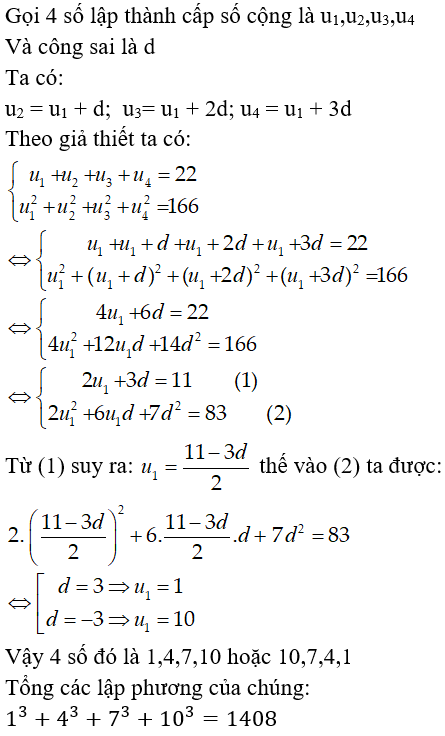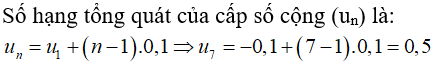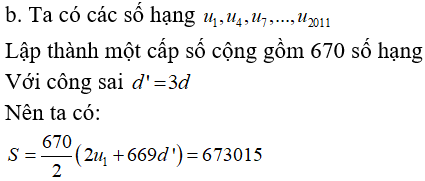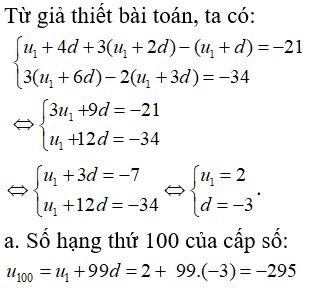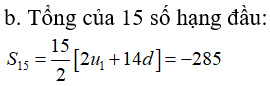100 câu trắc nghiệm Toán 11 Chương 3 (có đáp án): Dãy số - Cấp số cộng và cấp số nhân

---

100 câu trắc nghiệm Toán 11 Chương 3 (có đáp án): Dãy số - Cấp số cộng và cấp số nhân

Haylamdo sưu tầm và biên soạn 100 câu trắc nghiệm Toán 11 Chương 3 (có đáp án): Dãy số - Cấp số cộng và cấp số nhân có đáp án và lời giải chi tiết đầy đủ các mức độ giúp học sinh ôn tập trắc nghiệm Toán 11 Đại số & Giải tích đạt kết quả cao.

• 18 câu trắc nghiệm: Phương pháp quy nạp toán học - Dãy số
• 25 câu trắc nghiệm: Cấp số cộng (phần 1)
• 25 câu trắc nghiệm: Cấp số cộng (phần 2)
• 27 câu trắc nghiệm: Cấp số nhân (phần 1)
• 27 câu trắc nghiệm: Cấp số nhân (phần 2)
• 18 câu trắc nghiệm tổng hợp: Dãy số
• Đề kiểm tra Toán 11 Đại số Chương 3

Trắc nghiệm Phương pháp quy nạp toán học - Dãy số có đáp án

Câu 1: Chứng minh rằng với mọi số nguyên n, ta có:

Hiển thị đáp án

Vậy (1) đúng với n = k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Chọn đáp án

Câu 2: Với mỗi số nguyên dương n, gọi u_n = 9ⁿ - 1. Chứng minh rằng với mọi số nguyên dương n thì u_n luôn chia hết cho 8.

Hiển thị đáp án

* Ta có u₁ = 9¹ - 1 = 8 chia hết cho 8 (đúng với n = 1).

* Giả sử u_k = 9^k - 1 chia hết cho 8.

Ta cần chứng minh u_{k + 1} = 9^{k + 1} - 1 chia hết cho 8.

Thật vậy, ta có:

u_{k + 1} = 9^{k + 1} - 1 = 9.9^k - 1 = 9(9^k - 1) + 8 = 9u_k + 8.

Vì 9u_k và 8 đều chia hết cho 8, nên u_{k + 1} cũng chia hết cho 8.

Vậy với mọi số nguyên dương n thì u_n chia hết cho 8.

Câu 3: Chứng minh rằng với mọi số tự nhiên n ≥ 2, ta luôn có: 2_{n + 1} > 2n + 3 (*)

Hiển thị đáp án

* Với n = 2 ta có 2²⁺¹ > 2.2 + 3 ⇔ 8 > 7 (đúng).

Vậy (*) đúng với n = 2 .

* Giả sử với n = k, k ≥ 2 thì (*) đúng, có nghĩa ta có: 2^{k + 1} > 2k + 3 (1).

* Ta phải chứng minh (*) đúng với n = k + 1, có nghĩa ta phải chứng minh:

2^{k + 2} > 2(k + 1) + 3

Thật vậy, nhân hai vế của (1) với 2 ta được:

2.2^{k + 1} > 2(2k + 3) ⇔ 2^{k + 2} > 4k + 6 > 2k + 5.

(vì 4k + 6 > 4k + 5 > 2k + 5)

Hay 2^{k + 2} > 2(k + 1)+ 3

Vậy (*) đúng với n = k + 1.

Do đó theo nguyên lí quy nạp, (*) đúng với mọi số nguyên dương n ≥ 3 .

Câu 4: Tìm công thức tính số hạng tổng quát u_n theo n của dãy số sau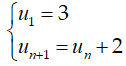

A. u_n = 3n + n² -1

B. u_n = 2n + 1

C. u_n = 4n - 10

D. Đáp án khác

Hiển thị đáp án

Chọn đáp án

Câu 5: Xét tính tăng giảm của dãy số (u_n) biết: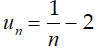

A. Dãy số tăng

B. Dãy số giảm

C. Dãy số không tăng không giảm

D. Dãy số không đổi.

Hiển thị đáp án

Chọn đáp án B

Câu 6: Xét tính tăng hay giảm và bị chặn của dãy số :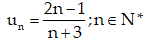

A. Dãy số giảm, bị chặn trên

B. Dãy số tăng, bị chặn dưới

C. Dãy số tăng, bị chặn.

D. Dãy số giảm, bị chặn dưới.

Hiển thị đáp án

Chọn đáp án C

Câu 7: Cho dãy số (u_n) có số hạng tổng quát 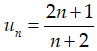. Số 167/84 là số hạng thứ mấy?

A. 300.

B. 212.

C. 250.

D. 249.

Hiển thị đáp án

Chọn đáp án C

Câu 8: Chứng minh bằng quy nạp:

Hiển thị đáp án

Vậy (1) đúng khi n= k + 1. Do đó theo nguyên lí quy nạp, (1) đúng với mọi số nguyên dương n.

Câu 9: Chứng minh bằng phương pháp quy nạp n³ + 11n chia hết cho 6.

Hiển thị đáp án

Câu 10: Tìm công thức tính số hạng tổng quát u_n theo n của dãy số sau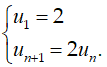

A. u_n = n² - 3n + 10

B. u_n = 2ⁿ

C. u_n = 2n

D. u_n = n + 2

Hiển thị đáp án

Vậy (*) đúng với n = k + 1. Kết luận (*) đúng với mọi số nguyên dương n.

Chọn đáp án B

Trắc nghiệm Cấp số cộng có đáp án

Câu 1: Dãy số (u_n) có phải là cấp số cộng không ? Nếu phải hãy xác định số công sai d, biết rẳng

a. u_n = 2n + 3

A. d = -2

B. d = 3

C. d = 5

D. d = 2

b. u_n = -3n + 1

A. d = -2

B. d = 3

C. d = -3

D. d = 1

c. u_n = n² + 1

A. d = Ø

B. d = 3

C. d = -3

D. d = 1

d. u_n = 2/n

A. d = Ø

B. d = 1/2

C. d = -3

D. d = 1

Hiển thị đáp án

Câu 2: Cho cấp số cộng có 8 số hạng. Số hạng đầu bằng 3 số hạng cuối bằng 24. Tính tổng các số hạng này

A. 105

B. 27

C. 108

D. 111

Hiển thị đáp án

Chọn đáp án C

Câu 3: Cho một cấp số cộng có u₁ = -3; u₆ = 27. Tìm d ?

A. d = 5

B. d = 7

C. d = 6

D. d = 8

Hiển thị đáp án

Chọn đáp án C

Câu 4: Cho 4 số lập thành cấp số cộng. Tổng của chúng bằng 22. Tổng các bình phương của chúng bằng 166. Tổng các lập phương của chúng bằng :

A. 22

B. 166

C. 1752

D. 1408

Hiển thị đáp án

Chọn đáp án D

Câu 5: Cho cấp số cộng (u_n) có: u₁ = -0,1; d = 0,1. Số hạng thứ 7 của cấp số cộng này là:

A. 1,6

B. 6

C. 0,5

D. 0,6

Hiển thị đáp án

Chọn đáp án C

Câu 6: Cho cấp số cộng (u_n) thỏa: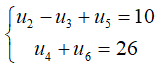

a. Xác định công thức tổng quát của cấp số

A. u_n = 3n - 2

B. u_n = 3n - 4

C. u_n = 3n - 3

D. u_n = 3n - 1

b. Tính S = u₁ + u₄ + u₇ +...+ u₂₀₁₁.

A. S = 673015

B. S = 67334134

C. S = 673044

D. S = 141

Hiển thị đáp án

Chọn đáp án A

Chọn đáp án A

Câu 7: Cho hai cấp số cộng (u_n): 4, 7, 10, 13, 16, ...và (v_n):1, 6, 11, 16, 21, ...Hỏi trong 100 số hạng đầu tiên của mỗi cấp số cộng , có bao nhiêu số hạng chung?

A.10

B. 20

C. 30

D. 40

Hiển thị đáp án

Ứng với 20 giá trị của t cho 20 giá trị của n và 20 giá trị của k.

Vậy có 20 số hạng chung của hai dãy

Chọn đáp án B

Câu 8: Cho cấp số cộng (u_n) thỏa mãn: .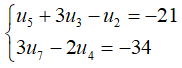

a. Tính số hạng thứ 100 của cấp số ;

A. - 243

B. - 295

C. - 231

D. - 294

b. Tính tổng 15 số hạng đầu của cấp số ;

A. - 244

B. - 274

C. - 253

D. - 285

Hiển thị đáp án

Chọn đáp án B

Chọn đáp án D

Câu 9: Ba số hạng liên tiếp của một cấp số cộng có tổng bằng -9 và tổng các bình phương của chúng bằng 29. Tìm số hạng đầu tiên

A. -3 hoặc – 6

B. – 4 hoặc -2

C. -1 hoặc -5

D. -4 hoặc - 7

Hiển thị đáp án

Chọn đáp án B

Câu 10: Cho tam giác ABC biết 3 góc của tam giác lập thành một cấp số cộng và có góc nhỏ nhất bằng 25°. Tìm 2 góc còn lại?

A. 65° ; 90°.

B. 75° ; 80°.

C. 60° ; 95°.

D. 55°; 100°.

Hiển thị đáp án

Chọn đáp án C