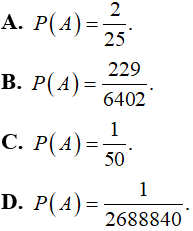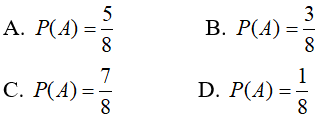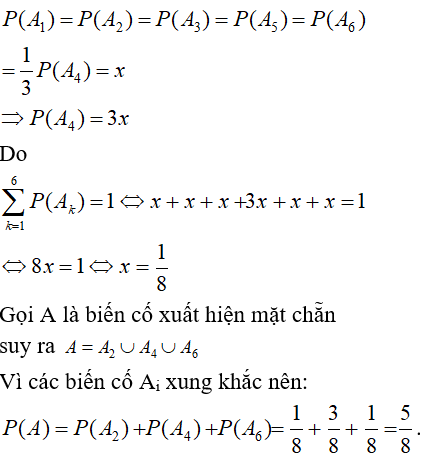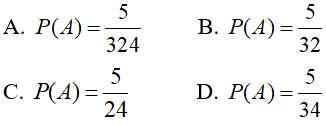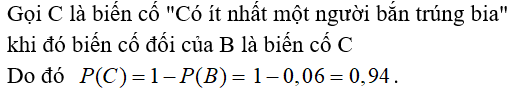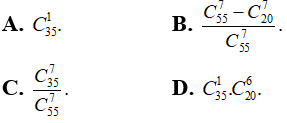Trắc nghiệm Toán 11 Bài 5 (có đáp án): Xác suất của biến cố (phần 1)
Trắc nghiệm Toán 11 Bài 5 (có đáp án): Xác suất của biến cố (phần 1)
Haylamdo sưu tầm và biên soạn Trắc nghiệm Toán 11 Bài 5 (có đáp án): Xác suất của biến cố (phần 1) và lời giải chi tiết đầy đủ các mức độ giúp học sinh ôn tập trắc nghiệm Toán 11 Đại số & Giải tích đạt kết quả cao.
Bài 1: Ba người cùng bắn vào 1 bia. Xác suất để người thứ nhất, thứ hai,thứ ba bắn trúng đích lần lượt là 0,8 ; 0,6; 0,5. Xác suất để có đúng 2 người bắn trúng đích bằng:
A. 0,24.
B. 0,96.
C. 0,46.
D. 0,92.
Chọn đáp án C
Bài 2: Một lô hàng có 100 sản phẩm, biết rằng trong đó có 8 sản phẩm hỏng. Người kiểm định lấy ra ngẫu nhiên từ đó 5 sản phẩm. Tính xác suất của biến cố A: “ Người đó lấy được đúng 2 sản phẩm hỏng” ?
Chọn đáp án B
Bài 3: Một con súc sắc không đồng chất sao cho mặt bốn chấm xuất hiện nhiều gấp 3 lần mặt khác, các mặt còn lại đồng khả năng. Tìm xác suất để xuất hiện một mặt chẵn
Gọi Ai là biến cố xuất hiện mặt i chấm (i = 1, 2, 3, 4, 5, 6)
Do cho mặt bốn chấm xuất hiện nhiều gấp 3 lần mặt khác, nên:
Chọn đáp án A
Bài 4: Gieo một con xúc sắc 4 lần. Tìm xác suất của biến cố
A: “ Mặt 4 chấm xuất hiện ít nhất một lần”
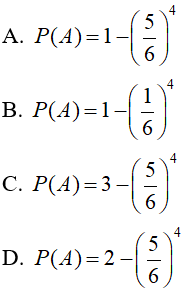
B: “ Mặt 3 chấm xuất hiện đúng một lần”
a. Gọi Ai là biến cố “ mặt 4 chấm xuất hiện lần thứ i” với i = 1; 2; 3; 4.
Khi đó:
Chọn đáp án A
Gọi Bi là biến cố “ mặt 3 chấm xuất hiện lần thứ i” với i = 1; 2; 3; 4
Khi đó:
Chọn đáp án A
Bài 5: Cả hai xạ thủ cùng bắn vào bia. Xác suất người thứ nhất bắn trúng bia là 0,8; người thứ hai bắn trúng bia là 0,7. Hãy tính xác suất để :
1. Cả hai người cùng bắn trúng ;
A. P(A)= 0,75
B. P(A) = 0,6
C. P(A) = 0,56
D. P(A)=0,326
2. Cả hai người cùng không bắn trúng;
A. P(B)=0,04
B.P(B) = 0,06
C. P(B)=0,08
D. P(B) = 0,05
3. Có ít nhất một người bắn trúng.
A. P(C) =0,95
B. P(C) = 0,97
C. P(C) = 0,94
D. P(C) = 0,96
Chọn đáp án C
Chọn đáp án B
Chọn đáp án C
Bài 6: Gieo hai con súc xắc cân đối và đồng chất. Xác suất để tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 7 là:
Số phần tử của không gian mẫu là:
|Ω| = 6.6 = 36.
Gọi biến cố A:
”tổng số chấm trên mặt xuất hiện của hai con súc xắc bằng 7”.
Các kết quả thuận lợi cho A là:
A= {(1; 6); (2; 5); (3; 4); (4; 3); (5; 2); (6; 1)}.
Do đó, |Ω6| = 6 . Vậy P(A) = 6/36 = 1/6 .
Chọn đáp án B
Bài 7: Gieo 3 con súc sắc cân đối và đồng chất. Xác suất để số chấm xuất hiện trên 3 con súc sắc đó bằng nhau:
Số phần tử của không gian mẫu là:
|Ω| = 63 = 216
A: “số chấm xuất hiện trên 3 con súc sắc đó bằng nhau”.
A = {(1,1,1); (2,2,2); (3,3,3); (4,4,4); (5,5,5); (6,6,6)}
⇒ |ΩA| = 6
Xác suất để số chấm xuất hiện trên 3 con súc sắc đó bằng nhau là:
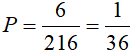
Chọn đáp án D
Bài 8: Có hai hộp đựng bi. Hộp I có 9 viên bi được đánh số 1, 2, 3....., 9. Lấy ngẫu nhiên mỗi hộp một viên bi. Biết rằng xác suất để lấy được viên bi mang số chẵn ở hộp II là 3/10. Xác suất để lấy được cả hai viên bi mang số chẵn là:
Chọn đáp án A
Bài 9: Một hộp chứa 5 viên bi màu trắng, 15 viên bi màu xanh và 35 viên bi màu đỏ. Lấy ngẫu nhiên từ hộp ra 7 viên bi. Xác suất để trong số 7 viên bi được lấy ra có ít nhất 1 viên bi màu đỏ là:
Chọn đáp án B
Bài 10: Một nhóm gồm 8 nam và 7 nữ. Chọn ngẫu nhiên 5 bạn. Xác suất để trong 5 bạn được chọn có cả nam lẫn nữ mà nam nhiều hơn nữ là:
Chọn đáp án B
