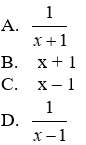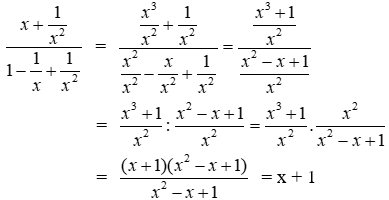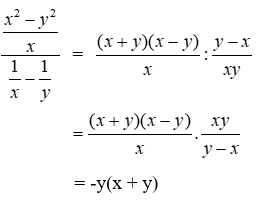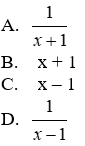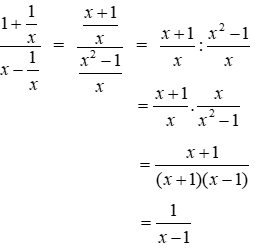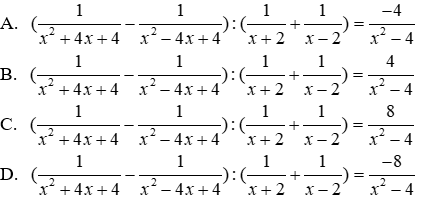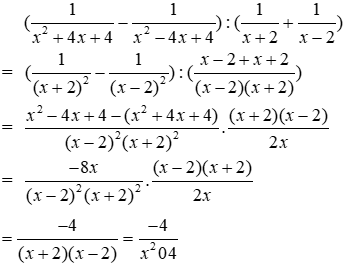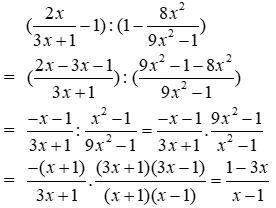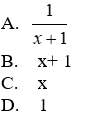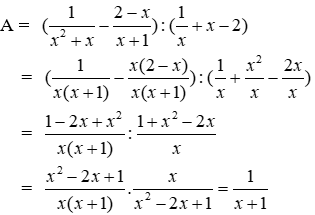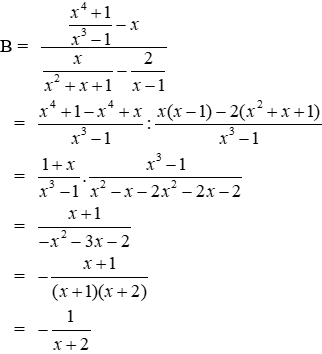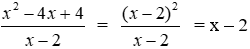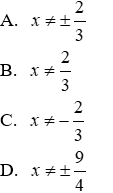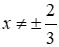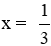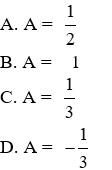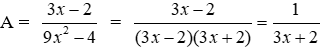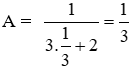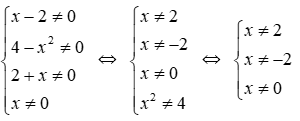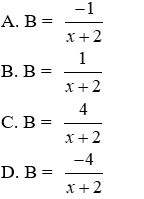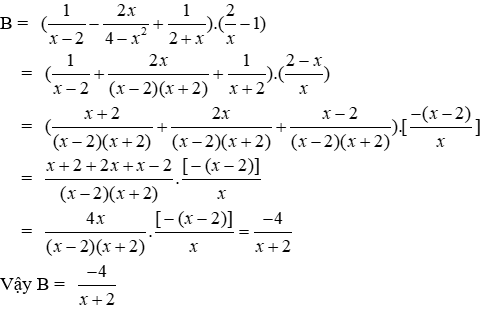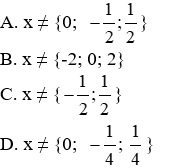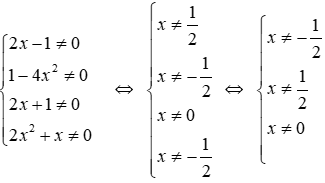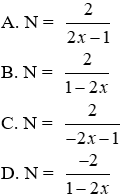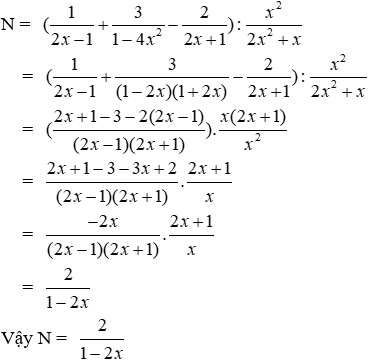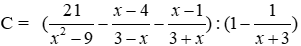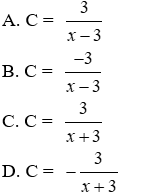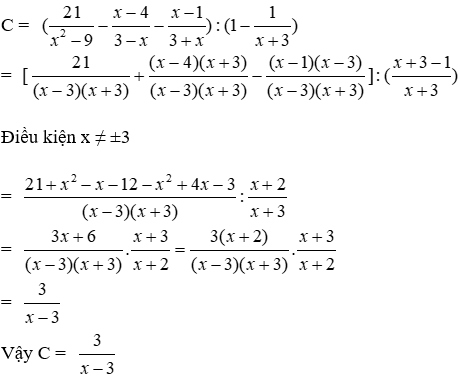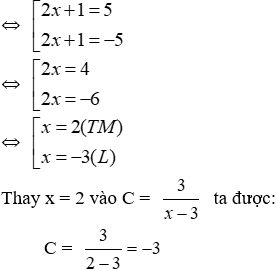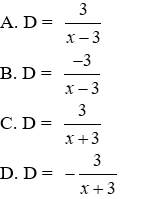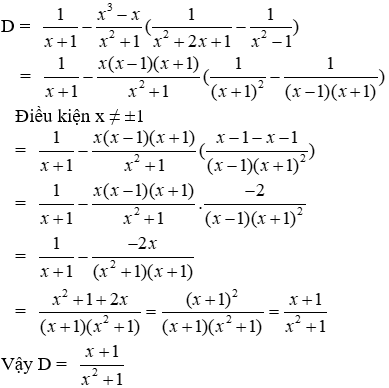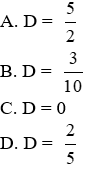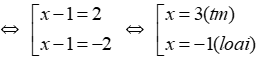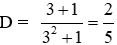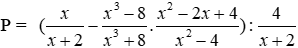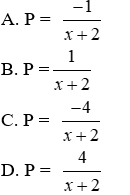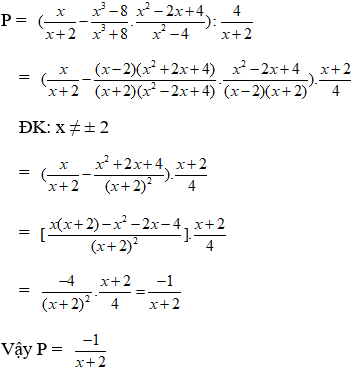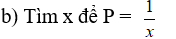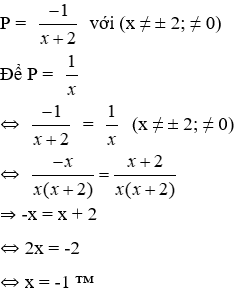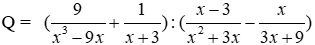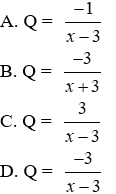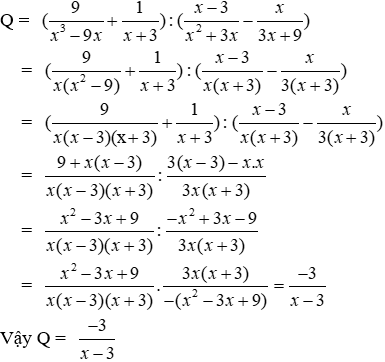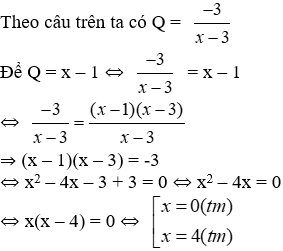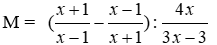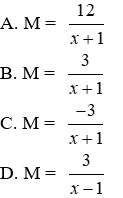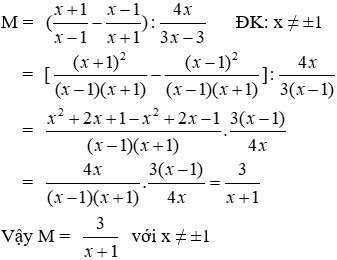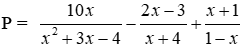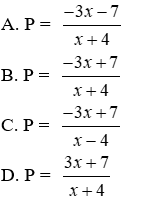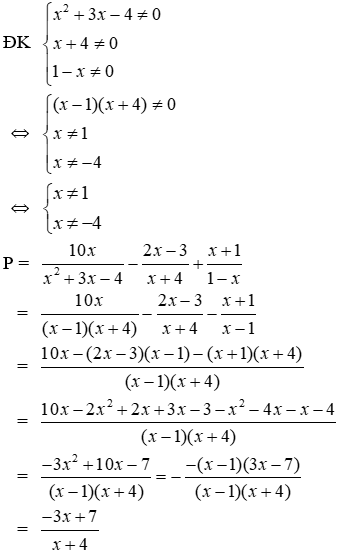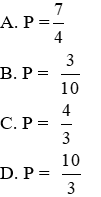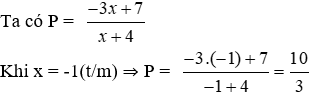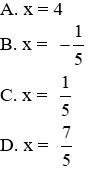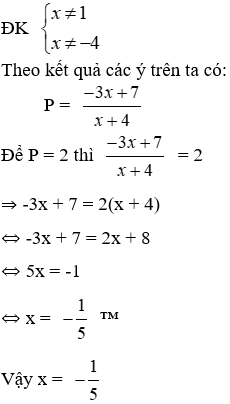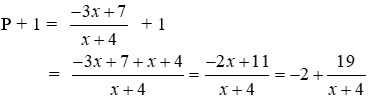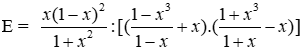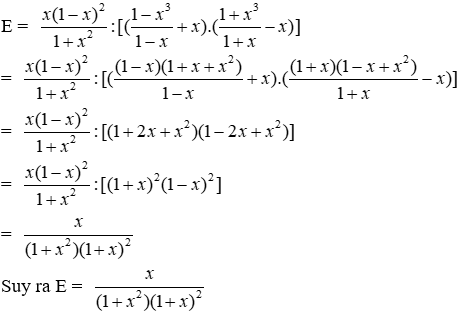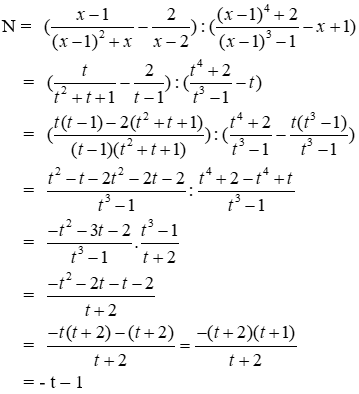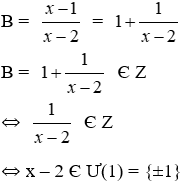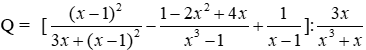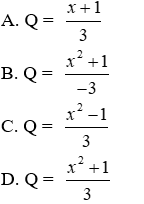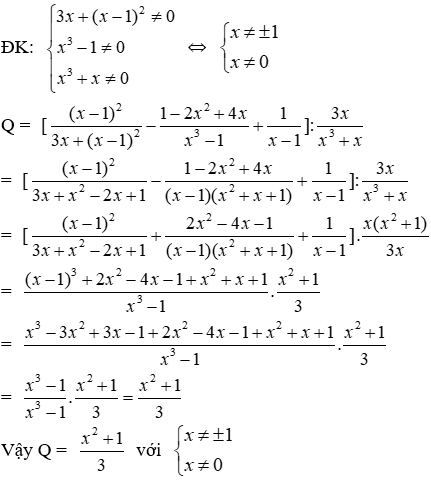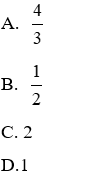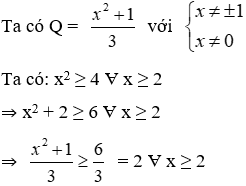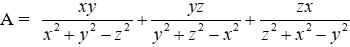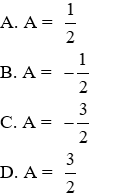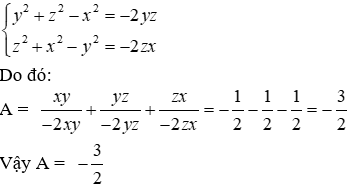Trắc nghiệm Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức có đáp án - Toán lớp 8

---

Trắc nghiệm Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức có đáp án

Với bộ bài tập Trắc nghiệm Biến đổi các biểu thức hữu tỉ. Giá trị của phân thức Toán lớp 8 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 8.

Bài 1: Biểu thức 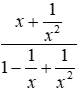 được biến đổi thành phân thức đại số là

Hiển thị đáp án

Lời giải

Ta có:

Đáp án cần chọn là: B

Bài 2: Biến đổi biểu thức hữu tỉ 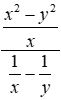 ta được kết quả là:

A. - y(x – y)    

B. y(x – y)      

C. y(x + y)      

D. - y(x + y)

Hiển thị đáp án

Lời giải

ĐKXĐ: x ≠0; y ≠ 0; x ≠ y.

Ta có:

Đáp án cần chọn là: D

Bài 3: Biến đổi biểu thức 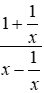 thành biểu thức đại số

Hiển thị đáp án

Lời giải

Ta có:

Đáp án cần chọn là: D

Bài 4: Chọn khẳng định đúng

Hiển thị đáp án

Lời giải

Ta có:

Đáp án cần chọn là: A

Bài 5: Thực hiện phép tính sau 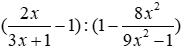, ta được kết quả là:

Hiển thị đáp án

Lời giải

Đáp án cần chọn là: A

Bài 6: Biết A = 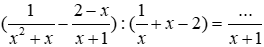. Điền biểu thức thích hợp vào ô trống

Hiển thị đáp án

Lời giải

Ta có:

Vậy số cần điền là 1.

Đáp án cần chọn là: D

Bài 7: Trong trường hợp biểu thức A có nghĩa thì 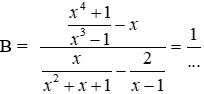. Điều biểu thức thích hợp vào chỗ trống.

A. -x + 2         

B. x – 2          

C. -x – 2         

D. x + 2

Hiển thị đáp án

Lời giải

Ta có:

Vậy ta cần điền là: – x – 2

Đáp án cần chọn là: C

Bài 8: Cho phân thức

a) Tìm điều kiện của x để phân thức xác định

A. x = 2          

B. x ≠ 2          

C. x > 2

D. x < 2

Hiển thị đáp án

Lời giải

Phân thức 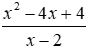 xác định khi x – 2 ≠ 0 ⇔ x ≠ 2

Đáp án cần chọn là: B

b) Tính giá trị biểu thức khi x = 2020

A. 2018          

B. 2022          

C. 2016          

D. 2024

Hiển thị đáp án

Lời giải

Ta có:

Thay x = 2020 (thỏa mãn điều kiện x ≠ 2) vào biểu thức x – 2 ta được 2020 – 2 = 2018.

Vậy với x = 2020 thì giá trị biểu thức là 2018

Đáp án cần chọn là: A

Bài 9: Cho phân thức

a) Tìm điều kiện của x để phân thức xác định

Hiển thị đáp án

Lời giải

Phân thức 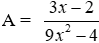 xác định khi 9x² – 4 ≠ 0 ⇔ 9x² ≠ 4 ⇔

Đáp án cần chọn là: A

b) Tính giá trị biểu thức khi

Hiển thị đáp án

Lời giải

Ta có:

  

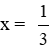
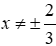
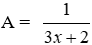
Thay  (thỏa mãn điều kiện ) vào biểu thức  ta được:

  

Vậy với x = 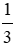 thì giá trị biểu thức là A =

Đáp án cần chọn là: C

Bài 10: Cho biểu thức

a) Với giá trị nào của x thì B xác định

A. x ≠ {0; 2}

B. x ≠ {-2; 0; 2}

C. x ≠ {-2; 2}

D. x ≠ {0; 2}

Hiển thị đáp án

Lời giải

Phân thức 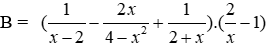 xác định khi

 

Đáp án cần chọn là: B

b) Rút gọn B ta được

Hiển thị đáp án

Lời giải

Đáp án cần chọn là: D

Bài 11: Cho biểu thức

a) Với giá trị nào của x thì N xác định

Hiển thị đáp án

Lời giải

Phân thức 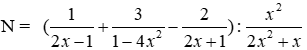 xác định khi

Đáp án cần chọn là: A

b) Rút gọn N ta được

Hiển thị đáp án

Lời giải

Đáp án cần chọn là: B

Bài 12: Cho

a) Rút gọn C ta được

Hiển thị đáp án

Lời giải

Ta có:

Đáp án cần chọn là: A

b) Tính giá trị biểu thức C tại x thỏa mãn |2x + 1| = 5

A. C =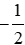      

B. C = 3          

C. C = -3        

D. C = 0

Hiển thị đáp án

Lời giải

Ta có |2x + 1| = 5

Đáp án cần chọn là: C

Bài 12: Cho 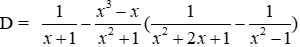 với x ≠ ±1.

a) Rút gọn D ta được

Hiển thị đáp án

Lời giải

Ta có:

Đáp án cần chọn là: B

b) Tính giá trị biểu thức D tại x thỏa mãn |x – 1| = 2.

Hiển thị đáp án

Lời giải

Điều kiện x ≠ ±1

Ta có |x – 1| = 2

Thay x = 3 vào 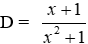 (theo câu trước) ta được

Đáp án cần chọn là: D

Bài 13: Cho

a) Biểu thức rút gọn của P là

Hiển thị đáp án

Lời giải

Ta có:

Đáp án cần chọn là: A

A. x = 2          

B. x = 1          

C. x = -1         

D. x = -2

Hiển thị đáp án

Lời giải

Theo câu trên ta có:

Vậy x = -1

Đáp án cần chọn là: C

Bài 14: Cho

a) Biểu thức rút gọn của Q là

Hiển thị đáp án

Lời giải

ĐK: x ≠ ±3

Đáp án cần chọn là: D

b) Tìm x để Q = x – 1

A. x = 0; x = 4

B. x = 4          

C. x = 0          

D. x = 0; x = -4

Hiển thị đáp án

Lời giải

ĐK: x ≠ ±3

Vậy x = 0; x = 4 thỏa mãn yêu cầu đề bài

Đáp án cần chọn là: A

Bài 15: Cho

a) Rút gọn M ta được

Hiển thị đáp án

Lời giải

Ta có:

Đáp án cần chọn là: B

Hiển thị đáp án

Lời giải

Đáp án cần chọn là: A

Bài 16: Cho

a) Rút gọn P ta được

Hiển thị đáp án

Lời giải

Đáp án cần chọn là: B

b) Tính P khi x = -1

Hiển thị đáp án

Lời giải

Đáp án cần chọn là: D

c) Để P = 2 thì giá trị của x là:

Hiển thị đáp án

Lời giải

Đáp án cần chọn là: B

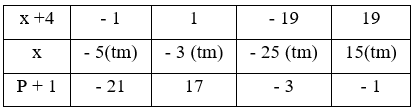
d) Tìm x Є Z để P + 1 Є Z

A. x Є {-25; -5; -3; 15}                     

B. x Є {-25; -5; -3}

C. x Є {5; -5; -3; 15}             

D. x Є {-25; 15}

Hiển thị đáp án

Lời giải

x Є Z để P + 1 Є Z ⇒ (x + 4) Є Ư(19) = {±1; ±19}

Vậy x Є {-25; -5; -3; 15} thì P + 1 Є Z

Đáp án cần chọn là: A

Bài 17: Cho

Chọn câu đúng.

A. E > 0 với mọi x ± 1                       

B. E > 0 với mọi x> 0; x ≠ 1

C. E > 0 với mọi x < 0                       

D. E< 0 với mọi x> 0; x ≠ 1

Hiển thị đáp án

Lời giải

Đk: x ± 1

Ta có:

Ta thấy với x ± 1 thì 1 + x² ≥ 1 > 0 và (1+ x)² > 0 nên (1 + x²)(1 + x)² > 0

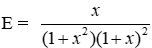
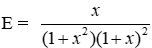
Suy ra  > 0 ⇒ x > 0 nên B đúng, A, C sai

 < 0 ⇒ x < 0 nên D sai

Đáp án cần chọn là: B

Bài 18: Cho 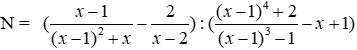 với x là một số nguyên. Chọn câu đúng.

A. Giá trị của N luôn là số nguyên

B. Giá trị của N luôn là số nguyên dương

C. Giá trị của N luôn bằng 0  

D. Giá trị của N luôn không âm

Hiển thị đáp án

Lời giải

ĐK x ≠ 2

Đặt x – 1 = t. ta có x = t +1; x – 2 = t – 1

Dó đó:

Thay x – 1 = t ta được N = -(x – 1) – 1 = -x

Vì x là số nguyên nên giá trị của N cũng luôn là số nguyên

Đáp án cần chọn là: A

Bài 19: Cho 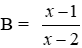. Số giá trị của x Є Z để B Є Z là:

A. 3                

B. 0                

C. 2                

D. -2

Hiển thị đáp án

Lời giải

ĐKXĐ: x ≠ 2

Ta có:

Đáp án cần chọn là: C

Bài 20: Cho

a) Rút gọn Q ta được

Hiển thị đáp án

Lời giải

Đáp án cần chọn là: D

b) Giá trị nhỏ nhất của Q với x ≥ 2 là

Hiển thị đáp án

Lời giải

Dấu "=" xảy ra khi x = 2 (tm).

Vậy Min Q = 2 ⇔ x = 2

Đáp án cần chọn là: C

Bài 21: Cho x; y; z ≠ 0 thỏa mãn x - y + z = 0. Tính giá trị biểu thức:

Hiển thị đáp án

Lời giải

Từ x + y + z = 0 ⇒ x + y = -z ⇒ x² + 2xy + y² = z² ⇒ x² + y² – z² = -2xy

Đáp án cần chọn là: C