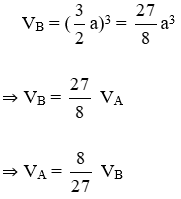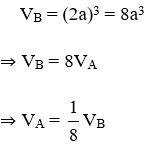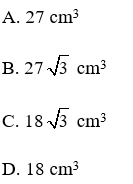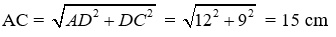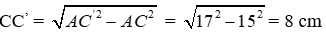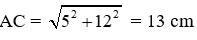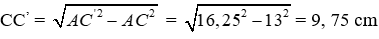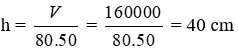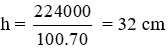Trắc nghiệm Thể tích của hình hộp chữ nhật có đáp án - Toán lớp 8
Trắc nghiệm Thể tích của hình hộp chữ nhật có đáp án
Với bộ bài tập Trắc nghiệm Thể tích của hình hộp chữ nhật Toán lớp 8 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 8.
Bài 1: Hãy chọn câu đúng. Hình hộp chữ nhật có ba kích thước lần lượt là: a, 2a, 
thể tích của hình hộp chữ nhật đó là:
A. a2
B. 4a2
C. 2a2
D. a3
Lời giải
Thê tích của hình hộp chữ nhật là: V = a.2a. = a3 (đvtt)
Đáp án cần chọn là: D
Bài 2: Hãy chọn câu đúng. Hình hộp chữ nhật có ba kích thước lần lượt là: a, a, 2a thể tích của hình hộp chữ nhật đó là:
A. a2
B. 2a3
C. 2a4
D. a3
Lời giải
Thê tích của hình hộp chữ nhật là: V = a.a.2a = 2a3 (đvtt)
Đáp án cần chọn là: B
Bài 3: Hãy chọn câu đúng. Cạnh của một hình lập phương bằng 5 cm khi đó thể tích của nó là:
A. 25 cm3
B. 50 cm3
C. 125 cm3
D. 625 cm3
Lời giải
Thê tích của hình lập phương cạnh 5 cm là: V = 53 = 125 cm3
Đáp án cần chọn là: C
Bài 4: Thể tích của một hình lập phương a (cm) là:
A. a3 (cm3)
B. 2a3 (cm3)
C. 3a3 (cm3)
D. 6a (cm3)
Lời giải
Thê tích của hình lập phương cạnh 5 cm là: V = a3 (cm3)
Đáp án cần chọn là: A
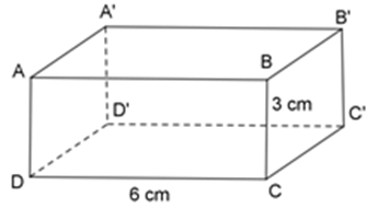
Bài 5: Các kích thước của hình hộp chữ nhật ABCD. A'B'C'D' là DC= 6 cm, CB = 3 cm. Hỏi độ dài của A'B' và AD là bao nhiêu cm
A. 3 cm và 6 cm
B. 6 cm và 9 cm
C. 6 cm và 3 cm
D. 9 cm và 6 cm
Lời giải
Vì ABCD. A'B'C'D' là hình hộp chữ nhật nên ABCD, ABB'A' là hình chữ nhật.
Xét hình chữ nhật ABCD có: AD = BC = 3 cm, DC= AB = 6cm
Xét hình chữ nhật ABB'A' có: A'B' = AB = 6cm
Vậy A'B' và AD lần lượt dài 6 cm và 3 cm.
Đáp án cần chọn là: C
Bài 6: Các kích thước của hình hộp chữ nhật ABCD. A'B'C'D' là CC'= 4 cm, DC = 6 cm, CB = 3 cm. Chọn kết luận không đúng:
A. AD = 3 m
B. D'C' = 4 cm
C. AA' = 4 cm
D. A'B' = 6 cm
Lời giải
Vì ABCD. A'B'C'D' là hình hộp chữ nhật nên ABCD, ABB'A' là hình chữ nhật.
Xét hình chữ nhật ABCD có: AD = BC = 3 cm
Xét hình chữ nhật CDD'C' có: D'C' = DC = 6 cm
Xét hình chữ nhật AA'C'C có: AA' = C'C = 4 cm
Xét hình chữ nhật ABB'A' có: A'B' = AB = 6cm
Vậy AD = 3 cm, D'C' = 6 cm, AA' = 4 cm, A'B' = 6cm
Đáp án cần chọn là: B
Bài 7: Một bể nước dạng hình hộp chữ nhật có kích thước các số đo trong lòng bể là: dài 4 m, rộng 3 m, cao 2, 5 m. Biết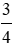 
bể đang chứa nước. Hỏi thể tích phần bể không chứa nước là bao nhiêu?
A. 30 m3
B. 22, 5 m3
C. 7, 5 m3
D. 5, 7 m3
Lời giải
Vì bể nước có dạng hình hộp chữ nhật nên ta tính được thể tích bể nước là:
V = 4.3.2, 5 = 30 m3
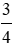
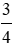
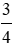
Vì bể đang chứa nước nên thể tích phần bể chứa nước là: Vchứa nước = V = .30 = 22, 5 m3
Vậy thể tích phần bể không chức nước là: Vkhông chứa nước = V - Vchứa nước = 30 – 22, 5 = 7, 5 m3
Đáp án cần chọn là: C
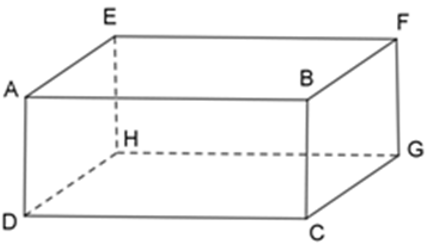
Bài 8: Cho hình hộp chữ nhật ABCD. EFGH. Các đường thẳng nào vuông góc với mặt phẳng (EFGH)?
A. AE, AB, BF, CG
B. AE, BF, AB, DH
C. AE, DH, CG, BF
D. AE, AB, CD, CG
Lời giải
Vì ABCD. EFGH là hình hộp chữ nhật nên ABFE, BCGF, CDHG, DAEH là hình chữ nhật.
Ta có:
+ AE ⊥ EF (vì ABEF là hình chữ nhật)
+ AE ⊥ EH (vì DAEH là hình chữ nhật)
⇒ AE ⊥ mp (EFGH)
Ta có:
+ BF ⊥ EF (vì ABEF là hình chữ nhật)
+ BF ⊥ FG (vì BCGF là hình chữ nhật)
⇒ BF ⊥ mp (EFGH)
Ta có:
+ CG ⊥ GF (vì BCGF là hình chữ nhật)
+ CG ⊥ GH (vì CDHG là hình chữ nhật)
⇒ CG ⊥ mp (EFGH)
Ta có:
+ DH ⊥ HG (vì CDHG là hình chữ nhật)
+ DH ⊥ HE (vì DAEH là hình chữ nhật)
⇒ DH ⊥ mp (EFGH)
Vậy AE, BF, CG, DH đều vuông góc với mặt phẳng (EFGH)
Đáp án cần chọn là: C
Bài 9: Cho hình hộp chữ nhật ABCD. EFGH. Đường thẳng nào dưới đây không vuông góc với mặt phẳng (EFGH)?
A. AE
B. BF
C. CG
D. AB
Lời giải
Vì ABCD. EFGH là hình hộp chữ nhật nên ABFE, BCGF, CDHG, DAEH là hình chữ nhật.
Ta có:
+ AE ⊥ EF (vì ABEF là hình chữ nhật)
+ AE ⊥ EH (vì DAEH là hình chữ nhật)
⇒ AE ⊥ mp (EFGH)
Ta có:
+ BF ⊥ EF (vì ABEF là hình chữ nhật)
+ BF ⊥ FG (vì BCGF là hình chữ nhật)
⇒ BF ⊥ mp (EFGH)
Ta có:
+ CG ⊥ GF (vì BCGF là hình chữ nhật)
+ CG ⊥ GH (vì CDHG là hình chữ nhật)
⇒ CG ⊥ mp (EFGH)
Do đó A, B, C đúng.
Đáp án D sai vì AB // EF và EF nằm trong mp (EFGH) nên AB// (EFGH).
Đáp án cần chọn là: D
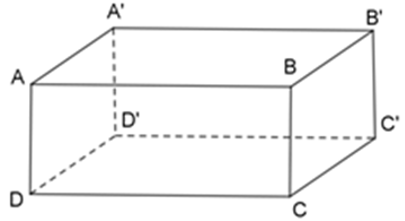
Bài 10: Cho hình hộp chữ nhật ABCD. A'B'C'D'. Đường thẳng BB' vuông góc với các mặt phẳng nào?
A. (ABCD) và (A'B'C'D')
B. (ABCD) và (A'B'BA)
C. (BCC'B') và (A'B'C'D')
D. (ABCD) và (ABC'D')
Lời giải
Ta có: BB' ⊥ BC (Vì BCC'B' là hình chữ nhật), BB' ⊥ BA (Vì ABB'A' là hình chữ nhật) ⇒ BB'⊥ mp (ABCD)
Ta có: BB' ⊥ B'C' (Vì BCC'B' là hình chữ nhật), BB' ⊥ B'A' (Vì ABB'A' là hình chữ nhật) ⇒ BB'⊥ mp (A'B'C'D') ⇒ BB'⊥ mp (A'B'C'D')
Vậy BB' vuông góc với mặt phẳng (ABCD) và mặt phẳng A'B'C'D'
Đáp án cần chọn là: A
Bài 11: Cho hình hộp chữ nhật ABCD. A'B'C'D'. Đường thẳng BB' vuông góc với các mặt phẳng nào?
A. (ABCD)
B. (A'B'BA)
C. (BCC'B')
D. (ABC'D')
Lời giải
Ta có: BB' ⊥ BC (Vì BCC'B' là hình chữ nhật), BB' ⊥ BA (Vì ABB'A' là hình chữ nhật) ⇒ BB'⊥ mp (ABCD)
Đáp án cần chọn là: A
Bài 12: Hình lập phương A có cạnh bằng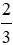 
cạnh hình lập phương B. Hỏi thể tích hình lập phương A bằng bao nhiêu phần thẻ tích hình lập phương B
Lời giải
Gọi chiều dài một cạnh của hình lập phương A là a.
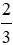
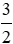
Vì hình lập phương A có cạnh bằng cạnh của hình lập phương B nên chiều dài 1 cạnh của hình lập phương B là 
a
Thể tích hình lập phương A là: VA = a3.
Thể tích hình lập phương B là:
Vậy thể tích hình lập phương A bằng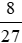 
thể tích hình lập phương B
Đáp án cần chọn là: C
Bài 13: Hình lập phương A có cạnh bằng 
cạnh hình lập phương B. Hỏi thể tích hình lập phương A bằng bao nhiêu phần thể tích hình lập phương B
Lời giải
Gọi chiều dài một cạnh của hình lập phương A là a.
Vì hình lập phương A có cạnh bằng cạnh của hình lập phương B nên chiều dài 1 cạnh của hình lập phương B là 2a
Thể tích hình lập phương A là: VA = a3.
Thể tích hình lập phương B là:
Vậy thể tích hình lập phương A bằng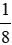 
thể tích hình lập phương B
Đáp án cần chọn là: A
Bài 14: Một chiếc hộp hình lập phương không có nắp được sơn cả mặt trong và mặt ngoài. Diện tích phải sơn tổng cộng là 1440 cm2. Tính thể tích của hình lập phương đó.
A. 1782 cm3
B. 1728 cm3
C. 144 cm3
D. 1827 cm3
Lời giải
Chiếc hộp hình lập phương không nắp gồm 5 hình vuông, mỗi hình vuông được sơn 2 mặt nên diện tích mỗi hình vuông là: 1440 : 10 = 144 (cm2)
Vì diện tích hình vuông bằng hình bình phương một cạnh nên cạnh của hình lập phương bằng 12 cm nên thể tích của hình lập phương bằng 123 = 1728 (cm3)
Đáp án cần chọn là: B
Bài 15: Một chiếc hộp hình lập phương không có nắp được sơn cả mặt trong và mặt ngoài. Diện tích phải sơn tổng cộng là 2880 cm2. Tính thể tích của hình lập phương đó.
A. 1782 cm3
B. 1728 cm3
C. 576 cm3
D. 13824 cm3
Lời giải
Chiếc hộp hình lập phương gồm 5 hình vuông, mỗi hình vuông được sơn 1 mặt nên diện tích mỗi hình vuông là: 2880 : 5 = 576 (cm2)
Cạnh của hình lập phương bằng 24 cm, thể tích của hình lập phương bằng 243= 13924 (cm3)
Đáp án cần chọn là: B
Bài 16: Tính thể tích của một hình lập phương, biêt rằng đường chéo của hình lập phương bằng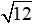 
cm.
A. 8 cm3
B. 4 cm3
C. 16 cm3
D. 18 cm3
Lời giải
Gọi a là cạnh của hình lập phương. Theo định lý Pitago ta có: AC2 = AB2 + BC2 = a2 + a2 suy ra AC2 + CC’2 = a2 + a2 + a2 = AC’2 = (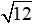)2 = 12
Từ đó a = 2 (cm). Thể tích của hình lập phương bằng 23 = 8 (cm3)
Đáp án cần chọn là: A
Bài 17: Tính thể tích của một hình lập phương, biết rằng đường chéo của hình lập phương bằng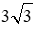 
cm.
Lời giải
Gọi a là cạnh của hình lập phương. Theo định lý Pitago ta có: AC’2 = AC2 + CC’2 = AB2 + BC2 + CC’2 = a2 + a2 + a2 = (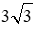)2 = 27 ⇔ 3a2 = 27 ⇔ a2 = 9 ⇔ a = 3
Từ đó a = 3 (cm). Thể tích của hình lập phương bằng 23 = 27 (cm3)
Đáp án cần chọn là: A
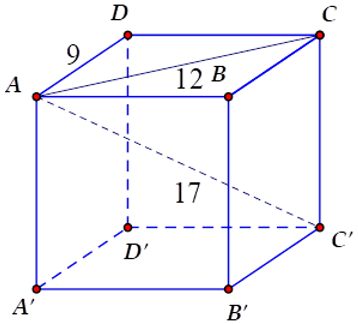
Bài 18: Một hình hộp chữ nhật có đường chéo lớn bằng 17cm, các kích thước của đáy bằng 9 cm và 12 cm. Tính thể tích của hình hộp chữ nhật đó.
A. 846 cm3
B. 864 cm3
C. 816 cm3
D. 186 cm3
Lời giải
Vì ABCD là hình chữ nhật nên AD = BC = 9 cm; AB = DC = 12 cm. Áp dụng định lý Pytago cho tam giác vuông ADC ta được:
Ta có CC' ⊥ (ABCD) nên CC' ⊥ CD
Áp dụng định lý Pytago cho tam giác vuông AC'C ta được:
Thể tích của hình hộp chữ nhât bằng
9.12.8 = 864 (cm3)
Đáp án cần chọn là: B
Bài 19: Một hình hộp chữ nhật có đường chéo lớn bằng 16,25 cm, các kích thước của đáy bằng 5 cm và 12 cm. Tính thể tích của hình hộp chữ nhật đó.
A. 585 cm3
B. 855 cm3
C. 785 cm3
D. 587 cm3
Lời giải
Vì ABCD là hình chữ nhật nên AD = BC = 5 cm; AB = DC = 12 cm.
Áp dụng định lý Pytago cho tam giác vuông ADC ta được:
Ta có: CC' ⊥ (ABCD) nên CC' ⊥ CD
Áp dụng định lý Pytago cho tam giác vuông AC'C ta được:
Thể tích của hình hộp chữ nhât bằng
9.12.9, 75 = 585 (cm3)
Đáp án cần chọn là: A
Bài 20: Một bể cá dạng hình hộp chữ nhật bằng kính (không nắp) có chiều dài 80 cm, chiều rộng 50 cm. Mực nước trong bể cao 35 cm. Người ra cho vào bể một hòn đá thì thể tích tăng 20000 cm3. Hỏi mực nước trong bể úc này cao bao nhiêu.
A. 40 cm
B. 30 cm
C. 60 cm
D. 50 cm
Lời giải
Thể tích phần bể chứa nước ban đầu là:
V = 8.50.35 = 140000 cm3
Sau khi cho vào một hòn đá thể tích tăng 20000 cm3. Vậy thể tích phần bể chứa nước lúc sau là:
V1 = V + 20000 = 140000 + 20000 = 160000 cm3
Vì chiều dài và chiều rộng bể nước không thay đổi nên sự thay đổi là do chiều cao mực nước thay đổi. Gọi chiều cao mực nước lúc sau là h cm. Ta có:
V = 80.50.h = 160000 ⇒ 
Đáp án cần chọn là: A
Bài 21: Một bể cá dạng hình hộp chữ nhật bằng kính (không nắp) có chiều dài 1 m, chiều rộng 70 cm, chiều cao 60 cm. Mực nước trong bể cao 30 cm. Người ra cho vào bể một hòn đá thì thể tích tăng 14000 cm3. Hỏi mực nước trong bể lúc này cao bao nhiêu.
A. 40 cm
B. 30 cm
C. 32 cm
D. 35 cm
Lời giải
Đổi 1m = 100 cm
Thể tích phần bể chứa nước ban đầu là:
V = 100.70.30 = 210000 cm3
Sau khi cho vào một hòn đá thể tích tăng 14000 cm3. Vậy thể tích phần bể chứa nước lúc sau là:
V1 = V + 14000 = 210000 + 14000 = 224000 cm3
Vì chiều dài và chiều rộng bể nước không thay đổi nên sự thay đổi là do chiều cao mực nước thay đổi. Gọi chiều cao mực nước lúc sau là h cm. Ta có:
V = 100.70.h = 224000 ⇒ 
Đáp án cần chọn là: C
Bài 22: Một người thuê sơn mặt trong và mặt ngoài của 1 cái thùng sắt không nắp dạng hình lập phương có cạnh 0, 8m. Biết giá tiền mỗi mét vuông là 15000 đồng. Hỏi người ấy phải trả bao nhiêu tiền?
A. 86000 đồng
B. 69000 đồng
C. 96600 đồng
D. 96000 đồng
Lời giải
Thùng sắt (không nắp) có dạng hình lập phương ⇒ Thùng sắt có 5 mặt bằng nhau.
Diện tích một thùng sắt là:
S = 0, 82 = 0, 64 m2
Ta có diện tích mặt trong thùng sắt bằng diện tích mặt ngoài thùng sắt. Vậy diện tích mặt trong và mặt ngoài thùng sắt là: Smt = Smn = 5S = 5. 0,64 = 3,2 m2
Số tiền người thuê sơn thùng sắt cần trả là: (Smt + Smn).15000 = (3, 2 + 3, 2).15000 = 6, 4. 15000 = 96000 đồng.
Đáp án cần chọn là: D
Bài 22: Một người thuê sơn mặt ngoài của 1 cái thùng sắt không nắp dạng hình lập phương có cạnh 0, 8m. Biết giá tiền mỗi mét vuông là 15000 đồng. Hỏi người ấy phải trả bao nhiêu tiền?
A. 48000 đồng
B. 64000 đồng
C. 45000 đồng
D. 96000 đồng
Lời giải
Thùng sắt (không nắp) có dạng hình lập phương ⇒ Thùng sắt có 5 mặt bằng nhau.
Diện tích một thùng sắt là:
S = 0, 82 = 0, 64 m2
Ta có diện tích mặt trong thùng sắt bằng diện tích mặt ngoài thùng sắt. Vậy diện tích mặt trong và mặt ngoài thùng sắt là: Smt = Smn = 5S = 5. 0,64 = 3,2 m2
Số tiền người thuê sơn thùng sắt cần trả là: 3, 2 .15000 = 48000 đồng.
Đáp án cần chọn là: A
