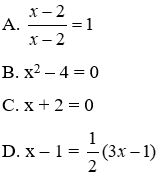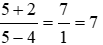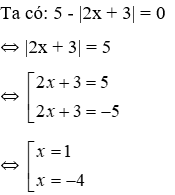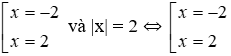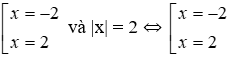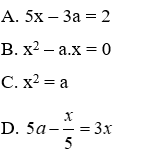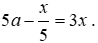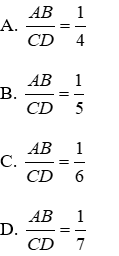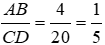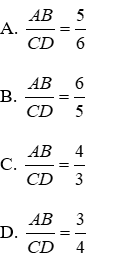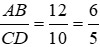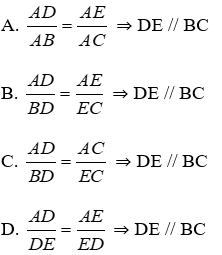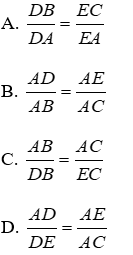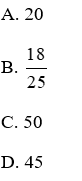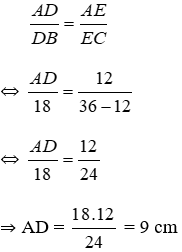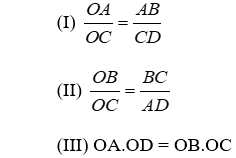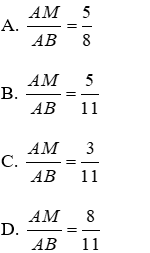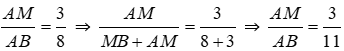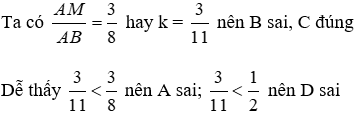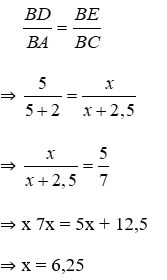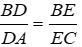500 bài tập trắc nghiệm Toán lớp 8 Học kì 2 có lời giải
500 bài tập trắc nghiệm Toán lớp 8 Học kì 2 có lời giải
Với bộ 500 bài tập trắc nghiệm Toán lớp 8 Học kì 2 có lời giải, chọn lọc sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 8.
Bài tập trắc nghiệm Toán lớp 8 Chương 3 Đại số có đáp án
- Trắc nghiệm Mở đầu về phương trình
- Trắc nghiệm Phương trình bậc nhất một ẩn và cách giải
- Trắc nghiệm Phương trình tích
- Trắc nghiệm Phương trình chứa ẩn ở mẫu
- Trắc nghiệm Giải bài toán bằng cách lập phương trình
- Trắc nghiệm Chương 3 Đại số 8 có đáp án
Bài tập trắc nghiệm Toán lớp 8 Chương 4 Đại số có đáp án
- Trắc nghiệm Liên hệ giữa thứ tự và phép cộng
- Trắc nghiệm Liên hệ giữa thứ tự và phép nhân
- Trắc nghiệm Bất phương trình bậc nhất một ẩn
- Trắc nghiệm Phương trình chứa dấu giá trị tuyệt đối
- Trắc nghiệm Chương 4 Đại số 8 có đáp án
Bài tập trắc nghiệm Toán lớp 8 Chương 3 Hình học có đáp án
- Trắc nghiệm Định lí Ta-lét trong tam giác
- Trắc nghiệm Tính chất đường phân giác của tam giác
- Trắc nghiệm Khái niệm hai tam giác đồng dạng
- Trắc nghiệm Trường hợp đồng dạng thứ nhất
- Trắc nghiệm Trường hợp đồng dạng thứ hai
- Trắc nghiệm Trường hợp đồng dạng thứ ba
- Trắc nghiệm Các trường hợp đồng dạng của tam giác vuông
- Trắc nghiệm Chương 3 Hình học 8 có đáp án
Bài tập trắc nghiệm Toán lớp 8 Chương 4 Hình học có đáp án
- Trắc nghiệm Hình hộp chữ nhật
- Trắc nghiệm Thể tích của hình hộp chữ nhật
- Trắc nghiệm Hình lăng trụ đứng
- Trắc nghiệm Hình chóp đều và hình chóp cụt đều
- Trắc nghiệm Chương 4 Hình học 8 có đáp án
Trắc nghiệm Mở đầu về phương trình có đáp án
Bài 1: Hai phương trình tương đương là hai phương trình có
A. Một nghiệm giống nhau
B. Hai nghiệm giống nhau
C. Tập nghiệm giống nhau
D. Tập nghiệm khác nhau
Lời giải
Hai phương trình tương đương là hai phương trình có cùng tập nghiệm
Đáp án cần chọn là: C
Bài 2: Chọn khẳng định đúng
A. Hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm
B. Hai phương trình được gọi là tương đương nếu chúng có cùng số nghiệm
C. Hai phương trình được gọi là tương đương nếu chúng có chung một nghiệm
D. Hai phương trình được gọi là tương đương nếu chúng cùng điều kiện xác định
Lời giải
Hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm
Đáp án cần chọn là: A
Bài 3: Số 
A. x - 1 =
B. 4x2 – 1 = 0
C. x2 + 1 = 5
D. 2x – 1 = 3
Lời giải
Thay x = 
+) 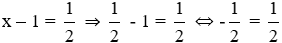

+) 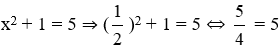

+) 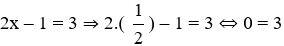

+) 4x2 – 1 = 0
⇒ 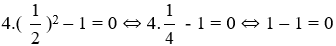

Đáp án cần chọn là: B
Bài 4: Phương trình nào sau đây nhận x = 2 làm nghiệm?
Lời giải
Đáp án A loại vì x = 2 không thỏa mãn điều kiện xác định
Đáp án B: 22 – 4 = 4 – 4 = 0 nên x = 2 là nghiệm của phương trình đáp án B.
Đáp án C: Dễ thấy 2 + 2 = 4 ≠ 0 nên x = 2 không là nghiệm của phương trình đáp án C
Đáp án D: Thay x = 2 ta được VT = 2 – 1 = 1 ≠ 
Đáp án cần chọn là: B
Bài 5: Chọn khẳng định đúng
A. 3 là nghiệm của phương trình x2 – 9 = 0
B. {3} là tập nghiệm của phương trình x2 – 9 = 0
C. Tập nghiệm của phương trình (x + 3)(x – 3) = x2 – 9 là Q
D. x = 2 là nghiệm duy nhất của phương trình x2 – 4 = 0
Lời giải
+ Ta có x2 – 9 = 0 ⇔ x2 = 9 ⇔ x = ±3. Nên x = 3 là nghiệm của phương trình x2 – 9 = 0 và tập nghiệm của phương trình là {3; -3}. Suy ra A đúng, B sai.
+ Xét (x + 3)(x – 3) = x2 – 9 ⇔ x2 – 9 = x2 – 9 (luôn đúng) nên tập nghiệm của phương trình là R, suy ra C sai.
+ Xét x2 – 4 = 0 ⇔ x2 = 4 ⇔ x = ±2 ⇒ phương trình có hai nghiệm x = 2; x = -2 nên D sai
Đáp án cần chọn là: A
Bài 6: Cho các mệnh sau:
(I) 5 là nghiệm của phương trình 2x – 3 = 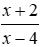
(II) Tập nghiệm của phương trình 7 – x = 2x – 8 là x = 5
(III) Tập nghiệm của phương trình 10 – 2x = 0 là S = {5}.
Số mệnh đề đúng là:
A. 1
B. 0
C. 2
D. 3
Lời giải
Mệnh đề (I): Thay x = 5 vào phương trình ta được VT = 2.5 – 3 = 7; VP =
Do đó VT = VP hay x = 5 là nghiệm của phương trình
Do đó (I) đúng
Mệnh đề (II): Sai do kí hiệu
7 – x = 2x – 8 ⇔ x = 5 nên phương trình có tập nghiệm S = {5}
Vậy có 2 mệnh đề đúng.
Đáp án cần chọn là: C
Bài 7: Phương trình nào sau đây vô nghiệm?
A. x – 1 = 0
B. 4x2 + 1 = 0
C. x2 – 3 = 6
D. x2 + 6x = -9
Lời giải
+) x – 1 = 0 ⇔ x = 1Ø
+) 4x2 + 1 = 0 ⇔ 4x2 = -1 (vô nghiệm vì 4x2 ≥ 0; Ɐx)
+) x2 – 3 = 6 ⇔ x2 = 9 ⇔ x = ± 3
+) x2 + 6x = -9 ⇔ x2 + 6x + 9 = 0 ⇔ (x + 3)2 = 0 ⇔ x + 3 = 0 ⇔ x = -3
Vậy phương trình 4x2 + 1 = 0 vô nghiệm
Đáp án cần chọn là: B
Bài 8: Phương trình nào sau đây vô nghiệm?
A. 2x – 1 = 0
B. -x2 + 4 = 0
C. x2 + 3 = -6
D. 4x2 +4x = -1
Lời giải
+) 2x – 1 = 0 ⇔ x = 
+) -x2 + 4 = 0 ⇔ x2 = 4 ⇔ x = ±2
+) x2 + 3 = -6 ⇔ x2 = -9 (vô nghiệm vì -9< 0)
+) 4x2 + 4x = -1 ⇔ 4x2 +4x + 1 = 0 ⇔ (2x + 1)2 = 0 ⇔ 2x + 1 = 0 ⇔ x = -
Đáp án cần chọn là: C
Bài 9: Tập nghiệm của phương trình 3x – 6 = x – 2 là
A. S = {2}
B. S = {-2}
C. S = {4}
D. S = Ø
Lời giải
Ta có 3x – 6 = x – 2 ⇔ 3x – x = -2 + 6 ⇔ 2x = 4 ⇔ x = 2
Tập nghiệm của phương trình là S = {2}
Đáp án cần chọn là: A
Bài 10: Phương trình 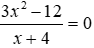
A. S = {±4}
B. S = {±2}
C. S = {2}
D. S = {4}
Lời giải
ĐKXĐ: x + 4 ≠ 0 ⇔ x ≠ -4
Phương trình ⇔ 3x2 – 12 = 0 ⇔ x2 = 4 ⇔ x = ±2 (tm)
Vậy tập nghiệm của phương trình là S = {±2}
Đáp án cần chọn là: B
Bài 11: Có bao nhiêu nghiệm của phương trình |x + 3| = 7?
A. 2
B. 1
C. 0
D. 4
Lời giải
Ta có: 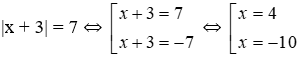
Vậy phương trình có hai nghiệm x = 4; x = -10
Đáp án cần chọn là: A
Bài 12: Số nghiệm của phương trình 5 - |2x + 3| = 0 là
A. 2
B. 1
C. 0
D. 4
Lời giải
Vậy phương trình có hai nghiệm x = 1; x = -4
Đáp án cần chọn là: A
Bài 13: Hai phương trình nào sau đây là hai phương trình tương đương?
A. x – 2 =4 và x + 1 = 2
B. x = 5 và x2 = 25
C. 2x2 – 8 = 0 và |x| = 2
D. 4 + x = 5 và x3 – 2x = 0
Lời giải
+) Xét x – 2 = 4 ⇔ x = 6 và x + 1 = 2 ⇔ x = 1 nên hai phương trình x – 2 =4 và x + 1 = 2 không tương đương
+) Xét phương trình x2 = 25 ⇔ x = ±5 nên phương trình x2 = 25 có hai nghiệm. Suy ra hai phương trình x = 5 và x2 = 25 không tương đương.
+) Xét phương trình 4 + x = 5 ⇔ x = 1, mà x = 1 không là nghiệm của phương trình x3 – 2x = 0 (vì 13 – 2.1= -1 ≠ 0) nên hai phương trình 4 + x = 5 và x3 – 2x = 0 không tương đương.
+) Xét phương trình 2x2 – 8 = 0 ⇔ 2x2 = 8 ⇔ x2 = 4 ⇔
Nhận thấy hai phương trình trên có cùng tập nghiệm {2; -2} nên chúng tương đương.
Đáp án cần chọn là: C
Bài 14: Số cặp phương trình tương đương trong các cặp phương trình sau là:
(I) x – 2 =4 và x + 1 = 2
(II) x = 5 và x2 = 25
(III) 2x2 – 8 = 0 và |x| = 2
(IV) 4 + x = 5 và x3 – 2x = 0
A. 1
B. 2
C. 3
D. 4
Lời giải
+) Xét x – 2 = 4 ⇔ x = 6 và x + 1 = 2 ⇔ x = 1 nên hai phương trình x – 2 =4 và x + 1 = 2 không tương đương
+) Xét phương trình x2 = 25 ⇔ x = ±5 nên phương trình x2 = 25 có hai nghiệm. Suy ra hai phương trình x = 5 và x2 = 25 không tương đương.
+) Xét phương trình 4 + x = 5 ⇔ x = 1, mà x = 1 không là nghiệm của phương trình x3 – 2x = 0 (vì 13 – 2.1= -1 ≠ 0) nên hai phương trình 4 + x = 5 và x3 – 2x = 0 không tương đương.
+) Xét phương trình 2x2 – 8 = 0 ⇔ 2x2 = 8 ⇔ x2 = 4 ⇔
Nhận thấy hai phương trình trên có cùng tập nghiệm {2; -2} nên chúng tương đương.
Vậy chỉ có 1 cặp phương trình tương đương trong các cặp đã cho
Đáp án cần chọn là: A
Bài 15: Phương trình nào dưới đây nhận x = a (a là hằng số khác 0 và 1) làm nghiệm
Lời giải
Thay x = a vào từng phương trình ta được
+) 5.a – 3a = 2 ⇔ 2a = 2 ⇔ a = 1 (loại) nên x = a không là nghiệm của phương trình 5x – 3a = 2
+) a2 = a ⇔ 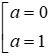
+) 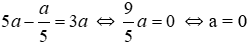
+) a2 – a.a = a2 – a2 = 0 nên x = a là nghiệm của phương trình x2 – a.x = 0
Đáp án cần chọn là: B
Trắc nghiệm Định lí Ta-lét trong tam giác có đáp án
Bài 1: Viết tỉ số cặp đoạn thẳng có độ dài như sau: AB = 4dm, CD = 20 dm
Lời giải
AB = 4dm, CD = 20 dm ⇒
Vậy 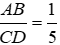
Đáp án cần chọn là: B
Bài 2: Viết tỉ số cặp đoạn thẳng có độ dài như sau: AB = 12cm, CD = 10 cm
Lời giải
AB = 12cm, CD = 10 cm ⇒
Vậy 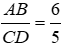
Đáp án cần chọn là: B
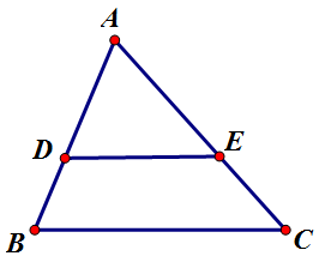
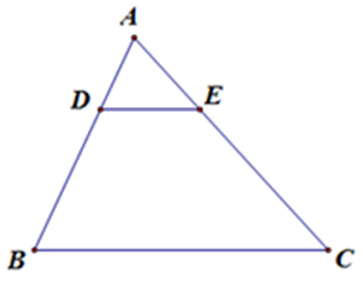
Bài 3: hãy chọn câu sai. Cho hình vẽ với AB < AC:
Lời giải
Theo định lý đảo của định lý Ta-lét. Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Nên D sai.
Đáp án cần chọn là: D
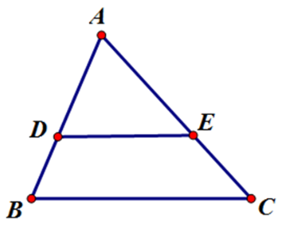
Bài 4: Cho hình vẽ. Điều kiện nào sau đây không suy ra được DE // BC?
Lời giải
Theo định lý đảo của định lý Ta-lét. Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Dễ thấy, từ các điều kiện 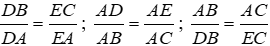
Chỉ có D sai.
Đáp án cần chọn là: D
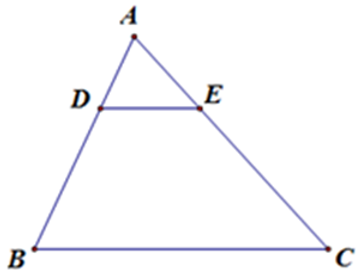
Bài 5: Cho hình vẽ, trong đó DE // BC, AD = 12, DB = 18, CE = 30. Độ dài AC bằng:
Lời giải
Vì DE // BC, theo định lý Ta-lét ta có:
Nên AC = AE + EC = 50 cm
Đáp án cần chọn là: C
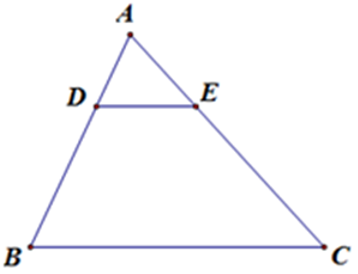
Bài 6: Cho hình vẽ, trong đó DE // BC, AE = 12, DB = 18, CA = 36. Độ dài AB bằng:
A. 30
B. 36
C. 25
D. 27
Lời giải
Vì DE // BC, theo định lý Ta-lét ta có:
Nên AB = AD + DB = 9 + 18 = 27 cm
Đáp án cần chọn là: D
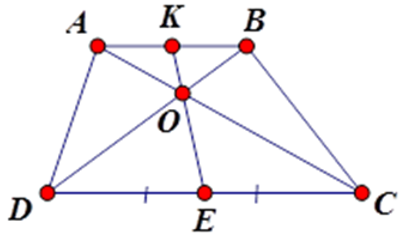
Bài 7: Chọn câu trả lời đúng:
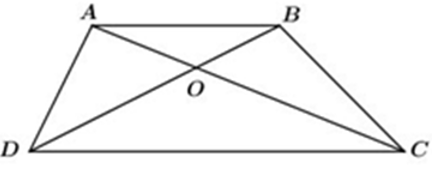
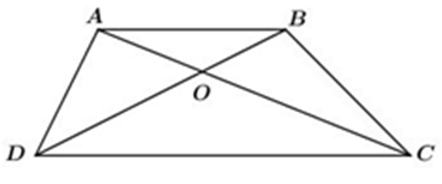
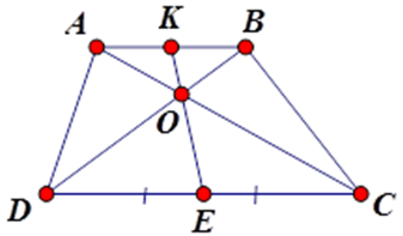
Cho hình thang ABCD (AB // CD), O là giao điểm của AC và BD. Xét các khẳng định sau:
A. Chỉ có (I) đúng
B. Chỉ có (II) đúng
C. Cả (I) và (II) đúng
D. Cả (I) và (II) sai
Lời giải
Đáp án cần chọn là: A
Bài 8: Chọn câu trả lời đúng:
Cho hình thang ABCD (AB // CD), O là giao điểm của AC và BD. Xét các khẳng định sau:
Số khẳng định đúng trong các khẳng định trên là:
A. 1
B. 2
C. 0
D. 3
Lời giải
Vậy có 2 khẳng định đúng.
Đáp án cần chọn là: B
Bài 9: Cho biết M thuộc đoạn thẳng AB thỏa mãn 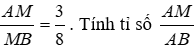
Lời giải
Đáp án cần chọn là: C
Bài 10: Cho biết M thuộc đoạn thẳng AB thỏa mãn 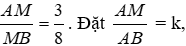
Lời giải
Đáp án cần chọn là: C
Bài 11: Cho hình vẽ, trong đó AB // CD và DE = EC. Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
A. 1
B. 2
C. 3
D. 4
Lời giải
Đáp án cần chọn là: C
Bài 12: Cho hình vẽ, trong đó AB // CD và DE = EC. Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
A. 1
B. 2
C. 3
D. 4
Lời giải
Theo định lý Ta-lét:
Vậy cả 4 khẳng định đã cho đều đúng.
Đáp án cần chọn là: D
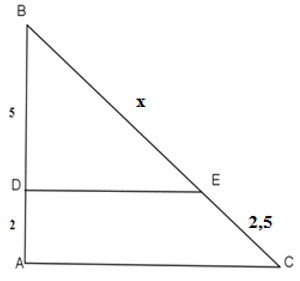
Bài 13: Chọn câu trả lời đúng. Cho hình bên, biết DE // AC, tìm x:
A. x = 6,5
B. x = 6,25
C. x = 5
D. x = 8
Lời giải
Vì DE // AC, áp dụng định lý Talet, ta có:
Đáp án cần chọn là: B
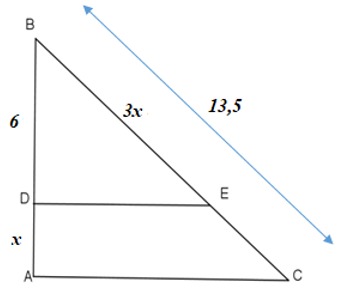
Bài 14: Chọn câu trả lời đúng. Cho hình bên biết ED ⊥ AB, AC ⊥ AB, tìm x:
A. x = 3
B. x = 2,5
C. x = 2
D. x = 4
Lời giải
Ta có: ED ⊥ AB, AC ⊥ AB ⇒ DE // AC (từ vuông góc đến song song), áp dụng định lý Talet, ta có:
⇔ x2 + 6x – 27 = 0
Vậy x = 3
Đáp án cần chọn là: A
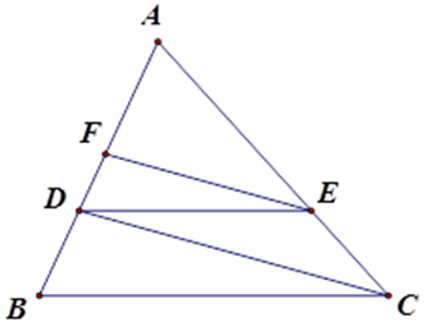
Bài 15: Cho tam giác ABC có AB = 9cm, điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE song song với BC (E Є AC), kẻ EF song song với CD (F Є AB). Tính độ dài AF.
A. 6 cm
B. 5 cm
C. 4 cm
D. 7 cm
Lời giải
Áp dụng định lý Ta-lét:
Đáp án cần chọn là: C