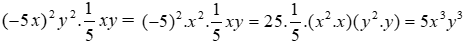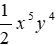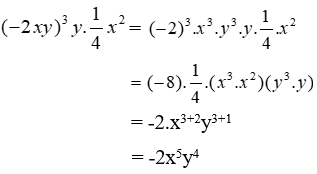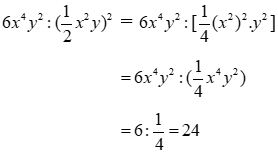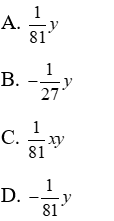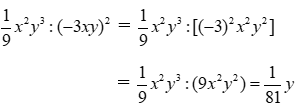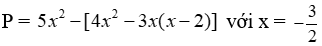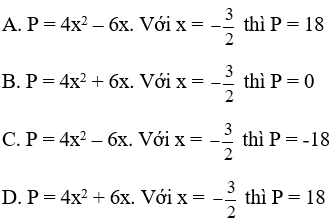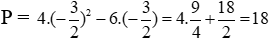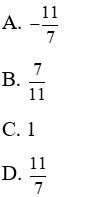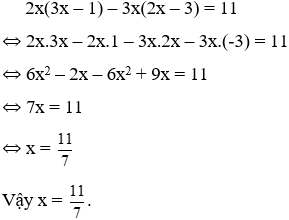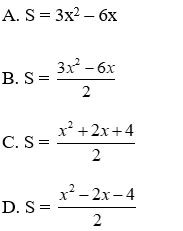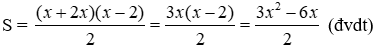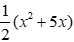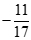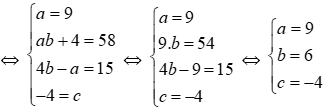Trắc nghiệm Nhân đơn thức với đa thức có đáp án - Toán lớp 8
Trắc nghiệm Nhân đơn thức với đa thức có đáp án
Với bộ bài tập Trắc nghiệm Nhân đơn thức với đa thức Toán lớp 8 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 8.

Bài 1: Tích 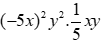
A. 5x3y3
B. -5x3y3
C. -x3y3
D. x3y2
Lời giải
Ta có:
Đáp án cần chọn là: A
Bài 2: Tích 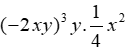
A. -2x4y5
B.
C. 2x5y4
D. -2x5y4
Lời giải
Ta có:
Đáp án cần chọn là: D
Bài 3: Thu gọn 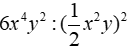
A. 12
B. 24
C. 24x2y
D. 12x2y
Lời giải
Ta có:
Đáp án cần chọn là: B
Bài 4: Thu gọn biểu thức 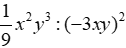
Lời giải
Ta có:
Đáp án cần chọn là: A
Bài 5: Kết quả của phép tính (ax2 + bx – c).2a2x bằng
A. 2a4x3 + 2a2bx2 – 2a2cx
B. 2a3x3 + bx – c
C. 2a4x2 + 2a2bx2 – a2cx
D. 2a3x3 + 2a2bx2 – 2a2cx
Lời giải
Ta có: (ax2 + bx – c).2a2x = 2a2x.(ax2 + bx – c)
= 2a2x.ax2 + 2a2x.bx – 2a2x.c
= 2a3x3 + 2a2bx2 – 2a2cx
Đáp án cần chọn là: D
Bài 6: Tích 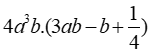
A. 12a4b2 – 4a3b + a3b
B. 12a4b2 – 4a3b2 + a3b
C. 12a3b2 + 4a3b2 + 4a3b
D. 12a4b2 – 4a3b2 + a3b
Lời giải
Ta có: 12a4b2 – 4a3b + a3b = 4a3b.3ab – 4a3b.b + 4a3b.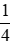
= 12a4b2 – 4a3b2 + a3b
Đáp án cần chọn là: D
Bài 7: Kết quả của phép tính -4x2(6x3 + 5x2 – 3x + 1) bằng
A. 24x5 + 20x4 + 12x3 – 4x2
B. -24x5 – 20x4 + 12x3 + 1
C. -24x5 – 20x4 + 12x3 – 4x2
D. -24x5 – 20x4 – 12x3 + 4x2
Lời giải
Ta có: -4x2(6x3 + 5x2 – 3x + 1)
= (-4x2).6x3 + (-4x2).5x2 + (-4x2).(-3x) + (-4x2).1
= -24x5 – 20x4 + 12x3 – 4x2
Đáp án cần chọn là: C
Bài 8: Tích ( x- y)(x + y) có kết quả bằng
A. x2 – 2xy + y2
B. x2 + y2
C. x2 – y2
D. x2 + 2xy + y2
Lời giải
Ta có ( x- y)(x + y) = x.x + x.y – x.y – y.y = x2 – y2
Đáp án cần chọn là: C
Bài 9: Tích (2x – 3)(2x + 3) có kết quả bằng
A. 4x2 + 12x+ 9
B. 4x2 – 9
C. 2x2 – 3
D. 4x2 + 9
Lời giải
Ta có (2x – 3)(2x + 3) = 2x.2x + 2x.3 – 3.2x + (-3).3
= 4x2 + 6x – 6x – 9 = 4x2 – 9
Đáp án cần chọn là: B
Bài 10: Giá trị của biểu thức P = -2x2y(xy + y2) tại x = -1; y = 2 là
A. 8
B. -8
C. 6
D. -6
Lời giải
Thay x = -1; y = 2 vào biểu thức P = -2x2y(xy + y2) ta được
P = -2.(-1)2.2[(-1).2 + 22] = -4.2 = -8
Đáp án cần chọn là: B
Bài 11: Chọn câu sai.
A. Giá trị của biểu thức ax(ax + y) tại x = 1; y = 0 là a2.
B. Giá trị của biểu thức ay2(ax + y) tại x = 0; y = 1 là (1 + a)2.
C. Giá trị của biểu thức -xy(x - y) tại x = -5; y = -5 là 0.
D. Giá trị của biểu thức xy(-x - y) tại x = 5; y = -5 là 0.
Lời giải
+) Thay x = 1; y = 0 vào biểu thức ax(ax + y) ta được
a.1(a.1+0) = a.a = a2 nên phương án A đúng
+) Thay x = 0, y = 1 vào biểu thức ay2(ax + y) ta được
a.12(a.0+1) = a.1 = a nên phương án B sai.
+) Thay x = −5, y = −5 vào biểu thức −xy(x − y) ta được
−(−5)(−5)[−5−(−5)] = −25.0 = 0 nên phương án C đúng
+) Thay x = 5, y = −5 vào biểu thức xy(−x − y) ta được
5.(−5)[−5−(−5)] = −25.0 = 0 nên phương án D đúng.
Đáp án cần chọn là: B
Bài 12: Rút gọn và tính giá trị của biểu thức
Lời giải
Ta có P = 5x2 - [4x2 - 3x(x - 2)]
= 5x2 – (4x2 – 3x2 + 6x) = 5x2 – (x2 + 6x)
= 5x2 – x2 – 6x = 4x2 – 6x
Thay 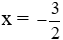
Vậy P = 4x2 – 6x. Với 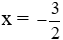
Đáp án cần chọn là: A
Bài 13: Chọn câu đúng.
A. (x2 – 1)(x2 + 2x) = x4 – x3 – 2x
B. (x2 – 1)(x2 + 2x) = x4 – x2 – 2x
C. (x2 – 1)(x2 + 2x) = x4 + 2x3 – x2 – 2x
D. (x2 – 1)(x2 + 2x) = x4 + 2x3 – 2x
Lời giải
Ta có: (x2 – 1)(x2 + 2x) = x2.x2 + x2.2x – 1.x2 – 1.2x
= x4 + 2x3 – x2 – 2x
Đáp án cần chọn là: C
Bài 14: Chọn câu đúng.
A. (x – 1)(x2 + x + 1) = x3 – 1
B. (x – 1)(x + 1) = 1 – x2
C. (x + 1)(x – 1) = x2 + 1
D. (x2 + x + 1)(x – 1) = 1 – x2
Lời giải
Ta có
+) (x – 1)(x + 1) = x.x + x – x – 1 = x2 – 1 nên phương án B sai, C sai
+) (x – 1)(x2 + x + 1)
= x.x2 + x.x + x.1 – x2 – x – 1
= x3 + x2 + x – x2 – x – 1 = x3 – 1 nên phương án D sai, A đúng
Đáp án cần chọn là: A
Bài 15: Chọn câu đúng.
A. (2x – 1)(3x2 -7x + 5) = 6x3 – 17x2 + 17x – 1
B. (2x – 1)(3x2 -7x + 5) = 6x3 – 4x2 + 4x – 5
C. (2x – 1)(3x2 -7x + 5) = 6x3 – 17x2 + 10x – 5
D. (2x – 1)(3x2 -7x + 5) = 6x3 – 17x2 + 17x – 5
Lời giải
Ta có (2x – 1)(3x2 -7x + 5) = 2x.3x2 + 2x.(-7x) + 2x.5 – 3x2 – (-7x) – 1.5
= 6x3 – 14x2 + 10x – 3x2 + 7x – 5
= 6x3 – 17x2 + 17x – 5
Đáp án cần chọn là: D
Bài 16: Cho 4(18 – 5x) – 12(3x – 7) = 15(2x – 16) – 6(x + 14). Kết quả x bằng:
A. 8
B. -8
C. 6
D. -6
Lời giải
Ta có
4(18 – 5x) – 12(3x – 7) = 15(2x – 16) – 6(x + 14)
⇔ 72 – 20x – 36x + 84 = 30x – 240 – 6x – 84
⇔ -56x + 156 = 24x – 324
⇔ 24x + 56x = 156 +324
⇔ 80x = 480
⇔ x = 6
Vậy x = 6
Đáp án cần chọn là: C
Bài 17: Cho 2x(3x – 1) – 3x(2x – 3) = 11. Kết quả x bằng:
Lời giải
Ta có:
Đáp án cần chọn là: D
Bài 18: Cho biểu thức P = 2x(x2 – 4) + x2(x2 – 9). Hãy chọn câu đúng:
A. Giá trị của biểu thức P tại x = 0 là 1
B. Giá trị của biểu thức P tại x = 2 là -20
C. Giá trị của biểu thức P tại x = -2 là 30
D. Giá trị của biểu thức P tại x = -9 là 0
Lời giải
Thay x = 0 vào P ta được
P = 2.0(02 – 4) + 02(02 – 9) = 0 nên A sai.
Thay x = -2 vào P ta được
P = 2.(-2).((-2)2 – 4) + (-2)2.((-2)2 – 9) = -20 nên C sai.
Thay x = -9 vào P ta được
P = 2.(-9).((-9)2 – 4) + (-9)2.((-9)2 – 9) = 4446 nên D sai.
Thay x = 2 vào P ta được
P = 2.2.(22 – 4) + 22(22 – 9) = 4.0 + 4.(-5) = -20 nên B đúng
Đáp án cần chọn là: B
Bài 19: Cho biểu thức M = x2(3x – 2) + x(-3x2 + 1). Hãy chọn câu đúng
A. Giá trị của biểu thức M tại x = 0 là 1
B. Giá trị của biểu thức M tại x = 1 là 1
C. Giá trị của biểu thức M tại x = -2 là -6
D. Giá trị của biểu thức M tại x = 3 là -15
Lời giải
Ta có M = x2(3x – 2) + x(-3x2 + 1) = x2.3x + x2.(-2) + x.(-3x2) + x.1
= 3x3 – 2x2 – 3x3 + x = -2x2 + x
Thay x = 0 vào M = -2x2 + x ta được
M = -2.02 + 0 = 0 nên A sai.
Thay x = 1 vào M = -2x2 + x ta được
M = -2.12 + 1 = -1 nên B sai
Thay x = -2 vào M = -2x2 + x ta được
M = -2.(-2)2 + (-2) = -10 nên C sai.
Thay x = 3 vào M = -2x2 + x ta được
M = -2.32 + 3 = -15 nên D đúng
Đáp án cần chọn là: D
Bài 20: Cho biểu thức A = x(x + 1) + (1 – x)(1 + x) – x. Khẳng định nào sau đây là đúng.
A. A = 2 – x
B. A < 1
C. A > 0
D. A > 2
Lời giải
Ta có A = x(x + 1) + (1 – x)(1 + x) – x = x2 + x + 1 + x – x – x2 – x = 1
Suy ra A = 1 > 0
Đáp án cần chọn là: C
Bài 21: Cho bểu thức B = (2x – 3)(x +7) – 2x(x + 5) – x. Khẳng định nào sau đây là đúng.
A. B = 21 – x
B. B < -1
C. B > 0
D. 10 < B < 20
Lời giải
Ta có B = (2x – 3)(x +7) – 2x(x + 5) – x
= 2x.x + 2x.7 – 3.x – 3.7 – 2x.x – 2x.5 – x
= 2x2 + 14x – 2x – 21 – 2x2 – 10x – x
= (2x2 – 2x2) + (14x – 3x – 10x – x) – 21 = -21
Đáp án cần chọn là: B
Bài 22: Cho biểu thức C = x(y + z) – y(z + x) – z(x – y). Chọn khẳng định đúng.
A. Biểu thức C không phụ thuộc vào x; y; z
B. Biểu thức C phụ thuộc vào cả x; y; z
C. Biểu thức C chỉ phụ thuộc vào y
D. Biểu thức C chỉ phụ thuộc vào z
Lời giải
Ta có C = x(y + z) – y(z + x) – z(x – y)
= xy + xz – yz – xy – zx + xy
= (xy – xy) + (zy – zy) + (xz – zx) = 0
Nên C không phụ thuộc vào x; y; z
Đáp án cần chọn là: A
Bài 23: Cho biểu thức D = x(x – y) + y(x + y) – (x + y)(x – y) – 2y2. Chọn khẳng định đúng.
A. Biểu thức D có giá trị là một số dương
B. Biểu thức D có giá trị là một số âm
C. Biểu thức D có giá trị phụ thuộc vào y, x
D. Biểu thức D có giá trị là 0
Lời giải
Ta có
D = x(x – y) + y(x + y) – (x + y)(x – y) – 2y2
= x2 – xy + xy + y2 – (x2 – xy + xy – y2) – 2y2
= x2 + y2 – (x2 – y2) – 2y2
= x2 + y2 – x2 + y2 – 2y2
= (x2 – x2) + (y2 + y2 – 2y2)
= 0
Nên D = 0
Đáp án cần chọn là: D
Bài 24: Biểu thức D = x(x2n-1 + y) – y(x + y2n-1) + y2n – x2n + 5, D có giá trị là:
A. 2y2n
B. -5
C. x2n
D. 5
Lời giải
Ta có
D = x(x2n-1 + y) – y(x + y2n-1) + y2n – x2n + 5
= x.x2n-1 + x.y – y.x – y.y2n-1 + y2n – x2n + 5
= x2n + xy – xy – y2n + y2n – x2n + 5
= (x2n – x2n) + (xy – xy) + (y2n – y2n) + 5
= 0 + 0 + 0 + 5 = 5
Đáp án cần chọn là: D
Bài 25: Rút gọn biểu thức N = 2xn(3xn+2 – 1) – 3xn+2(2xn – 1) ta được
A. N = 2xn + 3xn+2
B. N = -2xn – 3xn+2
C. N = -2xn + 3xn+2
D. N = -2xn + xn+2
Lời giải
Ta có N = 2xn(3xn+2 – 1) – 3xn+2(2xn – 1)
N = 2xn(3xn+2 – 1) – 3xn+2(2xn – 1)
= 2xn.3xn+2 – 2xn.1 – 3xn+2.2xn – 3xn+2.(-1)
= 6xn+n+2 – 2xn – 6.xn+2+n + 3xn+2
= 6x2n+2 – 6x2n+2 – 2xn + 3xn+2
= – 2xn + 3xn+2
Vậy N = – 2xn + 3xn+2
Đáp án cần chọn là: C
Bài 26: Cho hai số tự nhiên n và m. Biết rằng n chia 5 dư 1, m chia 5 dư 4. Hãy chọn câu đúng:
A. m.n chia 5 dư 1
B. m – n chia hết cho 5
C. m + n chia hết cho 5
D. m.n chia 5 dư 3
Lời giải
Ta có n chia 5 dư 1 nên n = 5p + 1 (0 < p < n; p ∈ N); m chia 5 dư 4 nên
m = 5q + 4 (0 < q < m ; q ∈ N)
Khi đó m.n = (5p + 1)(5q + 4) = 25pq + 20p + 5q + 4 = 5(5pq + 4p + q) + 4
Mà 5(5pq + 4p + q) ⋮ nên m.n chia 5 dư 4 , phương án A sai, D sai.
Ta có m – n = 5q + 4 − (5p + 1) = 5q − 5p + 3
Mà 5p ⋮ 5; 5q ⋮ 5 nên m − n chia 5 dư 3 , phương án B sai.
Ta có m + n = 5q + 4 + 5p + 1 = 5q + 5p + 5 = 5(q + p + 1) ⋮ 5 nên C đúng.
Đáp án cần chọn là: C
Bài 27: Cho hai a, b là những số nguyên và (2a + b) ⋮ 13; (5a – 4b) ⋮ 13. Hãy chọn câu đúng:
A. a – 6b chia hết cho 13
B. a – 6b chia cho 13 dư 6
C. a – 6b chia cho 13 dư 1
D. a – 6b chia cho 13 dư 3
Lời giải
Ta có (2a + b) ⋮ 13; (5a – 4b) ⋮ 13, suy ra 2(2a + b) ⋮ 13
Từ đó ta có (5a – 4b) - 2(2a + b) ⋮ 13 hay a – 6b ⋮ 13
Đáp án cần chọn là: A
Bài 28: Cho hình thang có đáy lớn gấp đôi đáy nhỏ, đáy nhỏ lớn hơn chiều cao 2 đơn vị. Biểu thức tính diện tích hình thang là
Lời giải
Gọi x (x > 2) là độ dài đáy nhỏ của hình thang
Theo giả thiết ta có độ dài đáy lớn là 2x, chiều cao của hình thang là x – 2
Diện tích hình thang là
Đáp án cần chọn là: B
Bài 29: Cho hình chữ nhật có chiều dài lớn hơn chiều rộng là 5 đơn vị. Biểu thức tính diện tích hình chữ nhật là:
A. S = x2 + 5x
B. S =
C. S = 2x + 5
D. S = x2 – 5x
Lời giải
Gọi x ( x > 0) là chiều rộng của hình chữ nhật
Theo giả thiết ta có chiều dài hình chữ nhật là x + 5
Diện tích hình chữ nhật là S = x(x + 5) = x2 + 5x (đvdt)
Đáp án cần chọn là: A
Bài 30: Giá trị của biểu thức M = x(x3 + x2 – 3x – 2)- (x2 – 2)(x2 + x – 1) là
A. 2
B. 1
C. – 1
D. – 2
Lời giải
Ta có
M = x(x3 + x2 – 3x – 2)- (x2 – 2)(x2 + x – 1)
= x.x3 + x.x2 – 3x.x – 2.x – (x2.x2 + x2.x – x2 – 2x2 – 2x + 2)
= x4 + x3 – 3x2 – 2x – (x4 + x3 – 3x2 – 2x + 2)
= x4 + x3 – 3x2 – 2x – x4 – x3 + 3x2 + 2x – 2
= - 2
Vậy M = -2
Đáp án cần chọn là: D
Bài 31: Giá trị của biểu thức P = (3x – 1)(2x + 3) – (x – 5)(6x – 1) – 38x là
A. P = -8
B. P = 8
C. P = 2
D. P = -2
Lời giải
Ta có
P = (3x – 1)(2x + 3) – (x – 5)(6x – 1) – 38x
= 3x.2x + 3x.3 – 1.2x – 1.3 – (x.6x – x – 5.6x – 5.(-1)) – 38x
= 6x2 + 9x – 2x – 3 – 6x2 + x + 30x – 5 – 38x
= (6x2 – 6x2) + (9x – 2x + x + 30x – 38x) – 3 – 5
= -8
Vậy P = -8
Đáp án cần chọn là: A
Bài 32: Cho A = (3x + 7)(2x + 3) – (3x – 5)(2x + 11); B = x(2x + 1) – x2(x + 2) + x3 – x + 3. Chọn khẳng định đúng
A. A = B
B. A = 25B
C. A = 25B + 1
D. A = B/2
Lời giải
A = (3x + 7)(2x + 3) – (3x – 5)(2x + 11)
= 3x.2x + 3x.3 + 7.2x + 7.3 – (3x.2x + 3x.11 – 5.2x – 5.11)
= 6x2 + 9x + 14x + 21 – (6x2 + 33x – 10x – 55)
= 6x2 + 23x + 21 – 6x2 – 33x + 10x + 55 = 76
B = x(2x + 1) – x2(x + 2) + x3 – x + 3
= x.2x + x – (x2.x + 2x2) + x3 – x + 3
= 2x2 + x – x3 – 2x2 + x3 – x + 3 = 3
Từ đó ta có A = 76; B = 3 mà 76 = 25.3 + 1 nên A = 25B + 1
Đáp án cần chọn là: C
Bài 33: Cho M = -3(x – 4)(x – 2) + x(3x – 18) – 25; N = (x – 3)(x + 7) – (2x – 1)(x + 2) + x(x – 1). Chọn khẳng định đúng.
A. M – N = 30
B. M – N = -30
C. M – N = 20
D. M – N = -68
Lời giải
M = -3(x – 4)(x – 2) + x(3x – 18) – 25
= -3(x2 – 2x – 4x + 8) + x.3x + x.(-18) – 25
= -3x2 + 6x + 12x – 24 + 3x2 – 18x – 25
= (-3x2 + 3x2) + (6x + 12x – 18x) – 24 – 25
= -49
N = (x – 3)(x + 7) – (2x – 1)(x + 2) + x(x – 1)
= x.x + x.7 – 3.x – 3.7 – (2x.x + 2x.2 – x – 1.2) + x.x + x.(-1)
= x 2 + 7x – 3x – 21 – 2x2 – 4x + x + 2 + x2 – x
= (x2 – 2x2 + x2) + (7x – 3x – 4x + x – x) – 21 + 2
= -19
Vậy M = -49; N = -19 ⇒ M – N = -30
Đáp án cần chọn là: B
Bài 34: Gọi x là giá trị thỏa mãn 5(3x + 5) – 4(2x – 3) = 5x + 3(2x – 12) + 1. Khi đó
A. x > 18
B. x < 17
C. 17 < x < 19
D. 18 < x < 20
Lời giải
Ta có
5(3x + 5) − 4(2x − 3) = 5x + 3(2x − 12) + 1
⇔ 15x + 25 − 8x + 12 = 5x + 6x – 36 + 1
⇔ 7x + 37 = 11x − 35
⇔ 4x = 72
⇔ x = 18
Vậy x = 18.
Suy ra 17 < x < 19 nên chọn C.
Đáp án cần chọn là: C
Bài 35: Gọi x là giá trị thỏa mãn (3x – 4)(x – 2) = 3x(x – 9) – 3. Khi đó
A. x < 0
B. x < -1
C. x > 2
D. x > 0
Lời giải
Ta có (3x – 4)(x – 2) = 3x(x – 9) – 3
⇔ 3x.x+ 3x.(-2) – 4.x – 4.(-2) = 3x.x + 3x.(-9) – 3
⇔ 3x2 – 6x -4x + 8 = 3x2 – 27x – 3
⇔ 17x = -11 ⇔ x =
Vậy x =
Đáp án cần chọn là: A
Bài 36: Tính giá trị của biểu thức
P = x10 – 13x9 + 13x8 – 13x7 + … - 13x + 10 tại x = 12
A. P = -2
B. P = 2
C. P = 4
D. P = 0
Lời giải
Ta có
P = x10 – 13x9 + 13x8 – 13x7 + … - 13x + 10
= x10 – 12x9 – x9 + 12x8 + x8 – 12x7 – x7 + 12x6 + … +x2 – 12x – x + 10
= x9(x – 12) – x8(x – 12) + x7(x – 12) - … + x(x – 12) – x + 10
Thay x = 12 vào P ta được
P = 129.(12 – 12) – 128(12 – 12) + 127(12 – 12) - … + 12(12 – 12) – 12 + 10
= 0 + … + 0 – 2 = -2
Vậy P = -2
Đáp án cần chọn là: A
Bài 37: Tính bằng cách hợp lý giá trị của A = x5 – 70x4 – 70x3 – 70x2 – 70x + 29 tại x = 71.
A. A = 50
B. A = -100
C. A = 100
D. A = -50
Lời giải
Ta có
A = x5 – 70x4 – 70x3 – 70x2 – 70x + 29
= x5 – 71x4 + x4 – 71x3 + x3 – 71x2 + x2 – 71x + x – 71 + 100
= x4(x – 71) + x3(x – 71) + x2(x – 71) + x(x – 71) + (x – 71) + 100
Vì x = 71 nên x – 71 = 0, thay x – 71 = 0 vào A ta đươc
A = x4.0 + x3.0 + x2.0 + x.0 + 0 + 100 = 100
Vậy A = 100
Đáp án cần chọn là: C
Bài 38: Xác định hệ số a, b, c biết rằng với mọi giá trị của x thì (ax + 4)(x2 + bx – 1) = 9x3 + 58x2 + 15x + c
A. a = 9, b = -4, c = 6
B. a = 9, b = 6, c = -4
C. a = 9, b = 6, c = 4
D. a = -9, b = -6, c = -4
Lời giải
Ta có T = (ax + 4)(x2 + bx – 1)
= ax.x2 + ax.bx + ax.(-1) + 4.x2 + 4.bx + 4.(-1)
= ax3 + abx2 – ax + 4x2 + 4bx – 4
= ax3 + (abx2 + 4x2) + (4bx – ax) – 4
= ax3 + (ab + 4)x2 + (4b – a)x – 4
Theo bài ra ta có (ax + 4)(x2 + bx – 1) = 9x3 + 58x2 + 15x + c đúng với mọi x
⇔ ax3 + (ab + 4)x2 + (4b – a)x – 4 = 9x3 + 58x2 + 15x + c đúng với mọi x.
Vậy a = 9, b = 6, c = -4
Đáp án cần chọn là: B
Bài 39: Cho x2 + y2 = 2, đẳng thức nào sau đây đúng?
A. 2(x + 1)(y + 1) = (x + y)(x + y – 2)
B. 2(x + 1)(y + 1) = (x + y)(x + y + 2)
C. 2(x + 1)(y + 1)(x + y) = 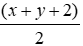
D. (x + 1)(y + 1) = (x + y)(x + y + 2)
Lời giải
Ta có 2(x + 1)(y + 1) = 2(xy + x + y + 1) = 2xy + 2x + 2y + 2
Thay x2 + y2 = 2 ta được
2xy + 2x + 2y + x2+ y2
= (x2+ xy + 2x) + (y2 + xy + 2y)
= x(x + y + 2) + y(x + y + 2) = (x + y)(x + y +2)
Từ đó ta có 2(x + 1)(y + 1) = (x + y)(x + y + 2)
Đáp án cần chọn là: B
Bài 40: Cho biết (x + y)(x + z) + (y + z)(y + x) = 2(z + x)(z + y). Khi đó
A. z2 = 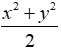
B. z2 = x2 + y2
C. z2 = 2(x2 + y2)
D. z2 = x2 – y2
Lời giải
Ta có (x + y)(x + z) + (y + z)(y + x) = 2(z + x)(z + y).
⇔ x.x. + xz + yx + yz + y.y + yx + zy + zx = 2(z.z + zy + zx + xy)
⇔ x2 + 2xz + 2xy + 2yx + y2 = 2z2 + 2zy + 2xz + 2xy
⇔ x2 + 2xz + 2xy + 2yz + y2 – 2z2 – 2zy – 2xz – 2xy = 0
⇔ x2 + y2 – 2z2 = 0
⇔ x2 + y2 = 2z2
⇔ z2 = 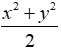
Đáp án cần chọn là: A
Bài 41: Cho các số x, y, z tỉ lệ với các số a, b, c. Khi đó (x2 + 2y2 + 3z2)(a2 + 2b2 + 3c2) bằng
A. ax + 2by + 3cz
B. (2ax + by + 3cz)2
C. (2ax + 3by + cz)2
D. (ax + 2by + 3cz)2
Lời giải
Vì x, y, z tỉ lệ với các số a, b, c nên 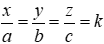
Thay x = ka, y = kb, z = kc vào (x2 + 2y2 + 3z2)(a2 + 2b2 + 3c2) ta được
[(ka)2 + 2(kb)2 + 3(kc)2](a2 + 2b2 + 3c2)
= (k2a2 + 2k2b2 + 3k2c2)(a2 + 2b2 + 3c2)
= k2(a2 + 2b2 + 3c2)(a2 + 2b2 + 3c2)
= k2(a2 + 2b2 + 3c2)2 = [k((a2 + 2b2 + 3c2)]2
= (ka2 + 2kb2 + 3kc2)2
= (ka.a + 2kb.b + 3kc.c)2
= (xa + 2yb + 3zc)2 do x = ka,y = kb, z = kc
Vậy (x2 + 2y2 + 3z2)(a2 + 2b2 + 3c2) = (ax + 2by + 3cz)2
Đáp án cần chọn là: D
Bài 42: Cho B = (m – 1)(m + 6) – (m + 1)(m – 6). Chọn kết luận đúng.
A. B ⁝ 10 với mọi m Є Z
B. B ⁝ 15 với mọi m Є Z
C. B ⁝ 9 với mọi m Є Z
D. B ⁝ 20 với mọi m Є Z
Lời giải
Ta có B = (m – 1)(m + 6) – (m + 1)(m – 6)
= m2 + 6m – m – 6 – (m2 – 6m + m – 6)
= m2 + 5m – 6 – m2 + 6m – m + 6 = 10m
Nhận thấy 10 ⁝ 10 ⇒ 10.m ⁝ 10 nên B ⁝ 10 với mọi giá trị nguyên của m.
Đáp án cần chọn là: A
Bài 43: Cho m số mà mỗi số bằng 3n – 1 và n số mà mỗi số bằng 9 – 3m. Biết tổng tất cả các số đó bằng 5 lần tổng m + n. Khi đó
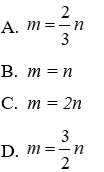
Lời giải
+ Tổng của m số mà mỗi số bằng 3n – 1 là m(3n – 1)
+ Tổng của n số mà mỗi số bằng 9 – 3m là n(9 – 3m)
Tổng tất cả các số trên là m(3n – 1) + n(9 – 3m)
Theo đề bài ta có
m(3n – 1) + n(9 – 3m) = 5(m + n)
⇔ 3mn – m + 9n – 3mn = 5m + 5n
⇔ 6m = 4n ⇔
Vậy
Đáp án cần chọn là: A
Bài 44: Tính tổng các hệ số của lũy thừa bậc ba, lũy thừa bậc hai và lũy thừa bậc nhất trong kết quả của phép nhân (x2 + x + 1)(x3 – 2x + 1)
A. 1
B. -2
C. – 3
D. 3
Lời giải
Ta có (x2 + x + 1)(x3 – 2x + 1)
= x2.x3 + x2.(-2x) + x2.1 + x.x3 + x.(-2x) + x.1 + 1.x3 + 1.(-2x) + 1.1
= x5 – 2x3 + x2 + x4 – 2x2 + x + x3 – 2x + 1
= x5 + x4 – x3 – x2 – x + 1
Hệ số của lũy thừa bậc ba là – 1
Hệ số của lũy thừa bậc hai là – 1
Hệ số của lũy thừa bậc nhất là – 1
Tổng các hệ số này là -1 +(-1) + (-1) = -3
Đáp án cần chọn là: C
Bài 45: Nếu a + b = m và ab = n thì
A. (x + a)(x + b) = x2 + mx + n
B. (x + a)(x + b) = x2 + nx + m
C. (x + a)(x + b) = x2 – mx – n
D. (x + a)(x + b) = x2 – mx + n