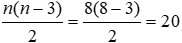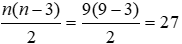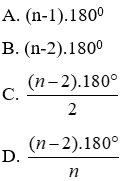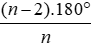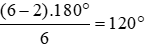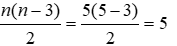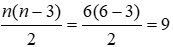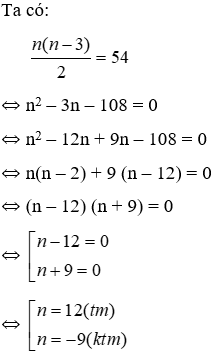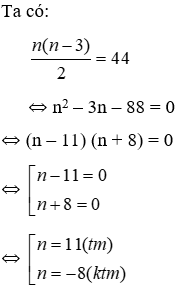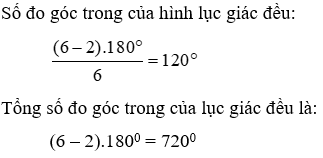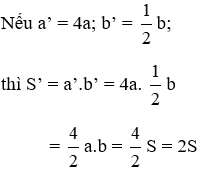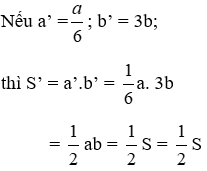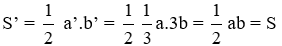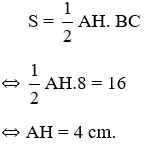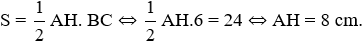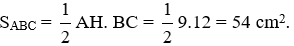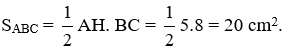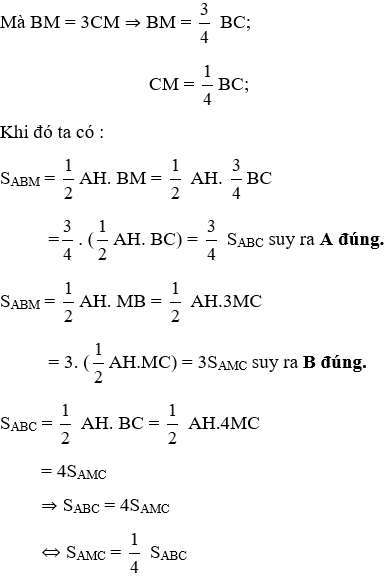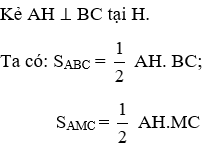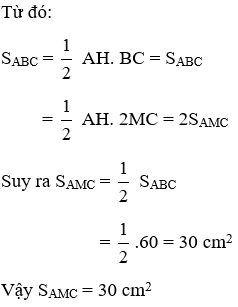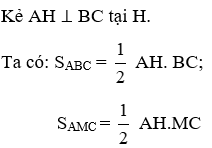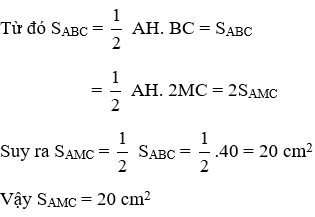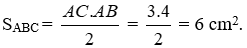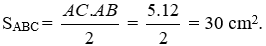Bài tập trắc nghiệm Toán lớp 8 Chương 2 Hình học có đáp án

---

Bài tập trắc nghiệm Toán lớp 8 Chương 2 Hình học có đáp án

Với bộ Bài tập trắc nghiệm Toán lớp 8 Chương 2 Hình học có đáp án, chọn lọc sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 8.

• Trắc nghiệm Đa giác. Đa giác đều
• Trắc nghiệm Diện tích hình chữ nhật
• Trắc nghiệm Diện tích hình thang
• câu trắc nghiệm Chương 2 Hình học 8 có đáp án

Trắc nghiệm Đa giác. Đa giác đều có đáp án

Bài 1: Cho đa giác 8 cạnh, số đường chéo của đa giác đó là:

A. 40

B. 28

C. 20

D. 16

Hiển thị đáp án

Lời giải

Số đường chéo của đa giác lồi n cạnh bằng

Đáp án cần chọn là: C

Bài 2: Cho đa giác 9 cạnh, số đường chéo của đa giác đó là:

A. 36

B. 27

C. 20

D. 18

Hiển thị đáp án

Lời giải

Số đường chéo của đa giác lồi n cạnh bằng

Đáp án cần chọn là: B

Bài 3: Tổng số đo các góc của đa giác đều 7 cạnh là:

A. 900⁰

B. 540⁰

C. 1080⁰

D. 108⁰

Hiển thị đáp án

Lời giải

Tổng các góc của đa giác 7 cạnh bằng (7 – 2).180⁰ = 900⁰

Đáp án cần chọn là: A

Bài 4: Tổng số đo các góc của đa giác đều 9 cạnh là:

A. 900⁰

B. 1026⁰

C. 1080⁰

D. 1260⁰

Hiển thị đáp án

Lời giải

Tổng các góc của đa giác 7 cạnh bằng (9 – 2).180⁰ = 1260⁰

Đáp án cần chọn là: D

Bài 5: Mỗi góc trong của đa giác đều n cạnh là:

Hiển thị đáp án

Lời giải

Mỗi góc của đa giác đều n cạnh bằng

Đáp án cần chọn là: D

Bài 6: Mỗi góc trong của lục giác đều là:

A. 120⁰

B. 150⁰

C. 90⁰

D. 135⁰

Hiển thị đáp án

Lời giải

Mỗi góc của lục giác đều bằng

Đáp án cần chọn là: A

Bài 7: Tổng số đo các góc của hình đa giác n cạnh là 1440⁰ thì số cạnh n là:

A. n = 9

B. n = 10

C. n = 7 

D. n = 8

Hiển thị đáp án

Lời giải

Từ giả thiết ta có (n – 2).180⁰ = 1440⁰ ⇔ n – 2 = 8 ⇔ n = 10

Đáp án cần chọn là: B

Bài 8: Tổng số đo các góc của hình đa giác n cạnh là 1620⁰ thì số cạnh n là:

A. n = 9

B. n = 10

C. n = 11

D. n = 8

Hiển thị đáp án

Lời giải

Từ giả thiết ta có (n – 2).180⁰ = 1620⁰ ⇔ n – 2 = 9 ⇔ n = 11

Đáp án cần chọn là: C

Bài 9: Tổng số đường chéo của ngũ giác lồi là:

A. 7

B. 8

C. 5

D. 10

Hiển thị đáp án

Lời giải

Số các đường chéo của đa giác lồi 5 cạnh bằng

Đáp án cần chọn là: C

 

Bài 10: Tổng số đường chéo của lục giác lồi là:

A. 9

B. 8

C. 11

D. 10

Hiển thị đáp án

Lời giải

Số các đường chéo của đa giác lồi 6 cạnh bằng

Đáp án cần chọn là: A

Bài 10: Một đa giác có số đường chéo là 54 thì có số cạnh là:

A. 9

B. 10

C. 5

D. 12

Hiển thị đáp án

Lời giải

Số cạnh của đa giác là 12

Đáp án cần chọn là: D

Bài 11: Một đa giác có số đường chéo là 44 thì có số cạnh là:

A. 11

B. 10

C. 5

D. 12

Hiển thị đáp án

Lời giải

Số cạnh của đa giác là 12

Số cạnh của đa giác là 11

Đáp án cần chọn là: A

Bài 12: Chọn câu đúng. Cho các hình: Hình chữ nhật, hình thoi, hình vuông, tam giác cân, tam giác đều.

A. 1

B. 2

C. 4

D. 5

Hiển thị đáp án

Lời giải

Hình vuông là tứ giác đều (có bốn cạnh bằng nhau và các góc cùng bằng 90⁰) và tam giác đều là những đa giác đều.

Hình chữ nhật là đa giác không đều vì hình chữ nhật có 4 góc vuông nhưng các cạnh không bằng nhau nên không là đa giác đều.

Hình thoi là đa giác không đều vì các cạnh bằng nhau nhưng các góc không bằng nhau.

Tam giác cân không là đa giác đều vì có ba cạnh không bằng nhau

Đáp án cần chọn là: B

Bài 13: Chọn câu đúng

A. Lục giác có sáu góc bằng nhau là lục giác đều.  

B. Hình thoi là đa giác không đều có các góc bằng nhau.

C. Ngũ giác có năm cạnh bằng nhau được gọi là ngũ giác đều.

D. Hình chữ nhật là đa giác không đều có các góc bằng nhau.

Hiển thị đáp án

Lời giải

Hình chữ nhật là đa giác không đều vì hình chữ nhật có 4 góc vuông nhưng các cạnh không bằng nhau nên không là đa giác đều.

Hình thoi là đa giác không đều vì các cạnh bằng nhau nhưng các góc không bằng nhau.

Đáp án cần chọn là: D

Bài 14: Cho ABCDEF là hình lục giác đều. Hãy chọn câu sai:

A. ABCDEF có một tâm đối xứng

B. Mỗi góc trong của nó là 120⁰.

C. Tổng các góc trong của nó là 720⁰.  

D. Mỗi góc trong của nó là 150⁰.

Hiển thị đáp án

Lời giải

Số cạnh của đa giác là 12

Câu sai là: Mỗi góc trong của nó là 150⁰.

Đáp án cần chọn là: D

Bài 15: Cho ABCDEF là hình ngũ giác đều. Hãy chọn câu sai:

A. ABCDEF có một tâm đối xứng

B. Mỗi góc trong của nó là 108⁰.

C. Tổng các góc trong của nó là 450⁰.  

D. Tổng các góc trong của nó là 540⁰.

Hiển thị đáp án

Lời giải

Số cạnh của đa giác là 12

Câu sai là: Tổng các góc trong của nó là 450⁰.

Đáp án cần chọn là: C

Trắc nghiệm Diện tích hình chữ nhật có đáp án

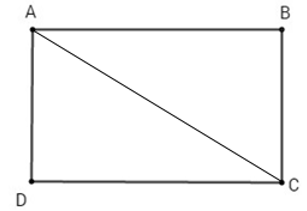
Bài 1: Cho hình chữ nhật ABCD có AC là đường chéo. Chọn câu đúng.

A. S_ABCD = AB

B. S_ABCD = DA. DC

C. S_ABC = AB.BC

D. S_ADC = AD. DC

Hiển thị đáp án

Lời giải

Vì ABCD là hình chữ nhật nên S_ABCD = AD.DC = AB.AD nên A sai, B đúng

Ta có: ΔADC, ΔABC là các tam giác vuông nên S_ADC =  AD.DC; S_ABC =  AB.BC, do đó C, D sai.

Đáp án cần chọn là: B

Bài 2: Hình chữ nhật có chiều dài tăng 4 lần, chiều rộng giảm 2 lần, khi đó diện tích hình chữ nhật

A. Không thay đổi

B. Tăng 2 lần

C. Giảm 2 lần

D. Tăng 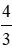lần

Hiển thị đáp án

Lời giải

Theo công thức tính diện tích hình chữ nhật S = a.b thì diện tích hình chữ nhât tỉ lệ thuận với chiều dài và chiều rộng của nó

Do đó diện tích tăng 2 lần so với diện tích đã cho.

Đáp án cần chọn là: B

Bài 3: Hình chữ nhật có chiều dài giảm 6 lần, chiều rộng tăng 3 lần, khi đó diện tích hình chữ nhật

A. Không thay đổi

B. Tăng 2 lần

C. Giảm 2 lần

D. Tăng 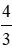lần

Hiển thị đáp án

Lời giải

Theo công thức tính diện tích hình chữ nhật S = a.b thì diện tích hình chữ nhât tỉ lệ thuận với chiều dài và chiều rộng của nó

Do đó diện tích mới giảm 2 lần so với diện tích đã cho.

Đáp án cần chọn là: C

Bài 4: Hình chữ nhật có chiều dài giảm đi 5 lần, chiều rộng tăng lên 5 lần, khi đó diện tích hình chữ nhật

A. Không thay đổi.

B. Tăng 5 lần.

C. Giảm 5 lần.

D. Giảm 3 lần.

Hiển thị đáp án

Lời giải

Gọi a; b lần lượt là chiều dài và chiều rộng của hình chữ nhật ban đầu.

Diện tích hình chữ nhật ban đầu là S = a.b

Nếu giảm chiều dài đi 5 lần thì chiều dài mới là a’ = 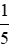a

Nếu tăng chiều rộng lên 5 lần thì chiều rộng mới là b’ = 5b

Lúc này, diện tích hình chữ nhật mới là S’ = a’.b’ = 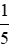a.5b = ab = S

Do đó diện tích hình chữ nhật không thay đổi.

Đáp án cần chọn là: A

Bài 5: Hình tam giác vuông có 1 cạnh góc vuông giảm đi 3 lần và cạnh góc vuông còn lại tăng lên 3 lần, khi đó diện tích hình tam giác vuông mới

A. Không thay đổi

B. Tăng 3 lần

C. Giảm 6 lần

D. Giảm 3 lần

Hiển thị đáp án

Lời giải

Theo công thức tính diện tích tam giác vuông có 2 cạnh góc vuông có độ dài là a, b là S = a.b

Tam giác vuông mới có độ dài hai cạnh góc vuông a’, b’ thì theo đề bài ta có 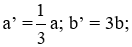khi đó, diện tích

Do đó diện tích hình tam giác mới không thay đổi so với tam giác ban đầu

Đáp án cần chọn là: A

Bài 6: Cho tam giác ABC, biết diện tích tam giác là 16 cm² và cạnh BC = 8 cm. Đường cao tương ứng với cạnh BC là:

A. 5 cm

B. 8 cm

C. 6 cm

D. 4 cm

Hiển thị đáp án

Lời giải

Gọi AH là đường cao ứng với cạnh BC. Theo công thức tính diện tích tam giác ta có

Đáp án cần chọn là: D

Bài 7: Cho tam giác ABC, biết diện tích tam giác là 24 cm² và cạnh BC = 6 cm. Đường cao tương ứng với cạnh BC là:

A. 16 cm

B. 8 cm

C. 6 cm

D. 4 cm

Hiển thị đáp án

Lời giải

Gọi AH là đường cao ứng với cạnh BC. Theo công thức tính diện tích tam giác ta có

Đáp án cần chọn là: B

Bài 8: Cho tam giác ABC, đường cao AH = 9 cm, cạnh BC = 12 cm. Diện tích tam giác là:

A. 108 cm²

B. 72 cm²

C. 54 cm²

D. 216 cm²

Hiển thị đáp án

Lời giải

Từ công thức tính diện tích tam giác ta có:

Đáp án cần chọn là: C

Bài 9: Cho tam giác ABC, đường cao AH = 5 cm, cạnh BC = 8 cm. Diện tích tam giác là:

A. 18 cm²  

B. 15 cm²

C. 40 cm²

D. 20 cm²

Hiển thị đáp án

Lời giải

Từ công thức tính diện tích tam giác ta có:

Đáp án cần chọn là: D

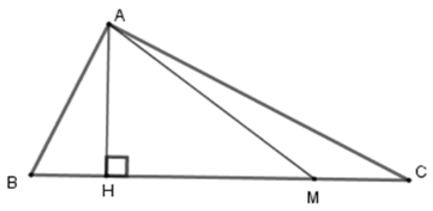
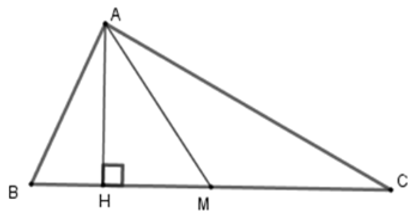
Bài 10: Cho tam giác ABC, lấy M thuộc BC sao cho BM = 3CM. Hãy chọn câu sai:

Hiển thị đáp án

Lời giải

Kẻ AH ⊥ BC tại H.

Suy ra D đúng, C sai.

Đáp án cần chọn là: C

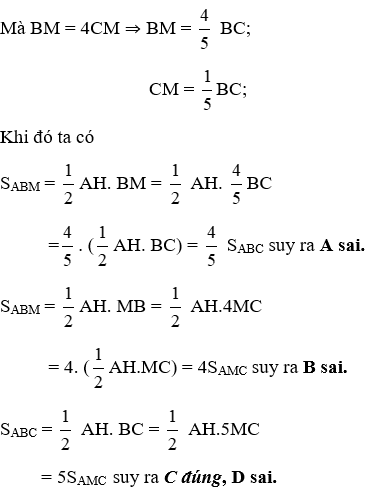
Bài 11: Cho tam giác ABC, lấy M thuộc BC sao cho BM = 4CM. Hãy chọn câu đúng

Hiển thị đáp án

Lời giải

Kẻ AH ⊥ BC tại H.

Đáp án cần chọn là: C

Bài 12: Cho tam giác ABC, AM là đường trung tuyến. Biết diện tích của ΔABC bằng 60 cm². Diện tích của tam giác AMC là:

A. S_AMC = 30 cm²

B. S_ABC = 120 cm²

C. S_AMC = 15 cm²

D. S_AMC = 40 cm²

Hiển thị đáp án

Lời giải

Mà AM là đường trung tuyến nên M là trung điểm của BC ⇒ BC = 2AM

Đáp án cần chọn là: A

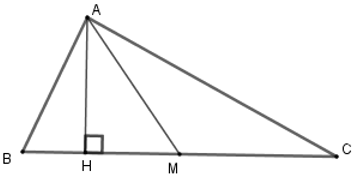
Bài 13: Cho tam giác ABC, AM là đường trung tuyến. Biết diện tích của ΔABC bằng 40 cm². Diện tích của tam giác AMC là:

A. S_AMC = 80 cm²

B. S_ABC = 120 cm²

C. S_AMC = 20 cm²

D. S_AMC = 40 cm²

Hiển thị đáp án

Lời giải

Mà AM là đường trung tuyến nên M là trung điểm của BC ⇒ BC = 2AM

Đáp án cần chọn là: C

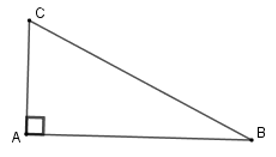
Bài 14: Cho tam giác ABC vuông tại A, biết BC = 5 cm; AC = 3 cm. Diện tích tam giác ABC là:

A. 15 cm²

B. 5 cm²

C. 6 cm²

D. 7, 5 cm²

Hiển thị đáp án

Lời giải

+ Áp dụng định lý Pytago cho tam giác vuông ABC ta có: BC² = AC² + AB² ⇒ AB² = 5² – 3² ⇒ AB² = 16 ⇒ AB = 4 cm

+ Suy ra

Đáp án cần chọn là: C

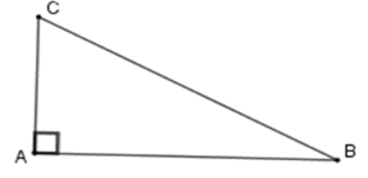
Bài 15: Cho tam giác ABC vuông tại A, biết BC = 13 cm; AC = 5 cm. Diện tích tam giác ABC là:

A. 30 cm²

B. 60 cm²

C. 40 cm²

D. 20 cm²

Hiển thị đáp án

Lời giải

+ Áp dụng định lý Pytago cho tam giác vuông ABC ta có: BC² = AC² + AB² ⇒ AB² = 13² – 5² ⇒ AB² = 144 ⇒ AB = 12 cm

+ Suy ra

Đáp án cần chọn là: A