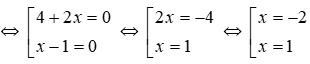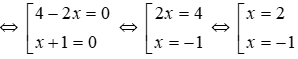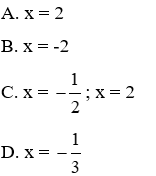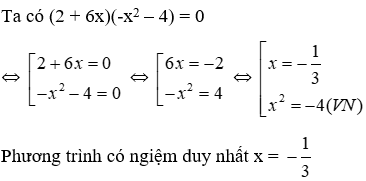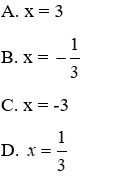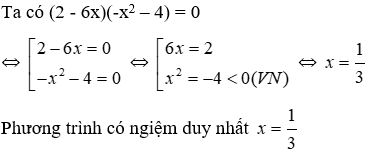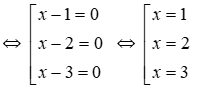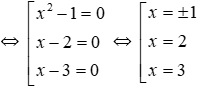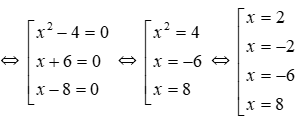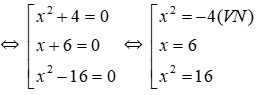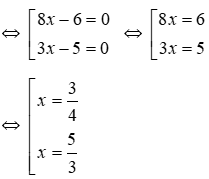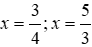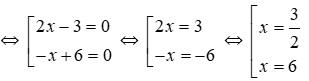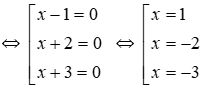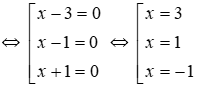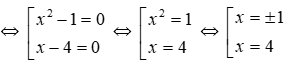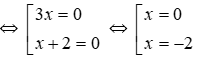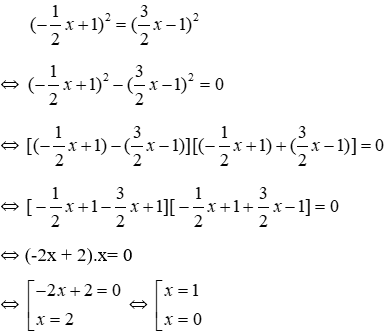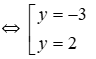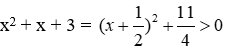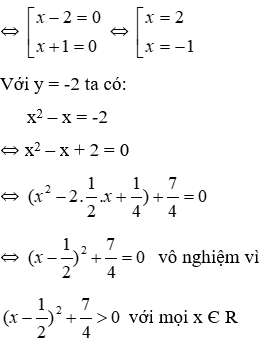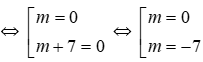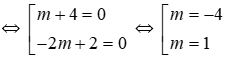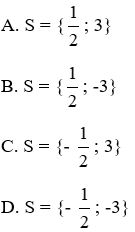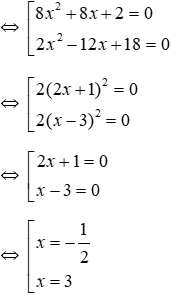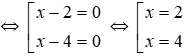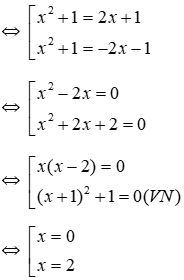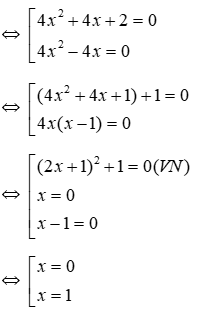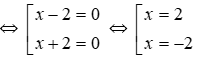Trắc nghiệm Phương trình tích có đáp án - Toán lớp 8
Trắc nghiệm Phương trình tích có đáp án
Với bộ bài tập Trắc nghiệm Phương trình tích Toán lớp 8 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 8.

Bài 1: Phương trình: (4 + 2x)(x – 1) = 0 có nghiệm là:
A. x = 1; x = 2
B. x = -2; x = 1
C. x = -1; x = 2
D. x = 1; x = 2
Lời giải
Ta có (4 + 2x)(x – 1) = 0
Vậy phương trình có hai nghiệm x = -2; x = 1
Đáp án cần chọn là: B
Bài 2: Phương trình: (4 - 2x)(x + 1) = 0 có nghiệm là:
A. x = 1; x = 2
B. x = -2; x = 1
C. x = -1; x = 2
D. x = 1; x = -2
Lời giải
Ta có (4 - 2x)(x + 1) = 0
Vậy phương trình có hai nghiệm x = 2; x = -1
Đáp án cần chọn là: C
Bài 3: Các nghiệm của phương trình (2 + 6x)(-x2 – 4) = 0 là
Lời giải
Đáp án cần chọn là: D
Bài 4: Các nghiệm của phương trình (2 - 6x)(-x2 – 4) = 0 là
Lời giải
Đáp án cần chọn là: D
Bài 5: Phương trình (x – 1)(x – 2)(x – 3) = 0 có số nghiệm là:
A. 1
B. 2
C. 3
D. 4
Lời giải
Ta có (x – 1)(x – 2)(x – 3) = 0
Vậy phương trình có ba nghiệm x = 1; x = 2; x = 3
Đáp án cần chọn là: C
Bài 6: Phương trình (x2 – 1)(x – 2)(x – 3) = 0 có số nghiệm là:
A. 1
B. 2
C. 3
D. 4
Lời giải
Ta có (x2 – 1)(x – 2)(x – 3) = 0
Vậy phương trình có bốn nghiệm x = -1; x = 1, x = 2, x = 3
Đáp án cần chọn là: D
Bài 7: Tổng các nghiệm của phương trình (x2 – 4)(x + 6)(x – 8) = 0 là:
A. 1
B. 2
C. 3
D. 4
Lời giải
Ta có (x2 – 4)(x + 6)(x – 8) = 0
Tổng các nghiệm của phương trình là 2 + (-2) + (-6) + 8 = 2
Đáp án cần chọn là: B
Bài 8: Tổng các nghiệm của phương trình (x2 + 4)(x + 6)(x2 – 16) = 0 là:
A. 16
B. 6
C. -10
D. -6
Lời giải
Ta có (x2 + 4)(x + 6)(x2 – 16) = 0
Tổng các nghiệm của phương trình là: -6 + (-4) + 4 = -6
Đáp án cần chọn là: D
Bài 9: Chọn khẳng định đúng.
A. Phương trình 8x(3x – 5) = 6(3x – 5) có hai nghiệm trái dấu
B. Phương trình 8x(3x – 5) = 6(3x – 5) có hai nghiệm dương
C. Phương trình 8x(3x – 5) = 6(3x – 5) có hai nghiệm cùng âm
D. Phương trình 8x(3x – 5) = 6(3x – 5) có một nghiệm duy nhất
Lời giải
Ta có 8x(3x – 5) = 6(3x – 5)
⇔ 8x(3x – 5) - 6(3x – 5) = 0
⇔ (8x – 6)(3x – 5) = 0
Vậy phương trình đã cho có hai nghiệm cùng dương
Đáp án cần chọn là: B
Bài 10: Cho phương trình 5 – 6(2x – 3) = x(3 – 2x) + 5. Chọn khẳng định đúng.
A. Phương trình có hai nghiệm trái dấu
B. Phương trình có hai nghiệm nguyên
C. Phương trình có hai nghiệm cùng dương
D. Phương trình có một nghiệm duy nhất
Lời giải
Ta có 5 – 6(2x – 3) = x(3 – 2x) + 5
⇔ 5 – 5 = x(3 – 2x) + 6(2x – 3)
⇔ 0 = -x(2x – 3) + 6(2x – 3)
⇔ (2x – 3)(-x + 6) = 0
Vậy phương trình đã cho có hai nghiệm cùng dương x = 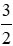
Đáp án cần chọn là: C
Bài 11: Tích các nghiệm của phương trình x3 + 4x2 + x – 6 = 0 là
A. 1
B. 2
C. -6
D. 6
Lời giải
Ta có
x3 + 4x2 + x – 6 = 0
⇔ x3 – x2 + 5x2 – 5x + 6x – 6 = 0
⇔ x2(x – 1) + 5x(x – 1) + 6(x – 1) = 0
⇔ (x – 1)(x2 + 5x + 6) = 0
⇔ (x – 1)(x2 + 2x + 3x + 6) = 0
⇔ (x – 1)[x(x + 2) + 3(x + 2)] = 0
⇔ (x – 1)(x + 2)(x + 3)= 0
Vậy S = {1; -2; -3} nên tích các nghiệm là 1.(-2).(-3) = 6
Đáp án cần chọn là: D
Bài 12: Tích các nghiệm của phương trình x3 – 3x2 – x + 3 = 0 là
A. -3
B. 3
C. -6
D. 6
Lời giải
Ta có x3 – 3x2 – x + 3 = 0
⇔ (x3 – 3x2) – (x – 3) = 0
⇔ x2(x – 3) – (x – 3)= 0
⇔ (x – 3)(x2 – 1) = 0
⇔ (x – 3)(x – 1)(x + 1) = 0
Vậy S = {1; -1; 3} nên tích các nghiệm là 1.(-1).3 = -3
Đáp án cần chọn là: A
Bài 13: Nghiệm lớn nhất của phương trình (x2 – 1)(2x – 1) = (x2 – 1)(x + 3) là:
A. 2
B. 1
C. -1
D. 4
Lời giải
Ta có (x2 – 1)(2x – 1) = (x2 – 1)(x + 3)
⇔ (x2 – 1)(2x – 1) – (x2 – 1)(x + 3) = 0
⇔ (x2 – 1)(2x – 1 – x – 3) = 0
⇔ (x2 – 1)(x – 4) = 0
Vậy tập nghiệm của phương trình S = {-1; 1; 4}
Nghiệm lớn nhất của phương trình là x = 4
Đáp án cần chọn là: D
Bài 14: Số nghiệm của phương trình: (x2 + 9)(x – 1) = (x2 + 9)(x + 3) là
A. 2
B. 1
C. 0
D. 3
Lời giải
Ta có (x2 + 9)(x – 1) = (x2 + 9)(x + 3)
⇔ (x2 + 9)(x – 1) - (x2 + 9)(x + 3) = 0
⇔ (x2 + 9)(x – 1 – x – 3) = 0
⇔ (x2 + 9)(-4) = 0
⇔ x2 + 9 = 0 ⇔ x2 = -9 (vô nghiệm)
Vậy tập nghiệm của phương trình S = Ø hay phương trình không có nghiệm
Đáp án cần chọn là: C
Bài 15: Nghiệm nhỏ nhất của phương trình (2x + 1)2 = (x – 1)2 là
A. 0
B. 2
C. 3
D. -2
Lời giải
Ta có (2x + 1)2 = (x – 1)2
⇔ (2x + 1 + x – 1)(2x + 1 – x + 1) = 0
⇔ 3x(x + 2) = 0
Vậy tập nghiệm của phương trình S = {0; -2}
Nghiệm nhỏ nhất là x = -2
Đáp án cần chọn là: D
Bài 16: Nghiệm nhỏ nhất của phương trình 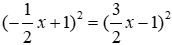
A. 0
B. 2
C. 3
D. -2
Lời giải
Vậy tập nghiệm của phương trình S = {0; 1}
Nghiệm nhỏ nhất x = 0.
Đáp án cần chọn là: A
Bài 17: Tập nghiệm của phương trình (x2 + x)(x2 + x + 1) = 6 là
A. S = {-1; -2}
B. S = {1; 2}
C. S = {1; -2}
D. S = {-1; 2}
Lời giải
Đặt x2 + x = y, ta có
y(y + 1) = 6 ⇔ y2 + y – 6 = 022
⇔ y2 + 2y – 3y – 6 = 0
⇔ y(y + 2) – 3(y + 2) = 0
⇔ (y + 2)(y – 3) = 0
+ Với y = 3, ta có x2 + x + 3 = 0, vô nghiệm vì
+ Với y = 2, ta có x2 + x – 2 = 0 ⇔ x2 + 2x – x – 2 = 0
⇔ x(x + 2) – (x + 2) = 0
⇔ (x + 2)(x – 1) = 0
Vậy S = {1;-2}
Đáp án cần chọn là: C
Bài 18: Tập nghiệm của phương trình (x2 – x – 1)(x2 – x + 1) = 3 là
A. S = {-1; -2}
B. S = {1; 2}
C. S = {1; -2}
D. S = {-1; 2}
Lời giải
Đặt x2 - x = y, ta có
(y – 1)(y + 1)= 3 ⇔ y2 – 1 = 3
⇔ y2 = 3 ⇔ y = ±2
Với y = 2 ta có: x2 – x = 2 ⇔ x2 – x – 2 = 0
⇔ x2 – 2x + x – 2 = 0 ⇔ x(x – 2) + (x – 2) = 0
⇔ (x – 2)(x + 1) = 0
Vậy tập nghiệm của phương trình là S = {-1; 2}
Đáp án cần chọn là: D
Bài 19: Tìm m để phương trình (2m – 5)x – 2m2 + 8 = 42 có nghiệm x = -7
A. m = 0 hoặc m = 7
B. m = 1 hoặc m = -7
C. m = 0 hoặc m = -7
D. m = -7
Lời giải
Thay x = -7 vào phương trình (2m – 5)x – 2m2+ 8 = 42 ta được:
(2m – 5)(-7) – 2m2 + 8 = 43
⇔ -14m + 35 – 2m2 – 35 = 0
⇔ 2m2 + 14m = 0
⇔ 2m(m + 7) = 0
Vậy m = 0 hoặc m = -7 thì phương trình có nghiệm x = -7
Đáp án cần chọn là: C
Bài 20: Tìm m để phương trình (2m – 5)x – 2m2 – 7 = 0 nhận x = -3 làm nghiệm
A. m = 1 hoặc m = 4
B. m = -1 hoặc m = -4
C. m = -1 hoặc m = 4
D. m = 1 hoặc m = -4
Lời giải
Thay x = -3 vào phương trình (2m – 5)x – 2m2 – 7 = 0 ta được
(2m – 5).(-3) – 2m2 – 7 = 0
⇔ -6m + 15 – 2m2 – 7 = 0
⇔ -2m2 – 6m + 8 = 0
⇔ -2m2 – 8m + 2m + 8 = 0
⇔ -2m(m + 4) + 2(m +4) = 0
⇔ (m+ 4)(-2m + 2) = 0
Vậy m = 1 hoặc m = -4 thì phương trình có nghiệm x = -3
Đáp án cần chọn là: D
Bài 21: Tập nghiệm của phương trình (5x2 – 2x + 10)2 = (3x2 +10x – 8)2 là:
Lời giải
(5x2 – 2x + 10)2 = (3x2 +10x – 8)2
⇔ (5x2 – 2x + 10)2 - (3x2 +10x – 8)2 = 0
⇔ (5x2 – 2x + 10 + 3x2 +10x – 8)( 5x2 – 2x + 10 – 3x2 – 10x + 8) = 0
⇔ (8x2 + 8x + 2)(2x2 – 12x + 18) = 0
Vậy phương trình có tập nghiệm: S = {-
Đáp án cần chọn là: C
Bài 22: Số nghiệm của phương trình (5x2 – 2x + 10)3 = (3x2 +10x – 6)3 là:
A. 1
B. 2
C. 3
D. 0
Lời giải
(5x2 – 2x + 10)3 = (3x2 +10x – 6)3
⇔ 5x2 – 2x + 10 = 3x2 +10x – 6
⇔ 5x2 – 3x2 – 2x – 10x + 10 + 6 = 0
⇔ 2x2 – 12x + 16 = 0
⇔ x2 – 6x + 8 = 0
⇔ x2 – 4x – 2x + 8 = 0
⇔ x(x – 4) – 2(x – 4) = 0
⇔ (x – 2)(x – 4) = 0
Vậy phương trình có 2 nghiệm
Đáp án cần chọn là: B
Bài 23: Biết rằng phương trình (x2 – 1)2 = 4x + 1 có nghiệm lớn nhất là x0. Chọn khẳng định đúng
A. x0 = 3
B. x0 < 2
C. x0 > 1
D. x0 < 0
Lời giải
Cộng 4x2 vào hai vế ta được
(x2 – 1)2 = 4x + 1 ⇔ x4 – 2x2 + 1 = 4x + 1
⇔ x4 – 2x2 + 1 + 4x2 = 4x2 + 4x + 1
⇔ (x2 + 1)2 = (2x + 1)2
Vậy S = {0; 2}, nghiệm lớn nhất là x0 = 2 > 1
Đáp án cần chọn là: C
Bài 24: Biết rằng phương trình (4x2 – 1)2 = 8x + 1 có nghiệm lớn nhất là x0. Chọn khẳng định đúng
A. x0 = 3
B. x0 < 2
C. x0 > 1
D. x0 < 0
Lời giải
Cộng 16x2 vào hai vế ta được
(4x2 – 1)2 +16x2 = 16x2 + 8x + 1
⇔ 16x4 – 8x2 + 1 + 16x2 = 16x2 + 8x + 1
⇔ (4x2 + 1)2 = (4x + 1)2
⇔ (4x2 + 1 + 4x + 1)( 4x2 + 1 – 4x – 1) = 0
⇔ (4x2 + 4x + 2)( 4x2 – 4x) = 0
Vậy S = {0; 1}, nghiệm lớn nhất là x0 = 1 < 2
Đáp án cần chọn là: B
Bài 25: Cho phương trình (1): x(x2 – 4x + 5) = 0 và phương trình (2): (x2 – 1)(x2 + 4x + 5) = 0.
Chọn khẳng định đúng
A. Phương trình (1) có một nghiệm, phương trình (2) có hai nghiệm
B. Phương trình (1) có hai nghiệm, phương trình (2) có một nghiệm
C. Hai phương trình đều có hai nghiệm
D. Hai phương trình đều vô nghiệm
Lời giải
Vậy phương trình (1) có một nghiệm duy nhất x = 0.
Vậy phương trình (2) có hai nghiệm x = -1; x = 1
Đáp án cần chọn là: A
Bài 26: Cho phương trình x4 – 8x2 + 16 = 0. Chọn khẳng định đúng
A. Phương trình có hai nghiệm đối nhau
B. Phương trình vô nghiệm
C. Phương trình có một nghiệm duy nhất
D. Phương trình có 4 nghiệm phân biệt
Lời giải
Ta có x4 – 8x2 + 16 = 0
⇔ (x2)2 – 2.4.x2 + 42 = 0 ⇔ (x2 – 4)2
⇔ x2 – 4 = 0 ⇔ (x – 2)(x + 2) = 0
Vậy phương trình có hai nghiệm phân biệt đối nhau
Đáp án cần chọn là: A