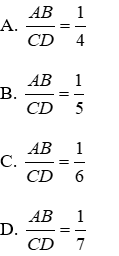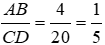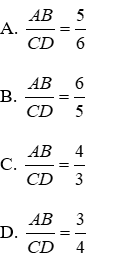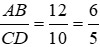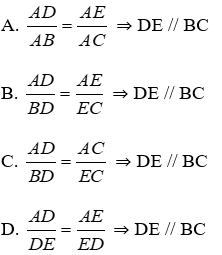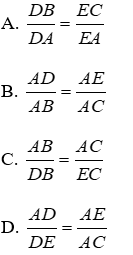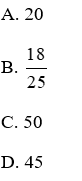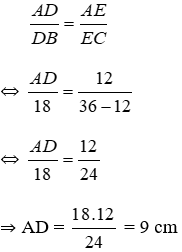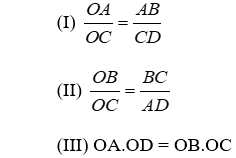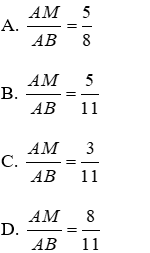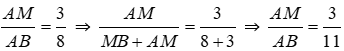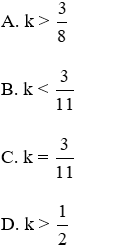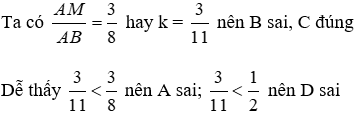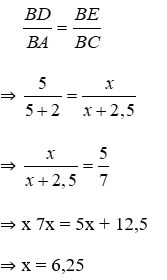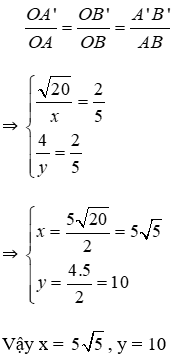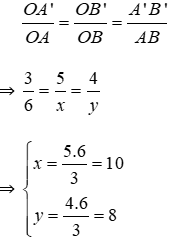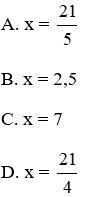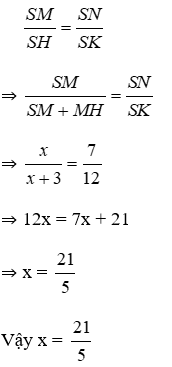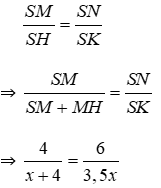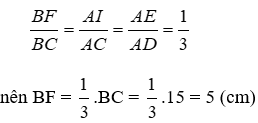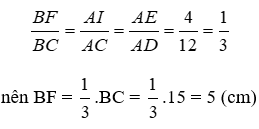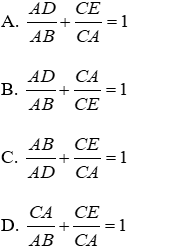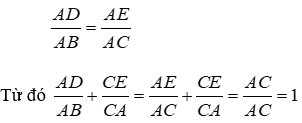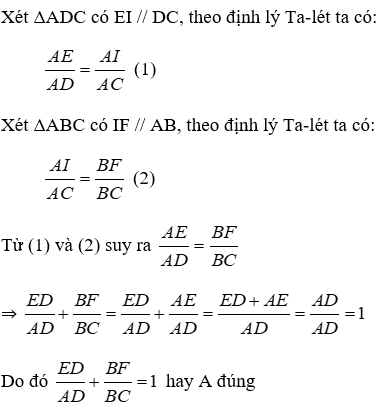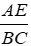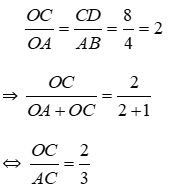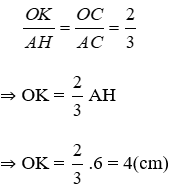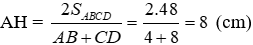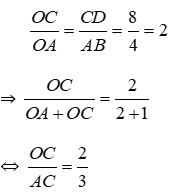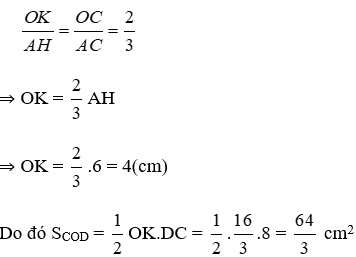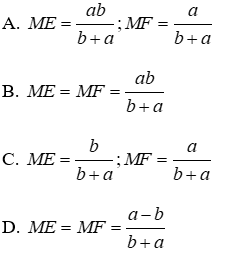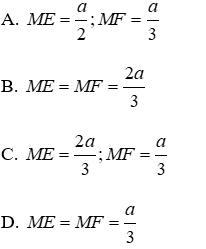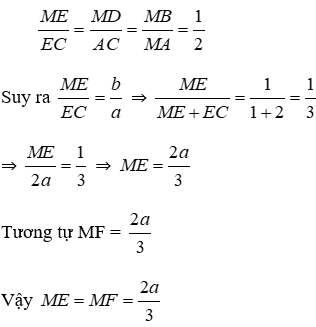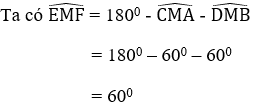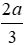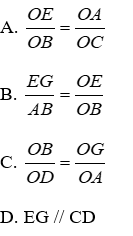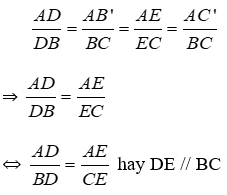Trắc nghiệm Định lí Ta-lét trong tam giác có đáp án - Toán lớp 8
Trắc nghiệm Định lí Ta-lét trong tam giác có đáp án
Với bộ bài tập Trắc nghiệm Định lí Ta-lét trong tam giác Toán lớp 8 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 8.
Bài 1: Viết tỉ số cặp đoạn thẳng có độ dài như sau: AB = 4dm, CD = 20 dm
Lời giải
AB = 4dm, CD = 20 dm ⇒ 
Vậy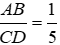 
là tỉ số 2 đoạn thẳng (cùng đơn vị)
Đáp án cần chọn là: B
Bài 2: Viết tỉ số cặp đoạn thẳng có độ dài như sau: AB = 12cm, CD = 10 cm
Lời giải
AB = 12cm, CD = 10 cm ⇒ 
Vậy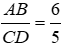 
là tỉ số 2 đoạn thẳng (cùng đơn vị)
Đáp án cần chọn là: B
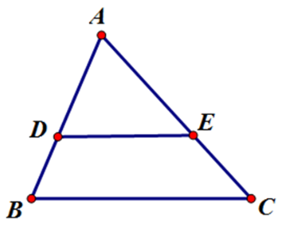
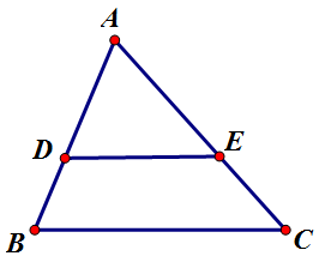
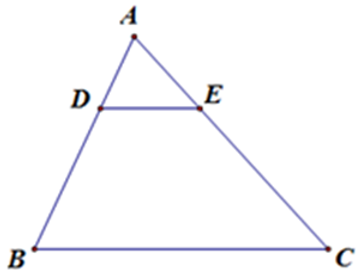
Bài 3: hãy chọn câu sai. Cho hình vẽ với AB < AC:
Lời giải
Theo định lý đảo của định lý Ta-lét. Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Nên D sai.
Đáp án cần chọn là: D
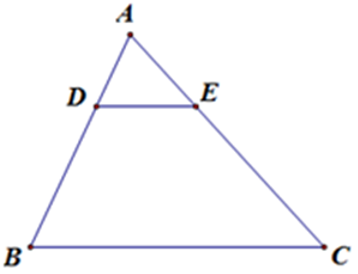
Bài 4: Cho hình vẽ. Điều kiện nào sau đây không suy ra được DE // BC?
Lời giải
Theo định lý đảo của định lý Ta-lét. Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Dễ thấy, từ các điều kiện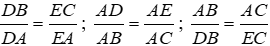 
ta đều suy ra được DE // BC.
Chỉ có D sai.
Đáp án cần chọn là: D
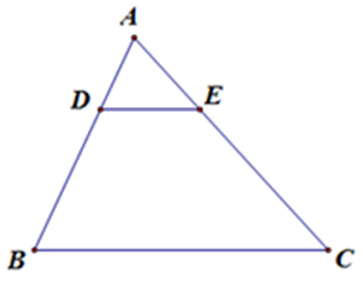
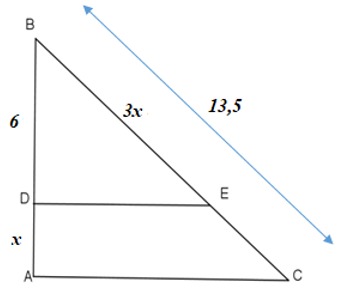
Bài 5: Cho hình vẽ, trong đó DE // BC, AD = 12, DB = 18, CE = 30. Độ dài AC bằng:
Lời giải
Vì DE // BC, theo định lý Ta-lét ta có:
Nên AC = AE + EC = 50 cm
Đáp án cần chọn là: C
Bài 6: Cho hình vẽ, trong đó DE // BC, AE = 12, DB = 18, CA = 36. Độ dài AB bằng:
A. 30
B. 36
C. 25
D. 27
Lời giải
Vì DE // BC, theo định lý Ta-lét ta có:
Nên AB = AD + DB = 9 + 18 = 27 cm
Đáp án cần chọn là: D
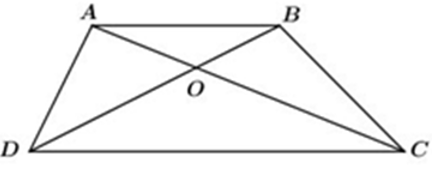
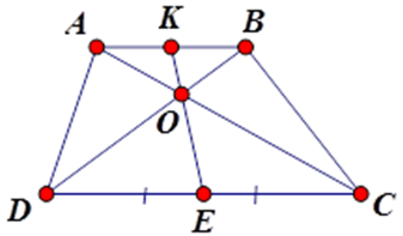
Bài 7: Chọn câu trả lời đúng:
Cho hình thang ABCD (AB // CD), O là giao điểm của AC và BD. Xét các khẳng định sau:
A. Chỉ có (I) đúng
B. Chỉ có (II) đúng
C. Cả (I) và (II) đúng
D. Cả (I) và (II) sai
Lời giải
Đáp án cần chọn là: A
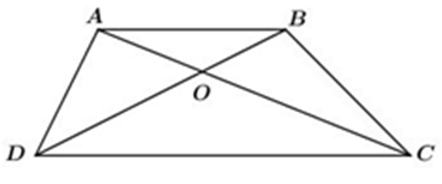
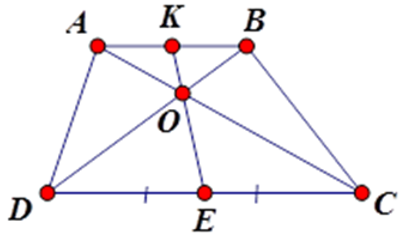
Bài 8: Chọn câu trả lời đúng:
Cho hình thang ABCD (AB // CD), O là giao điểm của AC và BD. Xét các khẳng định sau:
Số khẳng định đúng trong các khẳng định trên là:
A. 1
B. 2
C. 0
D. 3
Lời giải
Vậy có 2 khẳng định đúng.
Đáp án cần chọn là: B
Bài 9: Cho biết M thuộc đoạn thẳng AB thỏa mãn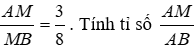 
?
Lời giải
Đáp án cần chọn là: C
Bài 10: Cho biết M thuộc đoạn thẳng AB thỏa mãn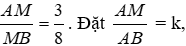 
số k thỏa mãn điều kiện nào dưới đấy?
Lời giải
Đáp án cần chọn là: C
Bài 11: Cho hình vẽ, trong đó AB // CD và DE = EC. Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
A. 1
B. 2
C. 3
D. 4
Lời giải
Đáp án cần chọn là: C
Bài 12: Cho hình vẽ, trong đó AB // CD và DE = EC. Trong các khẳng định sau, có bao nhiêu khẳng định đúng?
A. 1
B. 2
C. 3
D. 4
Lời giải
Theo định lý Ta-lét:
Vậy cả 4 khẳng định đã cho đều đúng.
Đáp án cần chọn là: D
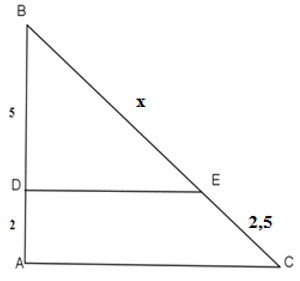
Bài 13: Chọn câu trả lời đúng. Cho hình bên, biết DE // AC, tìm x:
A. x = 6,5
B. x = 6,25
C. x = 5
D. x = 8
Lời giải
Vì DE // AC, áp dụng định lý Talet, ta có:
Đáp án cần chọn là: B
Bài 14: Chọn câu trả lời đúng. Cho hình bên biết ED ⊥ AB, AC ⊥ AB, tìm x:
A. x = 3
B. x = 2,5
C. x = 2
D. x = 4
Lời giải
Ta có: ED ⊥ AB, AC ⊥ AB ⇒ DE // AC (từ vuông góc đến song song), áp dụng định lý Talet, ta có: 
⇔ x2 + 6x – 27 = 0
Vậy x = 3
Đáp án cần chọn là: A
Bài 15: Cho tam giác ABC có AB = 9cm, điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE song song với BC (E Є AC), kẻ EF song song với CD (F Є AB). Tính độ dài AF.
A. 6 cm
B. 5 cm
C. 4 cm
D. 7 cm
Lời giải
Áp dụng định lý Ta-lét:
Đáp án cần chọn là: C
Bài 16: Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB và AC theo thứ tự tại D và E. Qua E kẻ đường thẳng song song với CD, cắt AB ở F. Biết AB = 16, AF = 9, độ dài AD là:
A. 10 cm
B. 15 cm
C. 12 cm
D. 14 cm
Lời giải
Áp dụng định lý Ta-lét:
Vậy 9.16 = AD2 ⇔ AD2 = 144 ⇔ AD = 12
Đáp án cần chọn là: C
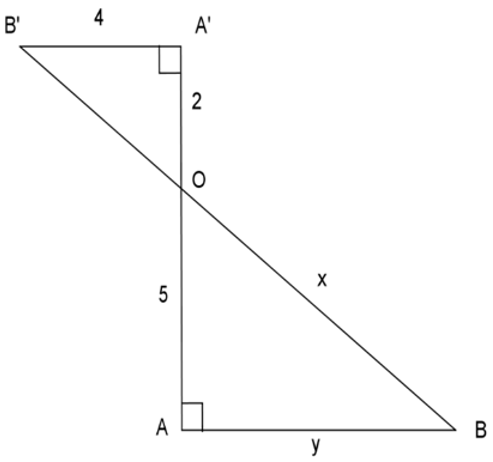
Bài 17: Tính các độ dài x, y trong hình bên:
Lời giải
Áp dụng định lý Py-ta-go cho tam giác vuông OA’B’, ta có: OA’2 + A’B’2 = OB’2
⇔ 22 + 42 = OB’2 ⇔ OB’2 = 20 ⇒ OB’ =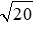 
A’B’ ⊥ AA’, AB ⊥ AA’ ⇒ A’B’// AB
(Theo định lý từ vuông góc đến song song)
Áp dụng định lý Ta-lét, ta có:
Đáp án cần chọn là: D
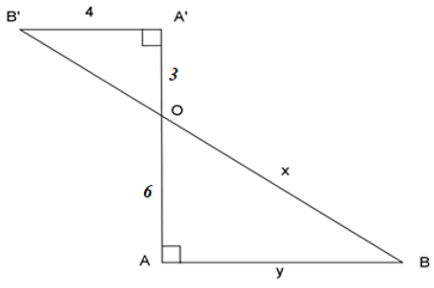
Bài 18: Cho hình vẽ:
Giá trị biểu thức x – y là:
A. 5
B. 3
C. 4
D. 2
Lời giải
Áp dụng định lý Py-ta-go cho tam giác vuông OA’B’, ta có: OA’2 + A’B’2 = OB’2
⇔ 32 + 42 = OB’2 ⇔ OB’2 = 25 ⇒ OB’ = 5
A’B’ ⊥ AA’, AB ⊥ AA’ ⇒ A’B’// AB
(Theo định lý từ vuông góc đến song song)
Áp dụng định lý Ta-lét, ta có:
Hay x – y = 10 – 8 = 2
Đáp án cần chọn là: D
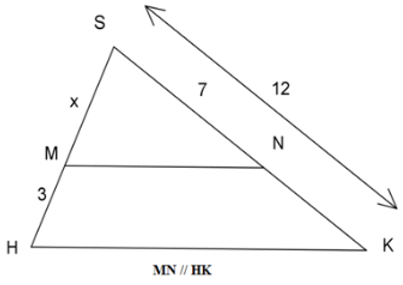
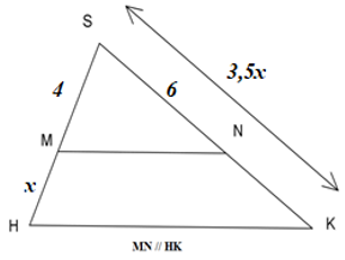
Bài 19: Tìm giá trị của x trên hình vẽ.
Lời giải
Vì MN // HK, áp dụng định lý Ta-lét ta có:
Đáp án cần chọn là: A
Bài 20: Tìm giá trị của x trên hình vẽ.
A. x = 3
B. x = 2,5
B. x = 1
D. x = 3,5
Lời giải
Vì MN // HK, áp dụng định lý Ta-lét ta có:
Vậy x = 3
Đáp án cần chọn là: A
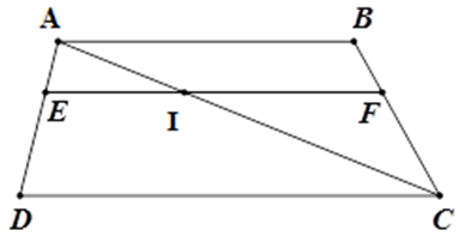
Bài 21: Cho hình thang ABCD (AB // CD) có BC = 15cm. Điểm E thuộc cạnh AD sao cho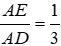 
. Qua E kẻ đường thẳng song song với CD, cắt BC ở F. Tính độ dài BF.
A. 15 cm
B. 5 cm
C. 10 cm
D. 7 cm
Lời giải
Gọi I là giao điểm của AC và EF.
Xét tam giác ACB có IF // AB nên theo định lý Ta-lét ta có:
Đáp án cần chọn là: B
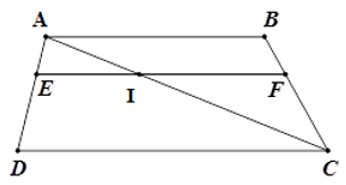
Bài 22: Cho hình thang ABCD (AB // CD) có BC = 15cm, AD = 12 cm. Điểm E thuộc cạnh AD sao cho AE = 4. Qua E kẻ đường thẳng song song với CD, cắt BC ở F. Tính độ dài BF.
A. 10 cm
B. 5 cm
C. 12 cm
D. 7 cm
Lời giải
Gọi I là giao điểm của AC và EF.
Xét tam giác ACB có IF // AB nên theo định lý Ta-lét ta có
Đáp án cần chọn là: B
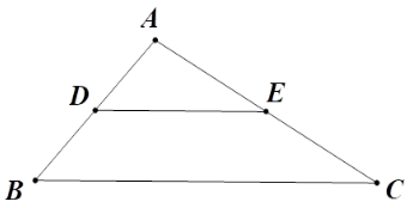
Bài 23: Cho tam giác ABC. Một đường thẳng song song với BC cắt các cạnh AB và AC theo thứ tự ở D và E. Chọn câu đúng.
Lời giải
Vì DE // BC nên theo định lý Ta-lét ta có:
Đáp án cần chọn là: A
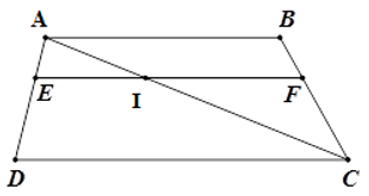
Bài 24: Cho hình thang ABCD (AB // CD). Một đường thẳng song song với AB cắt các cạnh bên AD, BC theo thứ tự ở E, F. Đẳng thức nào sau đây đúng?
Lời giải
Gọi I là giao điểm của AC với EF.
Đáp án cần chọn là: A
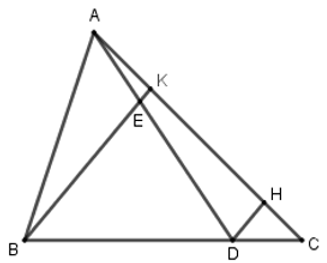
Bài 25: Cho tam giác ABC, đường trung tuyến AD. Gọi K là điểm thuộc đoạn thẳng AD sao cho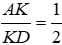 
. Gọi E là giao điểm của Bk và AC. Tính tỉ số 
Lời giải
Kẻ DM // BE ⇒ DM // KE, theo định lý Ta-lét trong tam giác ADM ta có
Đáp án cần chọn là: D
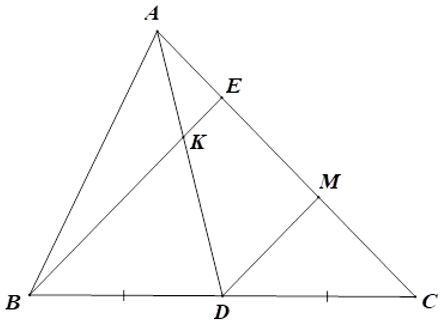
Bài 26: Cho tam giác ABC, điểm D trên cạnh BC sao cho BD = 3/4BC, điểm E trên đoạn AD sao cho AE = 1/3AD. Gọi K là giao điểm của BE với AC. Tỉ số là:
Lời giải
Qua D kẻ đường thẳng song song với BK cắt AC ở H.
Theo định lý Ta-lét:
Đáp án cần chọn là: C
Bài 27: Cho hình thang ABCD (AB // CD) có diện tích 36cm2, AB = 4cm, CD = 8cm. Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác COD.
A. 8cm2
B. 6cm2
C. 16cm2
D. 32cm2
Lời giải
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang: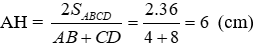 
(cm)
Vì AB // CD (do ABCD là hình thang) nên theo định lý Ta-lét ta có:
Vì AH // OK (cmt) nên theo định lý Ta-lét cho tam giác AHC ta có:
Do đó SCOD = 
OK.DC = .4.8 = 16cm2
Đáp án cần chọn là: C
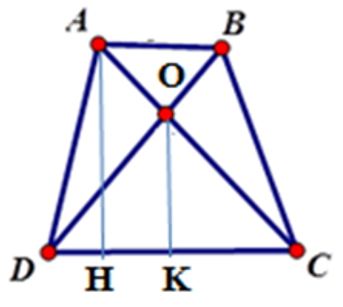
Bài 28: Cho hình thang ABCD (AB // CD) có diện tích 48cm2, AB = 4cm, CD = 8cm. Gọi O là giao điểm của hai đường chéo. Tính diện tích tam giác COD.
Lời giải
Kẻ AH ⊥ DC; OK ⊥ DC tại H, K suy ra AH // OK
Chiều cao của hình thang: 
Vì AB // CD (do ABCD là hình thang) nên theo định lý Ta-lét ta có
Vì AH // OK (cmt) nên theo định lý Ta-lét cho tam giác AHC ta có:
Đáp án cần chọn là: A
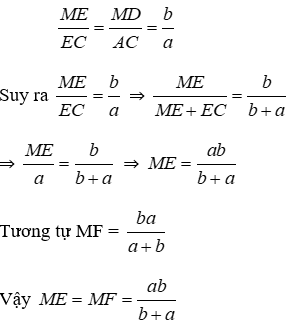
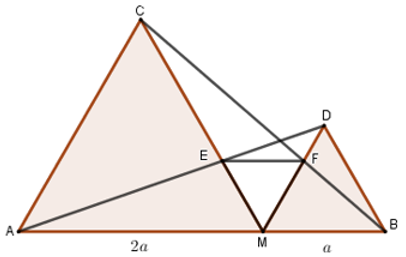
Bài 29: Cho điểm M thuộc đoạn thẳng AB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM.
1. Đặt MA = a, MB = b. Tính ME, MF theo a và b.
Lời giải
Vì các tam giác AMC và BMD đều nên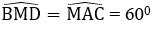 
(vì hai góc ở vị trí đồng vị) ⇒ MD // AC
Vì MD // AC nên theo hệ quả định lý Talet cho hai tam giác DEM và AEC ta có
Đáp án cần chọn là: B
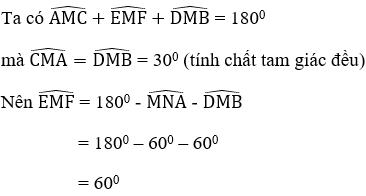
2. Tam giác MEF là tam giác gì? Chọn đáp án đúng nhất?
A. Tam giác MEF đều
B. Tam giác MEF cân tại M
C. Tam giác MEF cân tại N
D. Cả A, B, C đều sai
Lời giải
Từ câu trước ta có ME = MF ⇒ ΔEMF cân tại M
Từ đó MEF là tam giác cân có một góc bằng 600 nên nó là tam giác đều
Đáp án cần chọn là: A
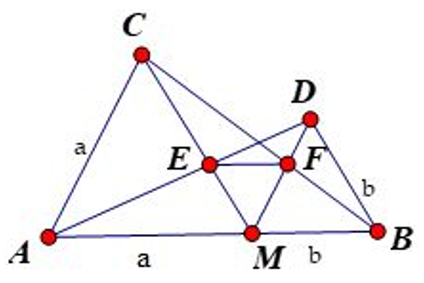
Bài 30: Cho điểm M thuộc đoạn thẳng AB sao cho MA = 2MB. Vẽ về một phía của AB các tam giác đều AMC và MBD. Gọi E là giao điểm của AD và MC, F là giao điểm của BC và DM.
1. Đặt MB = a. Tính ME, MF theo a.
Lời giải
Đặt MB = a ⇒ MA = 2a
Vì các tam giác AMC và BMD đều nên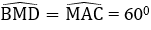 
(hai góc ở vị trí đồng vị) ⇒ MD // AC
Vì MD // AC nên theo hệ quả định lý Talet cho hai tam giác DEM và AEC ta có
Đáp án cần chọn là: B
2. Chọn khẳng định đúng nhất.
Lời giải
Từ câu 1) ta có ME = MF ⇒ ΔEMF cân tại M
Từ đó MEF là tam giác cân có một góc bằng 600 nên nó là tam giác đều
Vậy EF = ME = MF = 
Đáp án cần chọn là: A
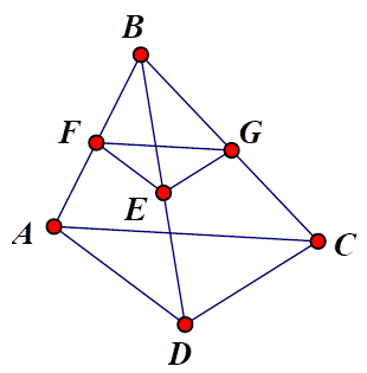
Bài 31: Cho tứ giác ABCD, lấy bất kỳ E Є BD. Qua E vẽ EF song song với AD (F thuộc AB), vẽ EG song song với DC (G thuộc BC). Chọn khẳng định sai.
Lời giải
Áp dụng định lý Ta-lét trong ΔABD với EF // AD, ta có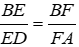 
(1)
Áp dụng định lý Ta-lét trong ΔBDC với EG // DC, ta có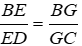 
(2)
Từ (1) và (2) suy ra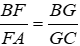 
, do đó FG // AC (định lý Ta-lét đảo)
Vậy A, B, C đúng, D sai
Đáp án cần chọn là: D
Bài 32: Cho tứ giác ABCD có O là giao điểm hai đường chéo. Đường thẳng qua A và song song với BC cắt BD ở E. Đường thẳng qua B song song với AD cắt AC ở G. Chọn kết luận sai?
Lời giải
Theo định lý Ta-lét:
Vậy B sai
Đáp án cần chọn là: B
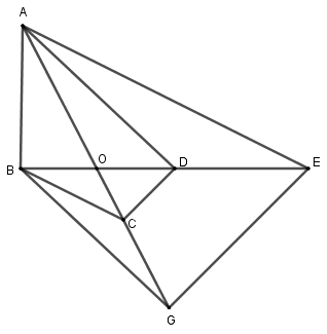
Bài 33: Cho tam giác ABC có AM là đường trung tuyến, N là điểm trên đoạn thẳng AM. Gọi D là giao điểm của CN và AB, E là giao điểm của BN và AC. Chọn khẳng định đúng nhất.
A. DE// BC
B.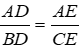 
C. Cả A, B đều đúng
D. Cả A, B đều sai
Lời giải
Kẻ đường thẳng đi qua A song song với BC lần lượt cắt CD và BE kéo dài tại B’ và C’.
Vì M là trung điểm BC nên BM = MC.
Từ (*), (**) và (***) ta có: ⇒
Đáp án cần chọn là: C
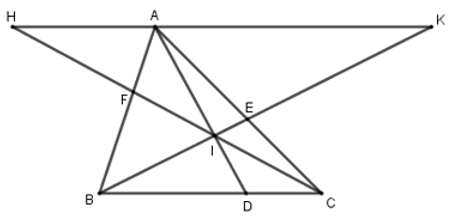
Bài 34: Cho tam giác ABC, điểm I nằm trong tam giác. Các tia AI, BI, CI cắt các cạnh BC, AC, AB theo thứ tự ở D, E, F. Tổng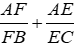 
bằng tỉ số nào dưới đây?
Lời giải
Qua A kẻ đường thẳng song song với BC, cắt CF, BE lần lượt tại H, K
Đáp án cần chọn là: B
