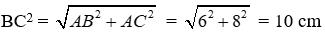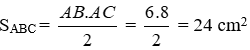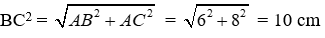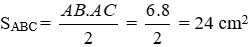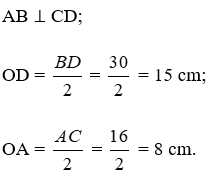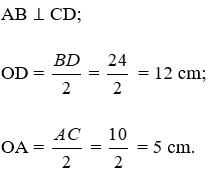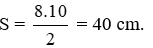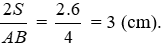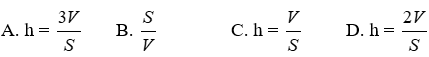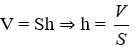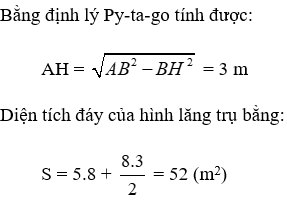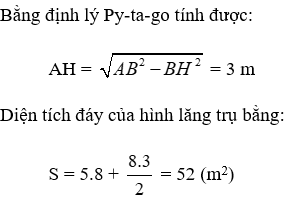Trắc nghiệm Hình lăng trụ đứng có đáp án - Toán lớp 8
Trắc nghiệm Hình lăng trụ đứng có đáp án
Với bộ bài tập Trắc nghiệm Hình lăng trụ đứng Toán lớp 8 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 8.

Bài 1: Các mặt bên của hình lăng trụ đứng là:
A. Các hình bình hành
B. Các hình thang cân
C. Các hình chữ nhật
D. Các hình vuông
Lời giải
Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.
Đáp án cần chọn là: C
Bài 2: Chọn câu đúng.
A. Các mặt bên của hình lăng trụ đứng là các hình chữ nhật
B. Các mặt bên của hình lăng trụ đứng là các hình thang cân
C. Các mặt đáy của hình lăng trụ đứng là các hình chữ nhật
D. Các mặt đáy của hình lăng trụ đứng là các hình tam giác
Lời giải
Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.
Đáp án cần chọn là: A
Bài 3: Các cạnh bên của hình lăng trụ đứng
A. Song song với nhau
B. Bằng nhau
C. Vuông góc với hai đáy
D. Có cả ba tính chất trên
Lời giải
Hình lăng trụ đứng có các mặt bên là những hình chữ nhật, các cạnh bên vuông góc với đáy nên chúng song song và bằng nhau
Đáp án cần chọn là: D
Bài 4: Câu nào không đúng về các cạnh bên của hình lăng trụ đứng
A. Song song với nhau
B. Bằng nhau
C. Vuông góc với hai đáy
D. Vuông góc với nhau
Lời giải
Hình lăng trụ đứng có các mặt bên là những hình chữ nhật, các cạnh bên vuông góc với đáy nên chúng song song và bằng nhau
Chỉ có đáp án D sai.
Đáp án cần chọn là: D
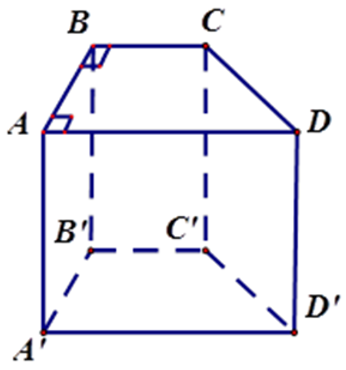
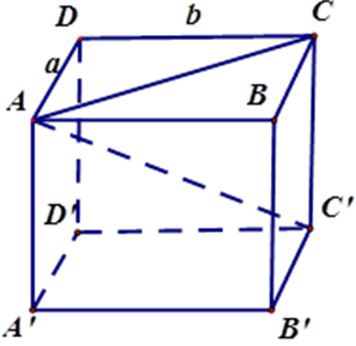
Bài 5: Cho hình lăng trụ đứng ABCD. A'B'C'D' có đáy ABCD là hình thang vuông (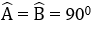
Có bao nhiêu cạnh song song với mặt phẳng (BCC'B')?
A. 1
B. 2
C. 4
D. 5
Lời giải
Vì AA'//BB'//DD' và A'D'//AD/BC nên các đường thẳng AA', DD', AD, A'D' song song với mp (BCC'B')
Đáp án cần chọn là: C
Bài 6: Cho hình lăng trụ đứng ABCD. A'B'C'D' có đáy ABCD là hình thang vuông (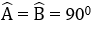
Có bao nhiêu cạnh song song với mặt phẳng (ABB'A')?
A. 1
B. 2
C. 4
D. 5
Lời giải
Vì CC'//BB', DD'//AA'nên các đường thẳn DD', CC' song song với mp (ABB'A')
Đáp án cần chọn là: B
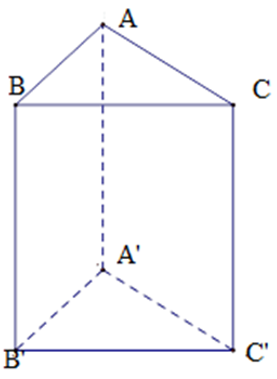
Bài 6: Cho hình lăng trụ đứng ABC. A'B'C' có AB = 5 cm, AC = 12 cm, BC = 13 cm. Có bao nhiêu mặt phẳng vuông góc với mặt phẳng (ABB'A')?
A. 1
B. 2
C. 4
D. 3
Lời giải
Tam giác ABC có:
AB2 + AC2 = 52 + 122 = 132 = BC2 nên ΔABC vuông tại A (định lý Pytago đảo) nên AC ⊥ AB. Do đó A'C' ⊥ A'B'.
Vì AC vuông góc với hai đường thẳng cắt nhau AB và AA' nên AC ⊥ mp (ABB'A') do đó mp (A'B'C') ⊥ mp (ABB'A').
Vậy có ba mặt phẳng vuông góc với mặt phẳng (ABB'A') là mp (ABC), mp (A'B'C'), mp (ACC'A').
Đáp án cần chọn là: D
Bài 7: Cho hình lăng trụ đứng ABC. A'B'C' có AB = 5 cm, AC = 12 cm, BC = 13 cm. Mặt phẳng nào dưới đây không vuông góc với mặt phẳng (ABB'A')?
A. (BCC'B’)
B. (ABC)
C. (A'B'C')
D. (ACC'A')
Lời giải
Tam giác ABC có:
AB2 + AC2 = 52 + 122 = 132 = BC2 nên ΔABC vuông tại A (định lý Pytago đảo) nên AC ⊥ AB. Do đó A'C' ⊥ A'B'.
Vì AC vuông góc với hai đường thẳng cắt nhau AB và AA' nên AC ⊥ mp (ABB'A') do đó mp (A'B'C') ⊥ mp (ABB'A').
Vậy có ba mặt phẳng vuông góc với mặt phẳng (ABB'A') là mp (ABC), mp (A'B'C'), mp (ACC'A').
Đáp án cần chọn là: A
Bài 8: Cho hình lăng trụ đứng ABC. A'B'C' (hình vẽ) có 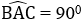
A. 258 cm2
B. 360 cm2
C. 456 cm2
D. 408 cm2
Lời giải
Áp dụng định lý Pytago cho tam giác ABC ta được:
Ta có chu vi đáy:
PABC = AB + AC + BC = 6 + 8 +10 = 24 cm
Diện tích đáy:
Diện tích xung quanh của lăng trụ đứng:
Sxq = 24.15 = 360 cm2.
Diện tích toàn phần Stp = 360 + 2.24 = 408 cm2.
Đáp án cần chọn là: D
Bài 9: Cho hình lăng trụ đứng ABC. A'B'C' có đáy tam giác ABC vuông tại A, AB = 6 cm, AC = 8 cm, AA' = 12 cm. Diện tích toàn phần của hình lăng trụ đó bằng
A. 288 cm2
B. 360 cm2
C. 456 cm2
D. 336 cm2
Lời giải
Áp dụng định lý Pytago cho tam giác ABC ta được
Ta có chu vi đáy
PABC = AB + AC + BC = 6 + 8 +10 = 24 cm
Diện tích đáy:
Diện tích xung quanh của lăng trụ đứng
Sxq = 24.12 = 288 cm2.
Diện tích toàn phần Stp = 360 + 2.24 = 336 cm2.
Đáp án cần chọn là: D
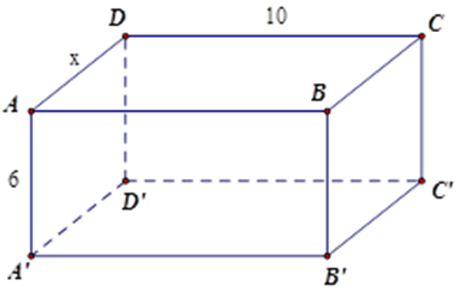
Bài 10: Một hình hộp chữ nhật có diện tích xung quang bằng tổng diện tích hai đáy, chiều cao bằng 6 cm. Một kích thước của đáy bằng 10 cm, tính kích thước còn lại.
A. 15 cm
B. 20 cm
C. 25 cm
D. 10 cm
Lời giải
Đặt AD = x.
Diện tích xung quang bằng:
2 (10 + x).6 (cm2)
Tổng diện tích hai đáy bằng 2.10x (cm2)
Ta có
2 (10 + x).6 = 2.10x ⇔ 60 +6x = 10x ⇔ x = 15
Kích thước còn lại của đáy bằng 15 cm.
Đáp án cần chọn là: A
Bài 11: Một hình hộp chữ nhật có kích thước của đáy là 10 cm và 15 cm. Biết diện tích xug quang bằng tổng diện tích hai đáy. Độ dài chiều cao là:
A. 12 cm
B. 6 cm
C. 8 cm
D. 10 cm
Lời giải
Đặt AA' = x.
Diện tích xung quang bằng:
2 (10 + 15).x = 50x (cm2)
Tổng diện tích hai đáy bằng 2.10.15 = 300 (cm2)
Ta có 50x = 300 ⇔ x = 6
Vậy chiều cao bằng 6 cm.
Đáp án cần chọn là: B
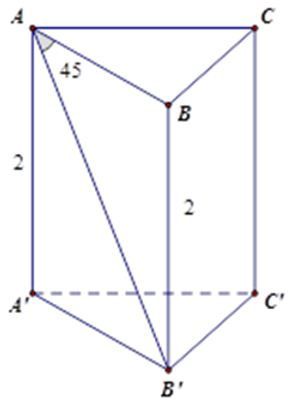
Bài 12: Cho hình lăng trụ tam giác đều ABC. A'B'C' có chiều cao bằng 2 cm, 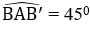
A. 15 cm2
B. 6 cm2
C. 12 cm2
D. 16 cm2
Lời giải
Tam giác vuông ABB' có 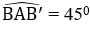
Vì tam giác ABC đều nên chu vi bằng 3AB = 3.2 = 6 cm
Diện tích xung quanh bằng 6.2 = 12 (cm2)
Đáp án cần chọn là: C
Bài 13: Cho hình lăng trụ tam giác đều ABC. A'B'C' có chiều cao bằng 2 cm, 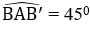
A. 15 cm2
B. 6 cm2
C. 12 cm2
D. 16 cm2
Lời giải
Tam giác vuông ABB' có 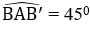
Vì tam giác ABC đều nên chu vi bằng 3AB = 3.2 = 6 cm
Diện tích xung quanh bằng 6.2 = 12 (cm2)
Đáp án cần chọn là: C
Bài 14: Một hình hộp chữ nhật có diện tích xung quanh bằng 120 cm2, chiều cao bằng 6cm. Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất.
A. 8 cm
B. 7 cm
C. 6 cm
D. 5 cm
Lời giải
Gọi a và b là các kích thước của đáy.
Ta có V = 6ab nên V lớn nhât ⇔ ab lớn nhất
Sxq = 120 nên 2 (a+b).6 = 120 hay a + b = 10
Ta có:
ab = a (10 – a) = -a2 +10a = -(a – 5)2 + 25 ≤ 25
Suy ra V = 6ab ≤ 6.25 = 150.
Thể tích lớn nhất bằng 150 cm3 khi a = b = 5, tức là các cạnh đáy bằng 5 cm.
Đáp án cần chọn là: D
Bài 15: Một hình hộp chữ nhật có diện tích xung quanh bằng 100 cm2, chiều cao bằng 5cm. Tìm các kích thước của đáy để hình hộp chữ nhật có thể tích lớn nhất.
A. 8 cm
B. 7 cm
C. 6 cm
D. 5 cm
Lời giải
Gọi a và b là các kích thước của đáy.
Ta có V = 5ab nên V lớn nhât ⇔ ab lớn nhất
Sxq = 100 nên 2 (a+b).5 = 120 hay a + b = 10
Ta có:
ab = a (10 – a) = -a2 +10a = -(a – 5)2 + 25 ≤ 25
Suy ra V = 5ab ≤ 5.25 = 125.
Thể tích lớn nhất bằng 125 cm3 khi a = b = 5, tức là các cạnh đáy bằng 5 cm.
Đáp án cần chọn là: D
Bài 16: Một hình lăng trụ đứng có đáy là hình thoi với các đường chéo của đáy bằng 24 cm và 10 cm. Diện tích toàn phần của hình lăng trụ bằng 1840 cm2. Tính chiều cao của hình lăng trụ.
A. 15 cm
B. 20 cm
C. 30 cm
D. 25 cm
Lời giải
Vì đáy ABCD là hình thoi nên diện tích đáy bằng 16.30:2 = 240 (cm2)
Từ đó diện tích xung quanh
Sxq = 1840 – 240.2 = 1360 (cm2)
Vì ABCD là hình thoi nên:
Nên độ dài cạnh đáy bằng 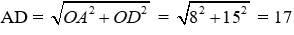
Chu vi đáy bằng 17.4 = 68 (cm)
Chiều cao hình lăng trụ bằng
1360 : 68 = 20 (cm)
Đáp án cần chọn là: B
Bài 17: Một hình lăng trụ đứng có đáy là hình thoi với các đường chéo của đáy bằng 16 cm và 30 cm. Diện tích toàn phần của hình lăng trụ bằng 1840 cm2. Tính chiều cao của hình lăng trụ.
A. 15 cm
B. 20 cm
C. 30 cm
D. 25 cm
Lời giải
Vì đáy ABCD là hình thoi nên diện tích đáy bằng 24.10:2 = 120 (cm2)
Từ đó diện tích xung quanh
Sxq = 1020 – 120.2 = 780 (cm2)
Vì ABCD là hình thoi nên:
Nên độ dài cạnh đáy bằng 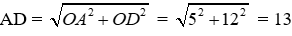
Chu vi đáy bằng 13.4 = 52 (cm)
Chiều cao hình lăng trụ bằng
780 : 52 = 15 (cm)
Đáp án cần chọn là: A
Bài 18: Một hình hộp chữ nhật có đường chéo bằng 3 dm, chiều ao 2 dm, diện tích xung quanh bằng 12 dm2. Tính thể tích của hình hộp chữ nhật.
A. 8 (dm3)
B. 2 (dm3)
C. 4 (dm3)
D. 12 (dm3)
Lời giải
Hình hộp chữ nhật ABCD. A'B'C'D' có AC' = 3dm; CC' = 2dm.
Xét tam giác ACC' vuông tại C, theo định lý Pytago ta có AC2 = C'A2 – C'C2 = 32 – 22 = 5
Vì diện tích xung quang là 12 dm2 nên chu vi đáy bằng 12 : 2 = 6 (dm)
Đặt AD = a, DC = b. Vì chu vi đáy là 6 dm ⇒ 2 (a + b) = 6 ⇔ a + b = 3 (1) và a2 + b2 = AC2 = 5 (2) (định lý Pytago cho tam giác vuông ADC)
Từ đó (1) và (2) suy ra a2 + (3 – a)2 = 5
Rút gọn được a2 – 3a + 2 = 0 hay (a – 1)(a – 2) = 0
Giả sử a ≥ b thì ta tìm được a = 2 suy ra b = 1.
Thể tích của hình hộp chữ nhật bằng 2.1.2 = 4 (dm3).
Đáp án cần chọn là: C
Bài 19: Một hình hộp chữ nhật có đường chéo bằng 3 dm, chiều ao 2 dm, diện tích xung quanh bằng 12 dm2. Diện tích toàn phần của hình hộp chữ nhật là:
A. 8 (dm3)
B. 4 (dm3)
C. 16 (dm3)
D. 12 (dm3)
Lời giải
Hình hộp chữ nhật ABCD. A'B'C'D' có AC' = 3dm; CC' = 2dm.
Xét tam giác ACC' vuông tại C, theo định lý Pytago ta có AC2 = C'A2 – C'C2 = 32 – 22 = 5
Vì diện tích xung quang là 12 dm2 nên chu vi đáy bằng 12 : 2 = 6 (dm)
Đặt AD = a, DC = b. Vì chu vi đáy là 6 dm ⇒ 2 (a + b) = 6 ⇔ a + b = 3 (1) và a2 + b2 = AC2 = 5 (2) (định lý Pytago cho tam giác vuông ADC)
Từ đó (1) và (2) suy ra a2 + (3 – a)2 = 5
Rút gọn được a2 – 3a + 2 = 0 hay (a – 1)(a – 2) = 0
Giả sử a ≥ b thì ta tìm được a = 2 suy ra b = 1.
Diện tích toàn phần của hình hộp chữ nhật bằng: 12 + 2.1.2 = 16 (dm3)
Đáp án cần chọn là: C
Bài 20: Tính thể tích của hình lăng trụ đứng có chiều cao 20 cm, đáy là một tam giác vuông có các cạnh góc vuông bằng 8 cm và 10 cm:
A. 800 cm3
B. 400 cm3
C. 600 cm3
D. 500 cm3
Lời giải
Vì đáy là tam giác vuông nên diện tích đáy
Thể tích lăng trụ đứng là V = S.h = 40.20 = 800 cm3
Đáp án cần chọn là: A
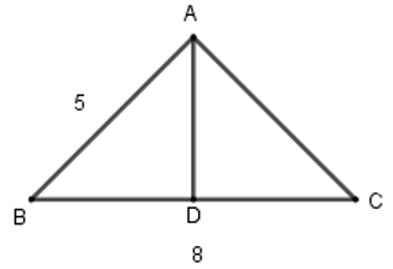
Bài 21: Tính thể tích của hình lăng trụ đứng có chiều cao 20 cm, đáy là một tam giác cân có các cạnh bên bằng 5 cm và cạnh đáy bằng 8 cm.
A. 320 cm3
B. 200 cm3
C. 120 cm3
D. 240 cm3
Lời giải
Gọi D là trung điểm của BC thì AD là trung tuyến cũng là đường cao trong tam giác
Tam giác ADC vuông tại D nên AD2 + DC2 = AC2 ⇔AD2 + 42 = 52 ⇔ AD = 9 ⇔ AD = 3
Diện tích đáy:
Thể tích lăng trụ đứng là: V = S.h = 12.20 = 240 cm3
Đáp án cần chọn là: D
Bài 22: Cho lăng trụ đứng có kích thước như hình vẽ.
Số nào trong các số sau đây là thể tích của hình lăng trụ đứng đó?
A. 20 cm3
B. 36 cm3
C. 26 cm3
D. 9 cm3
Lời giải
Hình lăng trụ đứng đã cho có đáy là một tam giác vuông.
Áp dụng định lý Pytago cho tam giác vuông ABC, ta có:
AB2 + AC2 = BC2 ⇔ 42 + AC2 = 52 ⇔ AC2 = 52 – 42 = 9 ⇒ AC = 3 cm.
Vậy diện tích đáy của hình lăng trụ đứng là:
Vậy thể tích của hình lăng trụ đứng là:
V = S.h = S.BE = 6.6 = 36 cm2
Đáp án cần chọn là: B
Bài 23: Cho lăng trụ đứng có kích thước như hình vẽ.
Biết thể tích hình lăng trụ bằng 36 cm3, độ dài cạnh BC là:
A. 5 cm
B. 3 cm
C. 6 cm
D. 4 cm
Lời giải
Diện tích tam giác ABC là: S = 36 : 6 = 6 (cm2).
Độ dài cạnh AC là:
Tam giác ABC vuông tại A nên
BC2 = AB2 + AC2 = 42 + 32 = 25 ⇒ BC = 5 (cm)
Đáp án cần chọn là: A
Bài 24: Cho một hình lăng trụ đứng có diện tích đáy là S, chiều cao là h. Hỏi công thức tính thể tích hình lăn trụ đứng là gì?
A. S.h
B. 
C. 2S.h
D. 3S.h
Lời giải
Công thức tính thể tích hình lăng trụ đứng là: V = S.h
Đáp án cần chọn là: A
Bài 25: Cho một hình lăng trụ đứng có thể tích V, diện tích đáy là S, chiều cao hình lăng trụ được tính theo công thức:
Lời giải
Ta có:
Đáp án cần chọn là: C
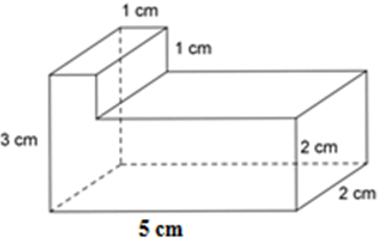
Bài 26: Tính thể tích của hình lăng trụ đứng sau:
A. 16 cm3
B. 20 cm3
C. 26 cm3
D. 22 cm3
Lời giải
Hình lăng trụ đứng đã cho được tạo thành từ 2 hình hộp chữ nhật. Hình hộp chữ nhật thứ nhất có kích thước là 3 cm, 1 cm, 2 cm; hình hộp chữ nhật thứ hai có kích thước là 2 cm; 4 cm; 2m.
Thể tích hình hộp chữ nhật thứ nhất là: V1 = 3.1.2 = 6 cm3
Thể tích hình hộp chữ nhật thứ hai là: V2 = 2.4.2 = 16 cm3
Thể tích hình lăng trụ đứng là: V = V1 + V2 = 6 +16 = 22 cm3
Đáp án cần chọn là: D
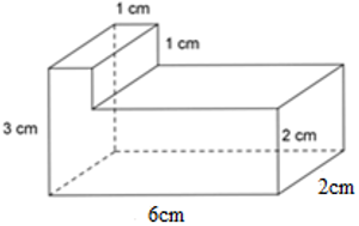
Bài 27: Tính thể tích của hình lăng trụ đứng sau:
A. 16 cm3
B. 20 cm3
C. 26 cm3
D. 22 cm3
Lời giải
Hình lăng trụ đứng đã cho được tạo thành từ 2 hình hộp chữ nhật. Hình hộp chữ nhật thứ nhất có kích thước là 3 cm, 1 cm, 2 cm; hình hộp chữ nhật thứ hai có kích thước là 2 cm; 5 cm; 2m.
Thể tích hình hộp chữ nhật thứ nhất là: V1 = 3.1.2 = 6 cm3
Thể tích hình hộp chữ nhật thứ hai là: V2 = 2.4.2 = 20 cm3
Thể tích hình lăng trụ đứng là: V = V1 + V2 = 6 +20 = 26 cm3
Đáp án cần chọn là: C
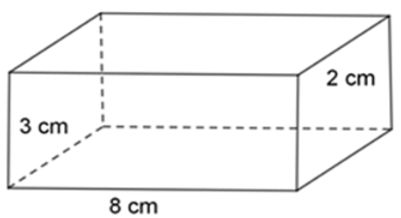
Bài 28: Một hình lăng trụ đứng có đáy là hình chữ nhật có các kích thước 3 cm, 8 cm. Chiều cao của hình lăng trụ đứng là 2 cm. Tính diện tích xung quanh và thể tích của hình lăng trụ đứng.
A. 48 cm2, 46 cm3
B. 48 cm2, 44 cm3
C. 46 cm2, 48 cm3
D. 44 cm2, 48 cm3
Lời giải
Diện tích xung quanh Sxq = 2. (8 + 3).2 = 44 cm2
Thể tích của hình lăng trụ đứng là: V = 8.3.2 = 48 cm3
Đáp án cần chọn là: D
Bài 29: Một hình lăng trụ đứng có đáy là hình chữ nhật có các kích thước 3 cm, 8 cm. Chiều cao của hình lăng trụ đứng là 2 cm. Thể tích của hình lăng trụ đứng là:
A. 46 cm3
B. cm3
C. 48 cm3
D. 50 cm3
Lời giải
Thể tích của hình lăng trụ đứng là: V = 8.3.2 = 48 cm3
Đáp án cần chọn là: C
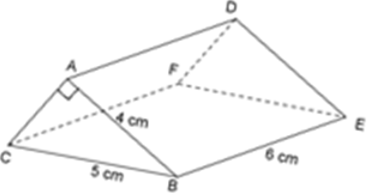
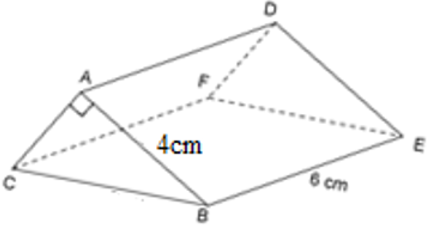
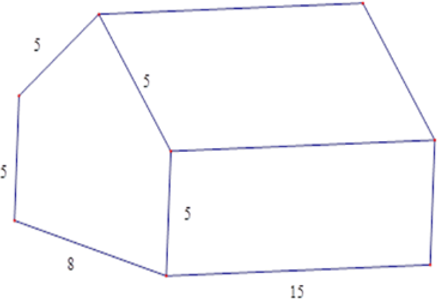
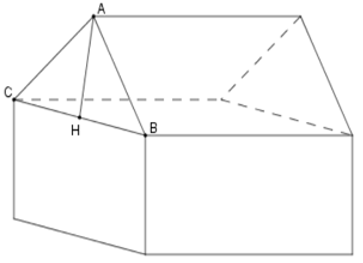
Bài 30: Tính thể tích nhà kho có dạng hình lăng trụ đứng ngũ giác với các kích thước được đo bằng mét.
A. 870 m3
B. 700 m3
C. 680 m3
D. 780 m3
Lời giải
Gọi H là trung điểm BC ⇒ AH ⊥ BC. Ta có BH = 4; AB = 5 m
Thể tích nhà kho bằng: V = 52.15 = 780 (m3)
Đáp án cần chọn là: D
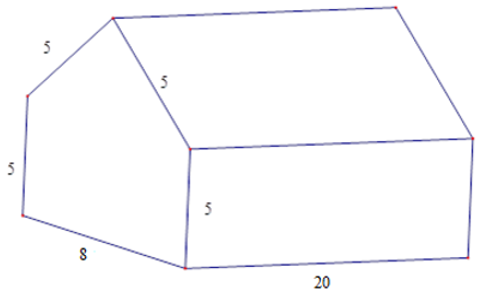
Bài 30: Tính thể tích nhà kho có dạng hình lăng trụ đứng ngũ giác với các kích thước được đo bằng mét.
A. 1040 m3
B. 1400 m3
C. 1004 m3
D. 780 m3
Lời giải
Gọi H là trung điểm BC ⇒ AH ⊥ BC. Ta có BH = 4; AB = 5 m
Thể tích nhà kho bằng: V = 52.20 = 1040 (m3)
Đáp án cần chọn là: A
Bài 31: Không hiển thị
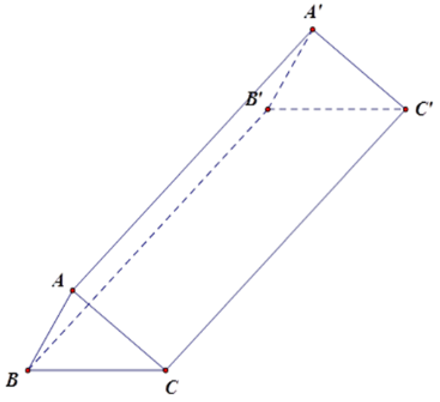
Bài 32: Cho hình lăng trụ đứng ABC.DEF, đáy là tam giác ABC có AB = 6 cm, BC = 8 cm, AC = 10 cm và chiều cao của lăng trụ là 12 cm.
Tam giác ABC là tam giác gì?
A. Vuông tại A
B. Vuông tại B
C. Vuông tại C
D. Đều
Lời giải
Ta có:
AB2 + BC2 = 62 + 82 = 100
AC2 = 102 = 100 ⇒ AB2 + BC2 = AC2
Áp dụng định lý đảo của định lý Pitago ta có tam giác ABC là tam giác vuông tại B
Đáp án cần chọn là: B