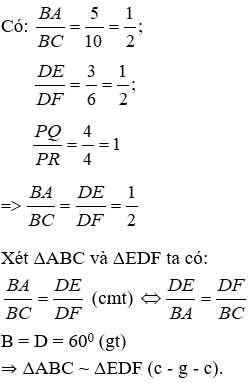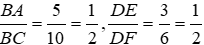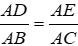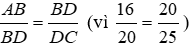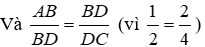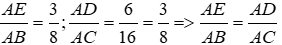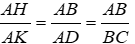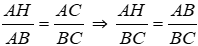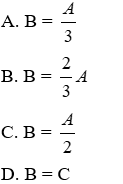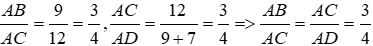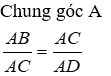Trắc nghiệm Trường hợp đồng dạng thứ hai có đáp án - Toán lớp 8
Trắc nghiệm Trường hợp đồng dạng thứ hai có đáp án
Với bộ bài tập Trắc nghiệm Trường hợp đồng dạng thứ hai Toán lớp 8 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 8.
Bài 1: Hãy chọn câu đúng. Nếu ΔABC và ΔDEF có góc B = D;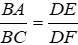 
thì:
A. ΔABC đồng dạng với ΔDEF
B. ΔABC đồng dạng với ΔEDF
C. ΔBCA đồng dạng với ΔDEF
D. ΔABC đồng dạng với ΔFDE
Lời giải
ΔABC và ΔDEF có góc B = D; 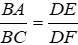thì ΔABC đồng dạng với ΔEDF
Đáp án cần chọn là: B
Bài 2: Cho ΔABC và ΔDEF có góc B = D; 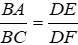, chọn kết luận đúng:
A. ΔABC ~ ΔDEF
B. ΔABC ~ ΔEDF
C. ΔBAC ~ ΔDFE
D. ΔABC ~ ΔFDE
Lời giải
ΔABC và ΔDEF có góc B = D; 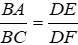thì ΔABC đồng dạng với ΔEDF
Đáp án cần chọn là: B
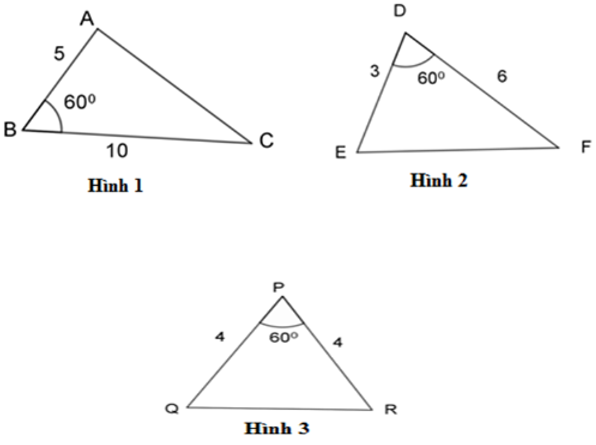
Bài 3: Hãy chỉ ra cặp tam giác đồng dạng với nhau từ các tam giác sau đây:
A. Hình 1 và hình 2
B. Hình 2 và hình 3
C. Hình 1 và hình 3
D. Tất cả đều đúng
Lời giải
Đáp án cần chọn là: A
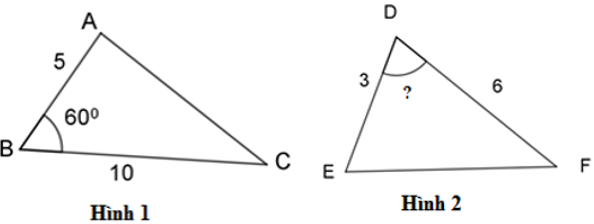
Bài 4: Để hai tam giác ABC và EDF đồng dạng thì số đo góc D trong hình vẽ dưới bằng:
A. 500
B. 600
C. 300
D. 700
Lời giải
Có: 
Để hai tam giác đã cho đồng dạng thì góc ABC = EDF = 600.
Đáp án cần chọn là: B
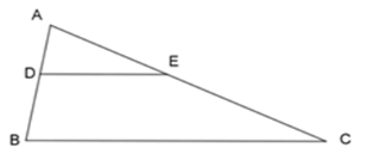
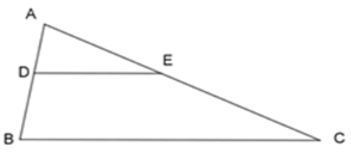
Bài 5: Cho ΔABC, lấy 2 điểm D và E lần lượt nằm bên cạnh AB và AC sao cho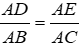 
. Kết luận nào sai?
A. ΔADE ~ ΔABC
B. DE // BC
C.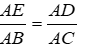 
D. góc ADE = góc ABC
Lời giải
Đáp án cần chọn là: C
Bài 6: Cho ΔABC, trên cạnh AB lấy điểm D khác A, B. Qua D kẻ đường thẳng song song với BC cắt AC tại E. Chọn kết luận sai?
A. ΔADE ~ ΔABC
B. DE // BC
C. 
D. góc ADE = góc ACB
Lời giải
Do DE // BC nên theo định lý Talet đảo ta có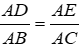 
nên C đúng.
Xét ΔADE và ΔABC ta có:
(cmt)
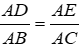
A chung.
⇒ ΔADE ~ ΔABC (c - g - c) nên A đúng
⇒ ADE = ABC (cặp góc tương ứng) nên D sai.
⇒ 
Đáp án cần chọn là: D
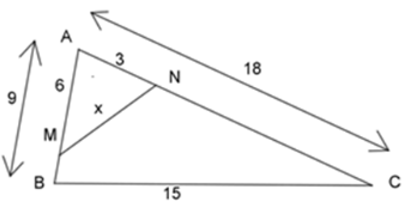
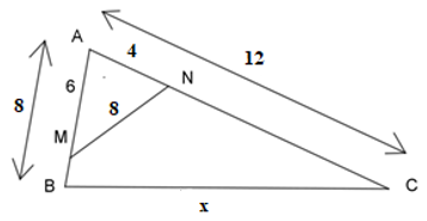
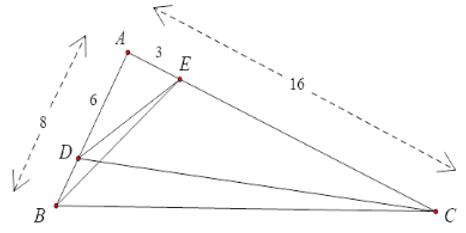
Bài 7: Cho hình vẽ dưới đây, tính giá trị của x?
A. x = 6
B. x = 5
C. x = 8
D. x = 9
Lời giải
Đáp án cần chọn là: B
Bài 8: Cho hình vẽ dưới đây, tính giá trị của x?
A. x = 4
B. x = 16
C. x = 10
D. x = 14
Lời giải
Đáp án cần chọn là: B
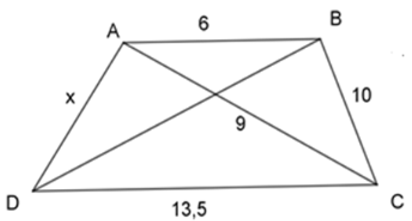
Bài 9: Với AB // CD thì giá trị của x trong hình vẽ dưới đây là
A. x = 15
B. x = 16
C. x = 7
D. x = 8
Lời giải
Đáp án cần chọn là: A
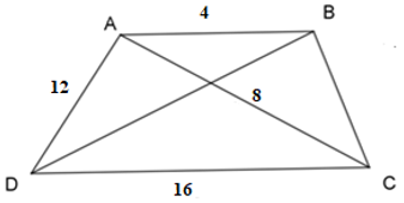
Bài 10: Cho hình thang ABCD có: AB // CD, AB = 4, CD = 16, AC = 8, AD = 12. Độ dài BC là:
A. 8
B. 13
C. 12
D. 6
Lời giải
Đáp án cần chọn là: D
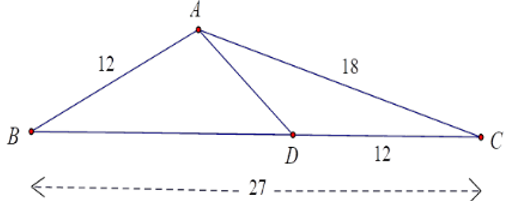
Bài 11: Cho tam giác ABC có AB = 12cm, AC = 18cm, BC = 27cm. Điểm D thuộc cạnh BC sao cho CD = 12cm. Tính độ dài AD.
A. 12cm
B. 6cm
C. 10cm
D. 8cm
Lời giải
Đáp án cần chọn là: D
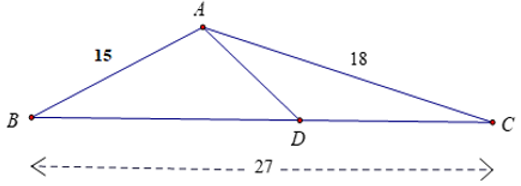
Bài 12: Cho tam giác ABC có AB = 15cm, AC = 18cm, BC = 27cm. Điểm D thuộc cạnh BC sao cho 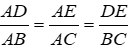. Độ dài AD là:
A. 12cm
B. 6cm
C. 10cm
D. 8cm
Lời giải
Đáp án cần chọn là: C
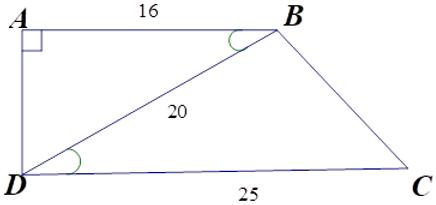
Bài 13: Cho hình thang vuông ABCD (A = D = 900) có AB = 16cm, CD = 25cm, BD = 20cm.
1. Tam giác ABD đồng dạng với tam giác nào dưới đây?
A. ΔBDC
B. ΔCBD
C. ΔBCD
D. ΔDCB
Lời giải
ΔABD và ΔBDC có góc ABD = BDC (hai góc ở vị trí so le trong bằng nhau do AB // CD);
Và 
Do đó ΔABD ~ ΔBDC (c.g.c)
Đáp án cần chọn là: A
2. Độ dài cạnh BC là
A. 10cm
B. 12cm
C. 15cm
D. 9cm
Lời giải
Vì ΔABD ~ ΔBDC (cmt) nên góc A = DBC.
Ta có A = 900 nên DBC = 900. Theo định lí Pytago, ta có
BC2 = CD2 - BD2 = 252 - 202 = 152. Vậy BC = 15cm
Đáp án cần chọn là: C
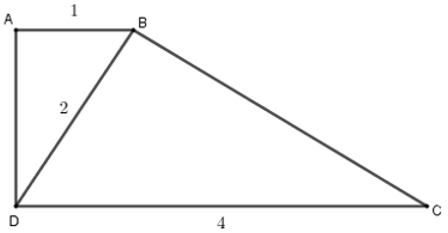
Bài 14: Cho hình thang vuông ABCD (A = D = 900) có AB = 1cm, CD = 4cm, BD = 2cm.
1.Chọn kết luận sai?
A. ΔABD ~ ΔBDC
B. BDC = 900
C. BC = 2AD
D. BD vuông góc BC
Lời giải
ΔABD và ΔBDC có: ABD = BDC (hai góc ở vị trí so le trong bằng nhau do AB // CD)
Do đó ΔABD ~ ΔBDC (c.g.c) nên A đúng.
⇒ ABD = BDC < 900 nên B sai.
ΔABD ~ ΔBDC ⇒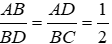 
(cạnh t/u) ⇔ BC = 2AD nên C đúng.
BAD = DBC = 900 nên BD ⊥ BC hay D đúng
Vậy chỉ có B sai.
Đáp án cần chọn là: B
2. Độ dài cạn BC là (làm tròn đến hai chữ số thập phân)
A. 3cm
B. 4cm
C. 4,36cm
D. 3,46cm
Lời giải
Tam giác BDC vuông tại B (theo câu trên), định lý Pitago ta có:
BD2 + BC2 = CD2 ⇔ 22 + BC2 = 42 ⇔ BC2 = 12 ⇒ BC ≈ 3,46
Đáp án cần chọn là: D
Bài 15: Cho tam giác ABC có AB = 8cm, AC = 16cm. Điểm D thuộc cạnh AB sao cho BD = 2cm. Điểm E thuộc cạnh AC sao cho CE = 13cm.
1. Chọn câu đúng.
A. ΔEDA ~ ΔABC
B. ΔADE ~ ΔABC
C. ΔAED ~ ΔABC
D. ΔDEA ~ ΔABC
Lời giải
Ta có: 
Xét ΔAED và ΔABC có A chung và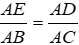 
(cmt)
Nên ΔAED ~ ΔABC (c.g.c)
Đáp án cần chọn là: C
2. Chọn câu sai.
A. góc ABE = góc ACD
B. AE.CD = AD. BC
C. AE.CD = AD.BE
D. AE.AC = AD.AB
Lời giải
+ Xét ΔABE và ΔACD có A chung và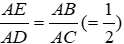 
nên
ΔABE ~ ΔACD (c - g - c) suy ra góc ABE = góc ACD (hai góc tương ứng) và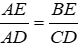 
⇒ AE.CD = AD.BE
+ ΔAED ~ ΔABC (cmt) nên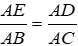 
AE.AC = AB.AD
Nên A, C, D đúng, B sai.
Đáp án cần chọn là: B
Bài 16: Ko load đc đề
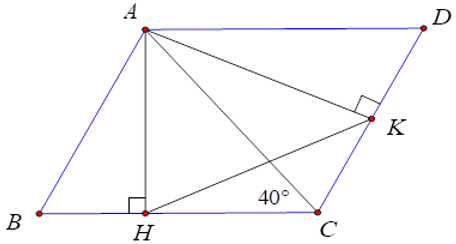
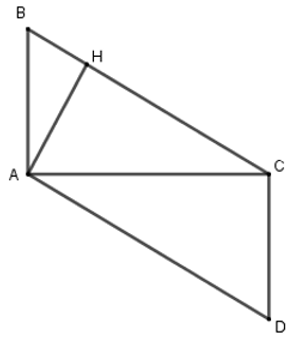
Bài 17: Cho tam giác nhọn ABC có C = 400. Vẽ hình bình hành ABCD. Gọi AH, AK theo thứ tự là các đường cao của các tam giác ABC, ACD. Tính số đo góc AKH.
A. 300
B. 400
C. 450
D. 500
Lời giải
Vì AD.AH = AB.AK (=SABCD) nên 
Ta lại có AB // CD (vì ABCD là hình bình hành) mà AK ⊥ DC ⇒ AK ⊥ AB
⇒ BAK = 900.
Từ đó góc HAK = ABC (cùng phụ với BAH)
Nên ΔAKH ~ ΔBCA (c.g.c) ⇒ góc AKH = góc ACB = 400.
Đáp án cần chọn là: B
Bài 18: Cho tam giác ABC vuông tại A, gọi H là hình chiếu của A lên BC. Dựng hình bình hành ABCD. Chọn kết luận không đúng:
A. ΔABC ~ ΔHCA
B. ΔADC ~ ΔCAH
C. ΔABH ~ ΔADC
D. ΔABC = ΔCDA
Lời giải
Xét ΔABC và ΔCDA có:
AB = CD (t/c)
AC chung
BAC = DCA = 900
Suy ra ΔABC = ΔCDA (c-g-c) nên D đúng.
Suy ra ΔABC ~ ΔHAC (c - g - c) nên A sai
Ngoài ra, ΔADC = ΔCBA và ΔCBA ~ ΔCAH hay ΔADC ~ ΔCAH nên B đúng
Từ 
Xét ΔABH và ΔCBA có:
Chung B
⇒ ΔABH ~ ΔCBA (c-g-c)
Mà ΔADC = ΔCBA nên ΔABH ~ ΔADC hay C đúng
Vậy chỉ có A sai.
Đáp án cần chọn là: A
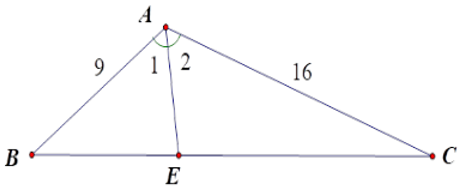
Bài 19: Cho tam giác ABC có AB = 9cm, AC = 16cm, BC = 20cm. Khi đó:
Lời giải
Kẻ đường phân giác AE của góc BAC. Theo tính chất đường phân giác, ta có:
Do đó ΔACB ~ ΔECA (c.g.c) suy ra B = A2, tức là B = A/2
Đáp án cần chọn là: C
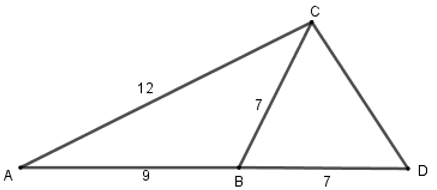
Bài 20: Cho tam giác ABC có AB = 9cm, AC = 12cm, BC = 7cm. Chọn kết luận đúng.
A. góc ABC = 2. góc BAC
B. góc ABC = góc ACB
C. góc ABC = 2. góc ACB
D. góc ABC = 1350
Lời giải
Ta có: 
Xét tam giác ABC và ACD có:
⇒ ΔABC ~ ΔACD (c.g.c) ⇒ góc ACB = góc ADC = góc BDC (góc tương ứng) (1)
Mà ΔBCD có: BC = BD nên là tam giác cân ⇒góc ADC = BCD
Lại có: góc ABC = góc BCD + góc BDC = 2. góc BDC (2)
Từ (1) và (2) suy ra: góc ABC = 2. góc ACB
Đáp án cần chọn là: C
