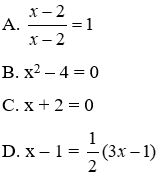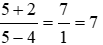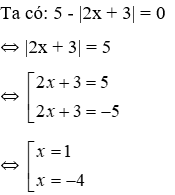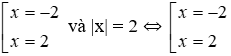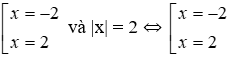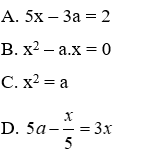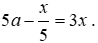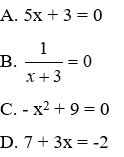Trắc nghiệm Mở đầu về phương trình có đáp án - Toán lớp 8
Trắc nghiệm Mở đầu về phương trình có đáp án
Với bộ bài tập Trắc nghiệm Mở đầu về phương trình Toán lớp 8 chọn lọc, có đáp án sẽ giúp học sinh hệ thống lại kiến thức bài học và ôn luyện để đạt kết quả cao trong các bài thi môn Toán lớp 8.
Bài 1: Hai phương trình tương đương là hai phương trình có
A. Một nghiệm giống nhau
B. Hai nghiệm giống nhau
C. Tập nghiệm giống nhau
D. Tập nghiệm khác nhau
Lời giải
Hai phương trình tương đương là hai phương trình có cùng tập nghiệm
Đáp án cần chọn là: C
Bài 2: Chọn khẳng định đúng
A. Hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm
B. Hai phương trình được gọi là tương đương nếu chúng có cùng số nghiệm
C. Hai phương trình được gọi là tương đương nếu chúng có chung một nghiệm
D. Hai phương trình được gọi là tương đương nếu chúng cùng điều kiện xác định
Lời giải
Hai phương trình được gọi là tương đương nếu chúng có cùng tập nghiệm
Đáp án cần chọn là: A
Bài 3: Số 
là nghiệm của phương trình nào dưới đây?
A. x - 1 =
B. 4x2 – 1 = 0
C. x2 + 1 = 5
D. 2x – 1 = 3
Lời giải
Thay x = vào từng phương trình ta được
+) 
(L) nên x = không là nghiệm của phương trình x – 1 =
+) 
(L) nên x = không là nghiệm phương trình x2 + 1 = 5
+) 
(L) nên x = không là nghiệm của phương trình 2x – 1 = 3
+) 4x2 – 1 = 0
⇒ 
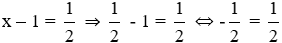
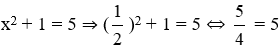
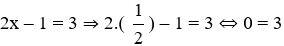
(N) nên x = là nghiệm của phương trình 4x2 – 1 = 0
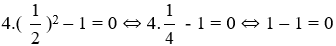
Đáp án cần chọn là: B
Bài 4: Phương trình nào sau đây nhận x = 2 làm nghiệm?
Lời giải
Đáp án A loại vì x = 2 không thỏa mãn điều kiện xác định
Đáp án B: 22 – 4 = 4 – 4 = 0 nên x = 2 là nghiệm của phương trình đáp án B.
Đáp án C: Dễ thấy 2 + 2 = 4 ≠ 0 nên x = 2 không là nghiệm của phương trình đáp án C
Đáp án D: Thay x = 2 ta được VT = 2 – 1 = 1 ≠ (3.2 - 1) = VP nên không là nghiêm
Đáp án cần chọn là: B
Bài 5: Chọn khẳng định đúng
A. 3 là nghiệm của phương trình x2 – 9 = 0
B. {3} là tập nghiệm của phương trình x2 – 9 = 0
C. Tập nghiệm của phương trình (x + 3)(x – 3) = x2 – 9 là Q
D. x = 2 là nghiệm duy nhất của phương trình x2 – 4 = 0
Lời giải
+ Ta có x2 – 9 = 0 ⇔ x2 = 9 ⇔ x = ±3. Nên x = 3 là nghiệm của phương trình x2 – 9 = 0 và tập nghiệm của phương trình là {3; -3}. Suy ra A đúng, B sai.
+ Xét (x + 3)(x – 3) = x2 – 9 ⇔ x2 – 9 = x2 – 9 (luôn đúng) nên tập nghiệm của phương trình là R, suy ra C sai.
+ Xét x2 – 4 = 0 ⇔ x2 = 4 ⇔ x = ±2 ⇒ phương trình có hai nghiệm x = 2; x = -2 nên D sai
Đáp án cần chọn là: A
Bài 6: Cho các mệnh sau:
(I) 5 là nghiệm của phương trình 2x – 3 =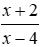 
(II) Tập nghiệm của phương trình 7 – x = 2x – 8 là x = 5
(III) Tập nghiệm của phương trình 10 – 2x = 0 là S = {5}.
Số mệnh đề đúng là:
A. 1
B. 0
C. 2
D. 3
Lời giải
Mệnh đề (I): Thay x = 5 vào phương trình ta được VT = 2.5 – 3 = 7; VP = 
Do đó VT = VP hay x = 5 là nghiệm của phương trình
Do đó (I) đúng
Mệnh đề (II): Sai do kí hiệu
7 – x = 2x – 8 ⇔ x = 5 nên phương trình có tập nghiệm S = {5}
Vậy có 2 mệnh đề đúng.
Đáp án cần chọn là: C
Bài 7: Phương trình nào sau đây vô nghiệm?
A. x – 1 = 0
B. 4x2 + 1 = 0
C. x2 – 3 = 6
D. x2 + 6x = -9
Lời giải
+) x – 1 = 0 ⇔ x = 1Ø
+) 4x2 + 1 = 0 ⇔ 4x2 = -1 (vô nghiệm vì 4x2 ≥ 0; Ɐx)
+) x2 – 3 = 6 ⇔ x2 = 9 ⇔ x = ± 3
+) x2 + 6x = -9 ⇔ x2 + 6x + 9 = 0 ⇔ (x + 3)2 = 0 ⇔ x + 3 = 0 ⇔ x = -3
Vậy phương trình 4x2 + 1 = 0 vô nghiệm
Đáp án cần chọn là: B
Bài 8: Phương trình nào sau đây vô nghiệm?
A. 2x – 1 = 0
B. -x2 + 4 = 0
C. x2 + 3 = -6
D. 4x2 +4x = -1
Lời giải
+) 2x – 1 = 0 ⇔ x =
+) -x2 + 4 = 0 ⇔ x2 = 4 ⇔ x = ±2
+) x2 + 3 = -6 ⇔ x2 = -9 (vô nghiệm vì -9< 0)
+) 4x2 + 4x = -1 ⇔ 4x2 +4x + 1 = 0 ⇔ (2x + 1)2 = 0 ⇔ 2x + 1 = 0 ⇔ x = -
Đáp án cần chọn là: C
Bài 9: Tập nghiệm của phương trình 3x – 6 = x – 2 là
A. S = {2}
B. S = {-2}
C. S = {4}
D. S = Ø
Lời giải
Ta có 3x – 6 = x – 2 ⇔ 3x – x = -2 + 6 ⇔ 2x = 4 ⇔ x = 2
Tập nghiệm của phương trình là S = {2}
Đáp án cần chọn là: A
Bài 10: Phương trình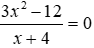 
có tập nghiệm là
A. S = {±4}
B. S = {±2}
C. S = {2}
D. S = {4}
Lời giải
ĐKXĐ: x + 4 ≠ 0 ⇔ x ≠ -4
Phương trình ⇔ 3x2 – 12 = 0 ⇔ x2 = 4 ⇔ x = ±2 (tm)
Vậy tập nghiệm của phương trình là S = {±2}
Đáp án cần chọn là: B
Bài 11: Có bao nhiêu nghiệm của phương trình |x + 3| = 7?
A. 2
B. 1
C. 0
D. 4
Lời giải
Ta có: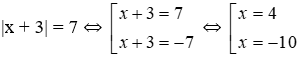 
Vậy phương trình có hai nghiệm x = 4; x = -10
Đáp án cần chọn là: A
Bài 12: Số nghiệm của phương trình 5 - |2x + 3| = 0 là
A. 2
B. 1
C. 0
D. 4
Lời giải
Vậy phương trình có hai nghiệm x = 1; x = -4
Đáp án cần chọn là: A
Bài 13: Hai phương trình nào sau đây là hai phương trình tương đương?
A. x – 2 =4 và x + 1 = 2
B. x = 5 và x2 = 25
C. 2x2 – 8 = 0 và |x| = 2
D. 4 + x = 5 và x3 – 2x = 0
Lời giải
+) Xét x – 2 = 4 ⇔ x = 6 và x + 1 = 2 ⇔ x = 1 nên hai phương trình x – 2 =4 và x + 1 = 2 không tương đương
+) Xét phương trình x2 = 25 ⇔ x = ±5 nên phương trình x2 = 25 có hai nghiệm. Suy ra hai phương trình x = 5 và x2 = 25 không tương đương.
+) Xét phương trình 4 + x = 5 ⇔ x = 1, mà x = 1 không là nghiệm của phương trình x3 – 2x = 0 (vì 13 – 2.1= -1 ≠ 0) nên hai phương trình 4 + x = 5 và x3 – 2x = 0 không tương đương.
+) Xét phương trình 2x2 – 8 = 0 ⇔ 2x2 = 8 ⇔ x2 = 4 ⇔ 
Nhận thấy hai phương trình trên có cùng tập nghiệm {2; -2} nên chúng tương đương.
Đáp án cần chọn là: C
Bài 14: Số cặp phương trình tương đương trong các cặp phương trình sau là:
(I) x – 2 =4 và x + 1 = 2
(II) x = 5 và x2 = 25
(III) 2x2 – 8 = 0 và |x| = 2
(IV) 4 + x = 5 và x3 – 2x = 0
A. 1
B. 2
C. 3
D. 4
Lời giải
+) Xét x – 2 = 4 ⇔ x = 6 và x + 1 = 2 ⇔ x = 1 nên hai phương trình x – 2 =4 và x + 1 = 2 không tương đương
+) Xét phương trình x2 = 25 ⇔ x = ±5 nên phương trình x2 = 25 có hai nghiệm. Suy ra hai phương trình x = 5 và x2 = 25 không tương đương.
+) Xét phương trình 4 + x = 5 ⇔ x = 1, mà x = 1 không là nghiệm của phương trình x3 – 2x = 0 (vì 13 – 2.1= -1 ≠ 0) nên hai phương trình 4 + x = 5 và x3 – 2x = 0 không tương đương.
+) Xét phương trình 2x2 – 8 = 0 ⇔ 2x2 = 8 ⇔ x2 = 4 ⇔ 
Nhận thấy hai phương trình trên có cùng tập nghiệm {2; -2} nên chúng tương đương.
Vậy chỉ có 1 cặp phương trình tương đương trong các cặp đã cho
Đáp án cần chọn là: A
Bài 15: Phương trình nào dưới đây nhận x = a (a là hằng số khác 0 và 1) làm nghiệm
Lời giải
Thay x = a vào từng phương trình ta được
+) 5.a – 3a = 2 ⇔ 2a = 2 ⇔ a = 1 (loại) nên x = a không là nghiệm của phương trình 5x – 3a = 2
+) a2 = a ⇔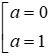 
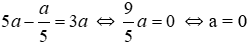
(loại) nên x = a không là nghiệm của phương trình x2 = a
+) 
(loại) nên x = a không là nghiệm của phương trình 
+) a2 – a.a = a2 – a2 = 0 nên x = a là nghiệm của phương trình x2 – a.x = 0
Đáp án cần chọn là: B
Bài 16: Phương trình nào dưới đây nhận x = -3 là nghiệm duy nhất?
Lời giải
Đáp án A: 5x + 3 = 0 ⇔ 5x = -3 ⇔ x =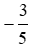 
(loại)
Đáp án B: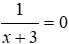 
có ĐKXĐ: x + 3 ≠ 0 ⇔ x ≠ - 3 nên không nhận -3 làm nghiệm (loại)
Đáp án C: -x2 + 9 = 0 ⇔ x2 = 9 ⇔ x = ±3 nên phương trình có hai nghiệm x = ±3 (loại).
Đáp án D: 7 + 3x = -2 ⇔ 3x = -9 ⇔ x = -3 nên phương nhận x = - 3 làm nghiệm duy nhất.
Đáp án cần chọn là: D
Bài 17: Chọn khẳng định đúng
A. Hai phương trình x2 – 2x + 1 = 0 và x2 – 1 = 0 là hai phương trình tương đương
B. Hai phương trình x2 – 2x + 1 = 0 (1) và x2 – 1 = 0 (2) không tương đương vì x = 1 là nghiệm của phương trình (1) nhưng không là nghiệm của phương trình (2).
C. Hai phương trình x2 – 2x + 1 = 0 (1) và x2 – 1 = 0 (2) không tương đương vì x = -1 là nghiệm của phương trình (1) nhưng không là nghiệm của phương trình (2).
D. Hai phương trình x2 – 2x + 1 = 0 (1) và x2 – 1 = 0 (2) không tương đương vì x = -1 là nghiệm của phương trình (2) nhưng không là nghiệm của phương trình (1).
Lời giải
+ Xét phương trình (1): x2 – 2x + 1 = 0 ⇔ (x – 1)2 = 0 ⇔ x – 1 = 0 ⇔ x = 1
+ Xét phương trình (2): x2 – 1 = 0 ⇔ x2 = 1 ⇔ x = ±1
Nhận thấy x = -1 là nghiệm của phương trình (1) nên hai phương trình (1) và (2) không tương đương
Đáp án cần chọn là: D
Bài 18: Chọn khẳng định đúng
A. Hai phương trình x2 + 2x + 1 = 0 và x2 – 1 = 0 là hai phương trình tương đương
B. Hai phương trình x2 + 2x + 1 = 0 (1) và x2 – 1 = 0 (2) không tương đương vì x = 1 là nghiệm của phương trình (1) nhưng không là nghiệm của phương trình (2).
C. Hai phương trình x2 + 2x + 1 = 0 (1) và x2 – 1 = 0 (2) không tương đương vì x = 1 là nghiệm của phương trình (2) nhưng không là nghiệm của phương trình (1).
D. Hai phương trình x2 + 2x + 1 = 0 (1) và x2 – 1 = 0 (2) tương đương vì x = -1 là nghiệm chung của cả hai phương trình.
Lời giải
+ Xét phương trình (1): x2 + 2x + 1 = 0 ⇔ (x + 1)2 = 0 ⇔ x + 1 = 0 ⇔ x = -1
+ Xét phương trình (2): x2 – 1 = 0 ⇔ x2 = 1 ⇔ x = ±1
Nhận thấy x = 1 là nghiệm của phương trình (2) nhưng không là nghiệm của phương trình (1) nên hai phương trình (1) và (2) không tương đương
Đáp án cần chọn là: C
Bài 19: Số x0 được gọi là nghiệm của phương trình A(x) = B(x) khi
A. A(x0) < B(x0)
B. A(x0) > B(x0)
C. A(x0) = -B(x0)
D. A(x0) = B(x0)
Lời giải
Giá x0 thỏa mãn A(x0) = B(x0) được gọi là nghiệm của phương trình A(x) = B(x)
Đáp án cần chọn là: D
Bài 20: Nếu phương trình P(x) = m có nghiệm x = x0 thì x0 thỏa mãn:
A. P(x) = x0
B. P(m) = x0
C. P(x0) = m
D. P(x0) = -m
Lời giải
Nếu phương tình P(x) = m có nghiệm x = x0 thì P(x0) = m
Đáp án cần chọn là: C
