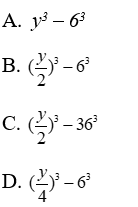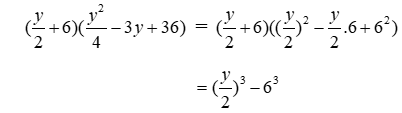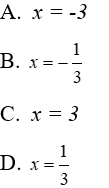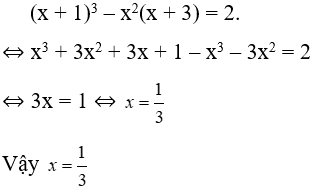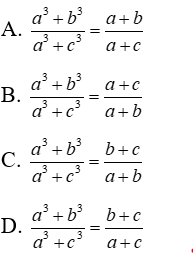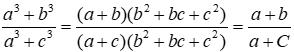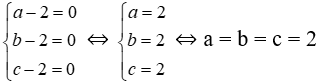Trắc nghiệm Những hằng đẳng thức đáng nhớ (phần 2) có đáp án - Toán lớp 8

Lời giải

Ta có (A + B)³ = A³ + 3A²B + 3AB² + B³ nên phương án C sai, A đúng.

(A - B)³ = A³ - 3A²B + 3AB² - B³ nên phương án B sai, D sai.

Đáp án cần chọn là: A

Lời giải

Ta có (x – 2y)³ = x³ – 3.x².2y + 3x.(2y)² – (2y)³ = x³ – 6x²y + 12xy² – 8y³

Đáp án cần chọn là: B

Lời giải

Ta có A³ + B³ = (A + B)(A² – AB + B²) và A³ - B³ = (A - B)(A² + AB + B²) nên A, B đúng.

Vì A + B = B + A ⇒ (A + B)³ = (B + A)³ nên C đúng

Vì A – B = - (B – A) ⇒ (A – B)³ = -(B – A)³ nên D sai

Đáp án cần chọn là: D

Lời giải

Ta có 8 + 12y + 6y² + y³ = 2³ + 3.2²y + 3.2.y² + y³ = (2 + y)³ ≠ (8 + y³) nên A sai

+ Xét (2x – y)³ = (2x³ – 3(2x)².y + 3.2x.y² – y³

= 8x³ – 12x²y + 6xy – y³ ≠ 2x³ – 6x²y + 6xy – y³ nên C sai

+ Xét (3a + 1)³ = (3a)³ + 3.(3a)².1 + 3.3a.1² + 1

                   = 27a³ + 27a² + 9a + 1 ≠ 3a³ + 9a² + 3a + 1 nên D sai

+ Xét a³ + 3a² + 3a + 1 = (a + 1)³ nên B đúng

Đáp án cần chọn là: B

Lời giải

Ta có (-b – a)³ = [-(a + b)³] = -(a + b)³

                   = -(a³ + 3a²b + 3ab² + b³)

                   =  -a³ - 3a²b - 3ab² - b³

                   = -a³ – 3ab(a + b) – b³ nên A đúng

+ Xét (c – d)³ = c³ – 3c²d + 3cd² + d³ = c³ – d³ + 3cd(d – c) nên B đúng

+ Xét (y – 1)³ = y³ – 3y².1 + 3y.1² – 1³ = y³ – 1 – 3y(y – 1) nên D đúng

+ Xét (y – 2)³ = y³ – 3y².2 +3y.2² – 2³ = y³ – 6y² + 12y – 8

= y³ – 8 – 6y(y – 2) ≠ y³ – 8 – 6y(y + 2) nên C sai

Đáp án cần chọn là: C

Lời giải

Ta có x³ + 12x² + 48x + 64 = x³ + 3x².4 + 3.x.4² + 4³ = (x + 4)³

Đáp án cần chọn là: A

Lời giải

Ta có 8x³ + 36x² + 54x + 27 = (2x)³ + 3(2x)².3 + 3.2x.3² + 3³ = (2x + 3)³

Đáp án cần chọn là: B

Lời giải

Ta có x³ – 6x² + 12x – 8 = x³ – 3.x².2 + 3.x.2² – 2³ = (x – 2)³

Đáp án cần chọn là: D

Lời giải

Ta có 8x³ – 12x²y + 6xy² – y³ = (2x)³ – 3.(2x)²y + 3.2x.y² – y³ = (2x – y)³

Đáp án cần chọn là: A

Lời giải

Ta có  (x – 3y)(x² + 3xy + 9y²) = (x – 3y)(x + x.3y + (3y)² = x³ – (3y)³

Đáp án cần chọn là: C

Lời giải

Ta có (3x – 4)(9x² + 12x + 16) = (3x – 4)((3x)² + 3x.4 + 4²) = (3x)³ – 4³

Đáp án cần chọn là: D

Lời giải

Ta có (x² + 3)(x⁴ – 3x² + 9) = (x² + 3)((x²)² – 3.x² + 3²) = (x²)³ + 3³

Đáp án cần chọn là: A

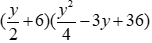
Lời giải

Ta có:

Đáp án cần chọn là: B

Lời giải

Ta có x³ + 3x² + 3x + 1 = 0 ⇔ (x + 1)³ = 0

⇔ x + 1 = 0 ⇔ x = -1

Vậy x = -1

Đáp án cần chọn là: A

Lời giải

Ta có x³ – 12x² + 48x – 64 = 0

⇔ x³ – 3.x².4 + 3.x.4² – 4³ = 0

⇔ (x – 4)³ = 0 ⇔ x – 4 = 0 ⇔ x = 4

Vậy x = 4

Đáp án cần chọn là: B

Lời giải

Ta có (x + 2) (x² – 2x + 4) – x(x² – 2) = 14

⇔ x³ + 2³ – (x³ – 2x) = 14

⇔ x³ + 8 – x³ + 2x = 14

⇔ 2x = 6 ⇔ x = 3

Vậy x = 3

Đáp án cần chọn là: C

Lời giải

Ta có:

Đáp án cần chọn là: D

Lời giải

Ta có A = x³ – 3x² + 3x = x³ – 3x² + 3x – 1 + 1 = (x – 1)³ + 1

Thay x = 1001 vào A = (x – 1)³ + 1 ta được

A = (1001 – 1)³ + 1 suy ra A = 1000³ + 1

Đáp án cần chọn là: D

Lời giải

Ta có B = x³ – 6x² + 12x + 10

          = x³ – 3x².2 + 3x.2² – 8 + 18 = (x – 2)³ + 18

Thay x = 1002 vào B = (x – 2)³ + 18 ta được

B = (1002 – 2)³ + 18 = 1000³ + 18     

Đáp án cần chọn là: A

Lời giải

Ta có M = (2x + 3)(4x² – 6x + 9) – 4(2x³ – 3)

          = (2x + 3)[(2x)² – 2x.3 + 3²] – 8x³ + 12

          = (2x)³ = 3² – 8x³ + 12 = 8x³ + 27 – 8x³ + 12 = 39

Vậy giá trị của M là một số lẻ

Đáp án cần chọn là: A

Lời giải

Ta có H = (x + 5)(x² – 5x + 25) – (2x + 1)³ + 7(x – 1)³ – 3x(-11x + 5)

          = x³ + 5³ – (8x³ + 3.(2x)².1 + 3.2x.1² + 1) + 7(x³ – 3x² + 3x – 1) + 33x² – 15x

          = x³ + 125 – 8x³ – 12x² – 6x – 1 + 7x³ – 21x² + 21x – 7 + 33x² – 15x

          = (x³ – 8x³ + 7x³) + (-12x² – 21x² + 33x²) + (-6x + 21x – 15x) + 125 – 1 – 7

          = 117

Vậy giá trị của M là một số lẻ

Đáp án cần chọn là: A

Lời giải

Ta có (x + y)³ = x³ + 3x²y + 3xy² + y³

⇔ x³ + y³ = (x + y)³ – (3x²y + 3xy²)

          = (x + y)³ – 3xy(x + y)

Và (x + y)² = x² + 2xy + y² ⇔ x² + y² = (x + y)² – 2xy

Khi đó P = -2(x³ + y³) + 3(x² + y²)

                   = -2[(x + y)³ – 3xy(x + y)] + 3[(x + y)² – 2xy]

Vì x + y = 1 nên ta có

P = -2(1 – 3xy) + 3(1 – 2xy)

= -2 + 6xy + 3 – 6xy = 1

Vậy P = 1

Đáp án cần chọn là: B

Lời giải

Ta có (a + b)³ = a³ + 3a²b + 3ab² + b³ = a³ + b³ + 3ab(a + b)

Suy ra a³ + b³ = (a + b)³ – 3ab(a + b)

Hay Q = (a + b)³ – 3ab(a + b)

Thay a + b = 5 và a.b = -3 vào Q = (a + b)³ – 3ab(a + b) ta được

Q = 5³ – 3.(-3).5 = 170

Vậy Q = 170

Đáp án cần chọn là: A

Lời giải

Ta có

P = (4x + 1)³ – (4x + 3)(16x² + 3)

= (4x)³ + 3.(4x)².1 + 3.4x.1² + 1³ – (64x³ + 12x + 48x² + 9)

= 64x³ + 48x² + 12x + 1 – 64x³ – 12x – 48x² – 9 = -8

Nên P = -8

Q = (x – 2)³ – x(x + 1)(x – 1) + 6x(x – 3) + 5x

= x³ – 3.x².2 + 3x.2² – 2³ – x(x² – 1) + 6x² – 18x + 5x

= x³ – 6x² + 12x – 8 – x³ + x + 6x² – 18x + 5x = -8

⇒ Q = -8

Vậy P = Q

Đáp án cần chọn là: A

Lời giải

Ta có

M = 8(x – 1)(x² + x + 1) – (2x – 1)(4x² + 2x + 1)

= 8(x³ – 1) – ((2x)³ – 1)

= 8x³ – 8 – 8x³ + 1 = -7 nên M = -7

N = x(x + 2)(x – 2) – (x + 3)(x² – 3x + 9) – 4x

= x(x² – 4) – (x³ + 3³) + 4x

= x³ – 4x – x³ – 27 + 4x = -27

⇒ N = -27

Vậy M = N + 20

Đáp án cần chọn là: D

Lời giải

Ta có E = (x + 1)(x² – x + 1) – (x – 1)(x² + x + 1)

          = x³ + 1 – (x³ – 1) = x³ + 1 – x³ + 1 = 2

Vậy E = 2

Đáp án cần chọn là: A

Lời giải

Ta có A = (x² – 3x + 9)(x + 3) – (54 + x³)

A = (x² – 3x + 3²)(x + 3) – (54 + x³)

A = x³ + 3³ – 54 – x³

A = 27 – 54 = -27

Vậy A = -27

Đáp án cần chọn là: B

Lời giải

Ta có (a + b)³ = a³ + 3a²b + 3ab² + b³ = a³ + b³ + 3ab(a + b)

⇒ a³ + b³ = (a + b)³ – 3ab(a + b)

Từ đó B = a³ + b³ + c³ – 3abc

          = (a + b)³ – 3ab(a + b) + c³ – 3abc

          = [(a+b)³ + c³] – 3ab(a + b +c)

          = (a + b + c)[(a + b)² – (a + b)c + c²] – 3ab(a + b + c)

Mà a + b + c = 0 nên

B = 0.[(a + b)² – (a + b)c + c²] – 3ab.0 = 0

Vậy B = 0

Đáp án cần chọn là: A

Lời giải

Ta có A = 8x³ – 12x²y + 6xy² – y³ + 12x² – 12xy + 3y² + 6x – 3y + 11

          = (2x)³ – 3.(2x)².y + 3.2x.y + y³ + 3(4x² – 4xy + y²) + 3(2x – y) + 11

          = (2x – y)³ + 3(2x – y)² + 3(2x – y) + 1 + 10

          = (2x – y + 1)³ + 10

Thay 2x – y = 9 vào A = (2x – y + 1)³ + 10 ta được A = (9 + 1)³ + 10 = 1010

Vậy A = 1010

Đáp án cần chọn là: C

Lời giải

Ta có A = 1³+ 2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³ + 10³

          = (1³ + 10³) + (2³ + 9³) + (3³ + 8³) + (4³ + 7³) + (5³ + 6³)

          = 11(1² – 10 + 10²) + 11(2² – 2.9 + 9²) + … + 11(5² – 5.6 + 6²)

Vì mỗi số hạng trong tổng đều chia hết cho 11 nên A ⁝ 11.

Lại có A = 1³+ 2³ + 3³ + 4³ + 5³ + 6³ + 7³ + 8³ + 9³ + 10³

          = (1³ + 9³) + (2³ + 8³) + (3³ + 7³) + (4³ + 6³) + (5³ + 10³)

          = 10(1² – 9 + 9²) + 10(2² – 2.8 + 8²) + … + 5³ + 10³

Vì mỗi số hạng trong tổng đều chia hết cho 5 nên A ⁝ 5.

Vậy A chia hết cho cả 5 và 11

Đáp án cần chọn là: C

Lời giải

Ta có a³ + b³ = (a + b)(a² – ab + b²) mà a = b + c nên

a³ + b³ = (a + b)(a² – ab + b²)

= (a + b)[(b + c)² – (b + c)b + b²]

= (a + b)(b² + 2bc + c² – b² – bc + b²)

= (a + b)(b² + bc + c²)

Tương tự ta có

a³ + c³ = (a + c)(a² – ac + c²)

= (a + c)[(b + c)² – (b + c)c + c²]

= (a + c)(b² + 2bc + c² – c² – bc + c²)

= (a + c)(b² + bc + c²)

Từ đó ta có

Đáp án cần chọn là: A

Lời giải

Ta có (a + b + c)² + 12 = 4(a + b + c) + 2(ab + bc + ca)

⇔ a² + b² + c² + 2(ab + bc + ca) + 12 = 4(a + b + c) + 2(ab + ac + bc)

⇔ a² + b² + c² – 4a – 4b – 4c + 12 = 0

⇔ (a² – 4a + 4) + (b² – 4b + 4) + (c² – 4c + 4) = 0

⇔ (a – 2)² + (b – 2)² + (c – 2)² = 0

Mà (a – 2)² ≥ 0; (b – 2)² ≥ 0; (c – 2)² ≥ 0 với mọi a, b, c

Dấu “=” xảy ra

Đáp án cần chọn là: D