30 Bài tập trắc nghiệm Toán 10 Chương 8 (có lời giải) - Chân trời sáng tạo
haylamdo biên soạn và sưu tầm 50 bài tập trắc nghiệm tổng hợp Toán 10 Chương 8: Đại số tổ hợp có đáp án và lời giải chi tiết đầy đủ các mức độ sách Chân trời sáng tạo sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
30 Bài tập trắc nghiệm Toán 10 Chương 8 (có lời giải) - Chân trời sáng tạo
Câu 1. Tìm số hạng chứa x4 trong khai triển biết
A. –20;
B. 10;
C. –10;
D. 20.
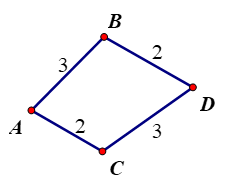
Câu 2.Từ thành phố A đến thành phố B có 3 con đường, từ thành phố A đến thành phố C có 2 con đường, từ thành phố B đến thành phố D có 2 con đường, từ thành phố C đến thành phố D có 3 con đường, không có con đường nào nối từ thành phố C đến thành phố B. Hỏi có bao nhiêu con đường đi từ thành phố A đến thành phố D.
A. 6;
B. 12;
C. 18;
D. 36.
Câu 3. Cho các số 1; 2; 3; 4; 5 có thể lập được bao nhiêu số tự nhiên lẻ gồm 3 chữ số đôi một khác nhau và chia hết cho 3.
A. 5120;
B. 3523;
C. 2520;
D. 3145.
Câu 4. Có 10 quả cầu đỏ được đánh số từ 1 đến 10, 7 quả cầu xanh được đánh số từ 1 đến 7 và 8 quả cầu vàng được đánh số từ 1 đến 8. Hỏi có bao nhiêu cách lấy ra 3 quả cầu khác màu và khác số.
A. 392;
B. 1023;
C. 3014;
D. 391.
Câu 5. Lớp 10A có 15 học sinh nam và 25 học sinh nữ. Thầy giáo có bao nhiêu cách chọn ra một học sinh nam và một học sinh nữ để thi đấu cầu lông đôi nam nữ.
A. 15;
B. 25;
C. 40;
D. 375.
Câu 6. Trong khai triển nhị thức (x + 2y)3 có bao nhiêu số hạng
A. 7;
B. 6;
C. 5;
D. 4.
Câu 7. Trong một hộp có 7 viên bi đỏ, 5 viên bi trắng và 6 viên bi xanh. Chọn ngẫu nhiên ra 4 viên bi. Có bao nhiêu cách để chọn được 2 viên bi xanh.
A. 315;
B. 525;
C. 150;
D. 990.
Câu 8.Nếu một đa giác đều có 44 đường chéo, thì số cạnh của đa giác là:
A. 11;
B. 10;
C. 9;
D. 8.
Câu 9.Một tổ gồm 7 nam và 6 nữ. Hỏi có bao nhiêu cách chọn 4 em đi trực sao cho có ít nhất 2 nữ?
A. 315;
B. 560;
C. 210;
D. 120.
Câu 10.Trong khai triển (x2 – 2x)5 hệ số của số hạng chứa x6 là:
A. –80;
B. –50;
C. 50;
D. 80.
Câu 11. Biết giá trị của n thoả mãn tính giá trị của biểu thức P =
A. P = 153;
B. P = 357;
C. P = 126;
D. P = 3402.
Câu 12.An muốn qua nhà Bình để cùng Bình đến chơi nhà Cường. Từ nhà An đến nhà Bình có 4 con đường đi, từ nhà Bình đến nhà Cường có 6 con đường đi. Hỏi An có bao nhiêu cách chọn đường đi đến nhà Cường?
A.16;
B.10;
C.24;
D.36.
Câu 13.Biến n là số nguyên dương thỏa mãn . Hệ số của x5 trong khai triển (1 – 3x)n bằng
A. –243;
B. –81;
C. 243;
D. 81.
Câu 14. Từ các chữ số 0; 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên chẵn có ba chữ số khác nhau?
A. 210;
B. 105;
C. 168;
D. 145.
Câu 15. Bạn Dũng có 9 quyển truyện tranh khác nhau và 6 quyển tiểu thuyết khác nhau. Bạn Dũng có bao nhiêu cách chọn ra một quyển sách để đọc vào cuối tuần.
A. 9;
B. 6;
C. 54;
D. 15.
Câu 16. Hệ số của x3y3 trong khai triển nhị thức (1 + x)5(1 + y)5 là
A. 10;
B. 400;
C. 100;
D. 36.
Câu 17. Cho các số 0; 1; 2; 3; 4; 5; 6; 7 có thể lập được bao nhiêu số tự nhiên lẻ gồm 4 chữ số đôi một khác nhau
A. 300;
B. 261;
C. 235;
D. 720.
Câu 18.Trong khai triển (x – 2y)4 số hạng chứa x2y2 là:
A. 24;
B. – 24;
C. 35;
D. – 35.
Câu 19.Trong khai triển số hạng chứa x2 là:
A. 30x2;
B. 20x2;
C. 40x2;
D. 25x2.
Câu 20. Trong khai triển nhị thức hệ số của x3 là . Giá trị của n là
A. n = 2;
B. n = 3;
C. n = 4;
D. n = 5.
Câu 21.Biết hệ số của x3 trong khai triển của (1 – 3x)n là –270. Giá trị của n là
A. n = 5;
B. n = 8;
C. n = 6;
D. n = 7.
Câu 22. Có bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau trong đó chứa các chữ số 3, 4, 5 và chữ số 4 đứng cạnh chữ số 3 và chữ số 5?
A. 1470;
B. 750;
C. 2940;
D. 1500.
Câu 23.Một lớp học có 30 bạn học sinh trong đó có 3 cán sự lớp. Hỏi có bao nhiêu cách cử 4 bạn học sinh đi dự đại hội đoàn trường sao cho trong 4 học sinh đó có ít nhất 1 cán sự lớp.
A. 23345;
B. 9585;
C. 12455;
D. 9855.
Câu 24. Có 10 đội bóng thi đấu theo thể thức vòng tròn một lượt, thắng được 3 điểm, hòa 1 điểm, thua 0 điểm. Kết thúc giải đấu, tổng cộng số điểm của tất cả 10 đội là 130. Hỏi có bao nhiêu trận hòa ?
A.7;
B. 8;
C. 5;
D. 6.
Câu 25. Trong kho đèn trang trí đang còn 5 bóng đèn loại I, 7 bóng đèn loại II, các bóng đèn đều khác nhau về màu sắc và hình dáng. Lấy ra 5 bóng đèn bất kỳ. Hỏi có bao nhiêu khả năng xảy ra số bóng đèn loại I nhiều hơn số bóng đèn loại II?
A. 246;
B. 3480;
C. 245;
D. 3360.
Câu 26.Tính giá trị , biết rằng
A. M = 78;
B. M = 18;
C. M = 96;
D. M = 84.
Câu 27. Cho số tự nhiên n thỏa mãn . Giá trị của biểu thức là
A. 1353;
B. 1989;
C. 880;
D. 2821.
Câu 28. Cho tập A gồm n điểm phân biệt trên mặt phẳng sao cho không có 3 điểm nào thẳng hàng. Tìm n sao cho số tam giác có 3 đỉnh lấy từ 3 điểm thuộc A gấp đôi số đoạn thẳng được nối từ 2 điểm thuộc A.
A. n = 6;
B. n = 12;
C. n = 8;
D. n = 15.
Câu 29. Cho các chữ số 2, 3, 4, 5, 6, 7, 8, 9 số các số tự nhiên chẵn có 3 chữ số lập thành từ các chữ số đã cho là
A. 36;
B. 18;
C. 256;
D. 108;
Câu 30. Tính giá trị của biểu thức P = . Biết giá trị của n thoả mãn (n ∈ ℕ, n ≥ 2).
A. P = 24396;
B. P = 24408;
C. P = 23968;
D. P = 12528;
Câu 1:
Tìm số hạng chứa x4 trong khai triển \({\left( {{x^2} - \frac{1}{x}} \right)^n}\) biết \(A_n^2 - C_n^2 = 10\)
A. – 20;
B. 10;
C. – 10;
D. 20.
Câu 2:
Từ thành phố A đến thành phố B có 3 con đường, từ thành phố A đến thành phố C có 2 con đường, từ thành phố B đến thành phố D có 2 con đường, từ thành phố C đến thành phố D có 3 con đường, không có con đường nào nối từ thành phố C đến thành phố B. Hỏi có bao nhiêu con đường đi từ thành phố A đến thành phố D.
A. 6;
B. 12;
C. 18;
D. 36.
Câu 3:
Cho các số 1; 2; 3; 4; 5 có thể lập được bao nhiêu số tự nhiên lẻ gồm 3 chữ số đôi một khác nhau và chia hết cho 3.
A. 5120;
B. 3523;
C. 2520;
D. 3145.
Câu 4:
Có 10 quả cầu đỏ được đánh số từ 1 đến 10, 7 quả cầu xanh được đánh số từ 1 đến 7 và 8 quả cầu vàng được đánh số từ 1 đến 8. Hỏi có bao nhiêu cách lấy ra 3 quả cầu khác màu và khác số.
A. 392;
B. 1023;
C. 3014;
D. 391.
Câu 5:
A. 15;
B. 25;
C. 40;
D. 375.
Câu 6:
Trong khai triển nhị thức (x + 2y)3 có bao nhiêu số hạng
A. 7;
B. 6;
C. 5;
D. 4.
Câu 7:
Trong một hộp có 7 viên bi đỏ, 5 viên bi trắng và 6 viên bi xanh. Chọn ngẫu nhiên ra 4 viên bi. Có bao nhiêu cách để chọn được 2 viên bi xanh.
A. 315;
B. 525;
C. 150;
D. 990.
Câu 8:
Nếu một đa giác đều có 44 đường chéo, thì số cạnh của đa giác là:
A. 11;
B. 10;
C. 9;
D. 8.
Câu 9:
Một tổ gồm 7 nam và 6 nữ. Hỏi có bao nhiêu cách chọn 4 em đi trực sao cho có ít nhất 2 nữ?
A. 315;
B. 560;
C. 210;
D. 120.
Câu 10:
Trong khai triển (x2 – 2x)5 hệ số của số hạng chứa x6 là:
A. – 80;
B. – 50;
C. 50;
D. 80.
Câu 11:
Biết giá trị của n thoả mãn \[A_n^3 = 56n\] tính giá trị của biểu thức P = \(3n + C_{n + 2}^4\)
A. P = 153;
B. P = 357;
C. P = 126;
D. P = 3402.
Câu 12:
An muốn qua nhà Bình để cùng Bình đến chơi nhà Cường. Từ nhà An đến nhà Bình có 4 con đường đi, từ nhà Bình đến nhà Cường có 6 con đường đi. Hỏi An có bao nhiêu cách chọn đường đi đến nhà Cường?
A. 16;
B. 10;
C. 24;
D. 36.
Câu 13:
Biến n là số nguyên dương thỏa mãn \(A_n^3 + 2A_n^2 = 100\). Hệ số của x5 trong khai triển (1 – 3x)n bằng
A. – 243;
B. – 81;
C. 243;
D. 81.
Câu 14:
Từ các chữ số 0; 1; 2; 3; 4; 5; 6 có thể lập được bao nhiêu số tự nhiên chẵn có ba chữ số khác nhau?
A. 210;
B. 105;
C. 168;
D. 145.
Câu 15:
Bạn Dũng có 9 quyển truyện tranh khác nhau và 6 quyển tiểu thuyết khác nhau. Bạn Dũng có bao nhiêu cách chọn ra một quyển sách để đọc vào cuối tuần.
A. 9;
B. 6;
C. 54;
D. 15.
Câu 16:
Hệ số của x3y3 trong khai triển nhị thức (1 + x)5(1 + y)5 là
A. 10;
B. 400;
C. 100;
D. 36.
Câu 17:
Cho các số 0; 1; 2; 3; 4; 5; 6; 7 có thể lập được bao nhiêu số tự nhiên lẻ gồm 4 chữ số đôi một khác nhau
A. 300;
B. 261;
C. 235;
D. 720.
Câu 18:
Trong khai triển (x – 2y)4 số hạng chứa x2y2 là:
A. 24;
B. – 24;
C. 35;
D. – 35.
Câu 19:
Trong khai triển \[{\left( {x + \frac{8}{{{x^2}}}} \right)^5}\] số hạng chứa x2 là:
A. 30x2;
B. 20x2;
C. 40x2;
D. 25x2.
Câu 20:
Trong khai triển nhị thức \({\left( {2{x^2} + \frac{1}{x}} \right)^n}\) hệ số của x3 là \({2^2}C_n^1\) Giá trị của n là
A. n = 2;
B. n = 3;
C. n = 4;
D. n = 5.
Câu 21:
Biết hệ số của x3 trong khai triển của (1 – 3x)n là – 270. Giá trị của n là
A. n = 5;
B. n = 8;
C. n = 6;
D. n = 7.
Câu 22:
Có bao nhiêu số tự nhiên có 6 chữ số đôi một khác nhau trong đó chứa các chữ số 3, 4, 5 và chữ số 4 đứng cạnh chữ số 3 và chữ số 5?
A. 1470;
B. 750;
C. 2940;
D. 1500.
Câu 23:
Một lớp học có 30 bạn học sinh trong đó có 3 cán sự lớp. Hỏi có bao nhiêu cách cử 4 bạn học sinh đi dự đại hội đoàn trường sao cho trong 4 học sinh đó có ít nhất 1 cán sự lớp.
A. 23345;
B. 9585;
C. 12455;
D. 9855.
Câu 24:
Có 10 đội bóng thi đấu theo thể thức vòng tròn một lượt, thắng được 3 điểm, hòa 1 điểm, thua 0 điểm. Kết thúc giải đấu, tổng cộng số điểm của tất cả 10 đội là 130. Hỏi có bao nhiêu trận hòa ?
A. 7;
B. 8;
C. 5;
D. 6.
Câu 25:
Trong kho đèn trang trí đang còn 5 bóng đèn loại I, 7 bóng đèn loại II, các bóng đèn đều khác nhau về màu sắc và hình dáng. Lấy ra 5 bóng đèn bất kỳ. Hỏi có bao nhiêu khả năng xảy ra số bóng đèn loại I nhiều hơn số bóng đèn loại II?
A. 246;
B. 3480;
C. 245;
D. 3360.
Câu 26:
Tính giá trị \[M = A_{n - 15}^2 + 3A_{n - 14}^3\], biết rằng \[C_n^4 = 20C_n^2\]
A. M = 78;
B. M = 18;
C. M = 96;
D. M = 84.
Câu 27:
Cho số tự nhiên n thỏa mãn \(3C_{n + 1}^3 - 3A_n^2 = 42\left( {n - 1} \right)\). Giá trị của biểu thức \(3C_n^4 - A_n^2\) là
A. 1353;
B. 1989;
C. 880;
D. 2821.
Câu 28:
Cho tập A gồm n điểm phân biệt trên mặt phẳng sao cho không có 3 điểm nào thẳng hàng. Tìm n sao cho số tam giác có 3 đỉnh lấy từ 3 điểm thuộc A gấp đôi số đoạn thẳng được nối từ 2 điểm thuộc A.
A. n = 6;
B. n = 12;
C. n = 8;
D. n = 15.
Câu 29:
Cho các chữ số 2, 3, 4, 5, 6, 7, 8, 9 số các số tự nhiên chẵn có 3 chữ số lập thành từ các chữ số đã cho là
A. 36;
B. 18;
C. 256;
D. 108;
Câu 30:
Tính giá trị của biểu thức P = \(3C_n^3 + 2A_n^4 - 2n\). Biết giá trị của n thoả mãn \[A_n^2 - C_{n + 1}^{n - 1} = 4n + 6\] (n \( \in \)ℕ, n ≥ 2).
A. P = 24396;
B. P = 24408;
C. P = 23968;
D. P = 12528;
Câu 1:
Giả sử một công việc có thể được thực hiện theo một trong ba phương án. Phương án A có 3 cách thực hiện, phương án B có 4 cách thực hiện, phương án C có 7 cách thực hiện (các cách thực hiện của cả ba phương án là khác nhau đôi một). Số cách thực hiện công việc đó là:
A. 14 cách;
B. 19 cách;
C. 84 cách;
Câu 2:
Giả sử một công việc được chia thành ba công đoạn. Công đoạn A có 8 cách thực hiện; ứng với mỗi cách đó có 3 cách thực hiện công đoạn B; ứng với mỗi cách thực hiện công đoạn A và mỗi cách thực hiện công đoạn B có 6 cách thực hiện công đoạn C. Khi đó số cách thực hiện công việc đã cho là:
A. 17 cách;
B. 26 cách;
C. 30 cách;
Câu 3:
Cho tập hợp A có n phần tử (n ≥ 1) và số nguyên k (1 ≤ k ≤ n). Phát biểu nào sau đây sai?
A. Một chỉnh hợp chập k của n phần tử trên là mỗi cách lấy k phần tử của tập A và sắp xếp chúng theo một thứ tự;
B. Một hoán vị của tập A là mỗi cách sắp xếp n phần tử của tập A theo một thứ tự;
C. Một tổ hợp chập k của n phần tử là mỗi cách lấy k phần tử của A;
Câu 4:
Cho n ≥ 1, n ∈ ℤ và 1 ≤ k ≤ n. Phát biểu nào sau đây sai?
A. P0 = 1;
B. ;
Câu 5:
Cho tập hợp X gồm n phần tử (n ≥ 1) và số nguyên k (1 ≤ k ≤ n). Một chỉnh hợp chập k của n phần tử là:
A. Một kết quả bất kì của sự sắp xếp k phần tử bất kì của tập hợp X;
B. Một kết quả của việc lấy k phần tử từ n phần tử của tập X và sắp xếp chúng theo một thứ tự nào đó;
C. Một số được tính bởi công thức: n(n – 1)(n – 2)…(n – k + 1);
Câu 7:
Tổng số mũ của a và b trong mỗi hạng tử khi khai triển biểu thức (m + 2n)5 bằng
A. 4;
B. 5;
C. 6;
Câu 1:
Từ các chữ số 1; 5; 6; 7; 9 có thể lập được bao nhiêu số tự nhiên có 4 chữ số?
A. 3 125;
B. 120;
C. 20;
Câu 2:
Trên bàn có 8 cây bút chì khác nhau, 6 cây bút bi khác nhau và 10 cuốn tập khác nhau. Một học sinh muốn chọn một đồ vật duy nhất (một cây bút chì hoặc một cây bút bi hoặc một cuốn tập) thì số cách chọn khác nhau là:
A. 24;
B. 480;
C. 48;
Câu 3:
Hội đồng quản trị của công ty X gồm 10 người. Hỏi có bao nhiêu cách bầu ra ba người vào ba vị trí chủ tịch, phó chủ tịch và thư kí, biết khả năng mỗi người là như nhau.
A. 1 000;
B. 720;
C. 30;
Câu 4:
Từ các chữ số 0; 1; 2; 3; 4; 5, có thể lập được bao nhiêu số lẻ gồm 4 chữ số khác nhau?
A. 154;
B. 145;
C. 144;
Câu 5:
Một mạng đường giao thông nối các tỉnh A, B, C, D, E, F và G như hình vẽ, trong đó chữ số được viết trên mỗi cạnh là số con đường có thể đi từ tỉnh này đến tỉnh kia, chẳng hạn chữ số 2 viết trên cạnh AB có nghĩa là có 2 con đường nối A và B,...
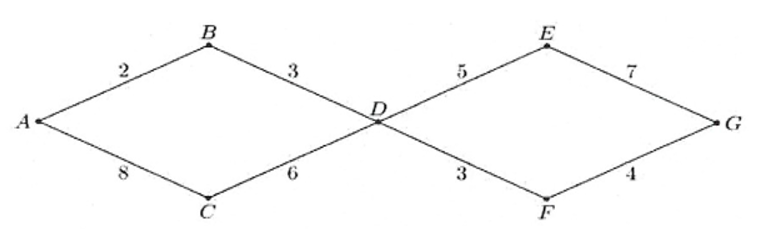
Số con đường từ A đến G là:
A. 101;
B. 2 538;
C. 38;
Câu 6:
Có ba môn thi Toán, Vật lí, Hóa học cần xếp vào 3 buổi thi, mỗi buổi một môn sao cho môn Toán không thi buổi đầu thì số cách xếp là:
A. 6;
B. 2;
C. 4;
Câu 7:
Có bao nhiêu cách chọn và sắp xếp thứ tự 5 cầu thủ để đá luân lưu, biết rằng cả 11 cầu thủ đều có khả năng như nhau?
A. 55 440;
B. 20 680;
C. 32 456;
Câu 8:
Trong một bình đựng 4 viên bi đỏ và 3 viên bi xanh. Lấy ngẫu nhiên 2 viên bi. Có bao nhiêu cách lấy được 2 viên bi cùng màu?
A. 18;
B. 9;
C. 22;
Câu 9:
Trong một trường có 4 học sinh giỏi lớp 12, 3 học sinh giỏi lớp 11 và 5 học sinh giỏi lớp 10. Cần chọn 5 học sinh giỏi để tham gia một cuộc thi với các trường khác sao cho khối 12 có 3 em và mỗi khối 10, 11 có đúng 1 em. Vậy số tất cả các cách chọn là:
A. 60;
B. 180;
C. 330;
Câu 11:
Số hạng không chứa x trong khai triển (x ≠ 0) (theo chiều số mũ của x giảm dần) là số hạng thứ:
A. 3;
B. 6;
C. 4;
Câu 12:
Cho x là số thực dương. Khai triển nhị thức , ta có hệ số của số hạng chứa xm bằng 6. Giá trị của m là:
A. m = 6;
B. m = 8;
C. m = 2;
Câu 14:
Biết rằng trong khai triển (với x ≠ 0), hệ số của số hạng chứa là 640. Khi đó giá trị của a bằng:
A. a = 4;
B. a = –4;
C. n ∈ {–4; 4};
Câu 15:
Giá trị n nguyên dương thỏa mãn là:
A. n = –2;
B. n = 5;
C. n ∈ {–2; 5};
Câu 2:
Cho tập hợp A = {0; 1; 2; 3; 4; 5; 6; 7}. Hỏi từ tập A có thể lập được bao nhiêu số tự nhiên gồm 5 chữ số đôi một khác nhau sao cho một trong 3 chữ số đầu tiên có chữ số 1?
A. 2 802;
B. 65;
C. 2 520;
Câu 3:
Từ các chữ số 0; 1; 2; 3; 4; 5, có thể lập được bao nhiêu số tự nhiên có 3 chữ số khác nhau và chia hết cho 9?
A. 16;
B. 18;
C. 20;
Câu 4:
Một hội đồng gồm 5 nam và 4 nữ được bầu vào một ban quản trị gồm 4 người. Biết rằng ban quản trị có ít nhất một nam và một nữ. Số cách bầu chọn là:
A. 240;
B. 260;
C. 126;
Câu 6:
Hệ số của số hạng x10 trong khai triển (1 + x + x2 + x3)5 là:
A. 5;
B. 50;
C. 101;