30 Bài tập trắc nghiệm Toán 10 Chương 9 (có lời giải) - Chân trời sáng tạo
haylamdo biên soạn và sưu tầm 50 bài tập trắc nghiệm tổng hợp Toán 10 Chương 9: Phương pháp toạ độ trong mặt phẳng có đáp án và lời giải chi tiết đầy đủ các mức độ sách Chân trời sáng tạo sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
30 Bài tập trắc nghiệm Toán 10 Chương 9 (có lời giải) - Chân trời sáng tạo
Câu 1. Trong mặt phẳng Oxy, cho ∆ABC có A(–4; 1), B(2; 4), C(2; –2). Tọa độ trọng tâm I của ∆ABC là:
A. I(1; 0);
B. I(0; 1);
C. I(–1; 0);
D. I(0; –1).
Câu 2. Cho và . Tìm a để .
A. ;
B. ;
C. ;
D. .
Câu 3. Trong mặt phẳng Oxy, cho ba điểm A(–1; 1), B(1; 3), C(5; 2). Tọa độ điểm D là đỉnh thứ tư của hình bình hành ABCD là:
A. (3; –2);
B. (5; 0);
C. (3; 0);
D. (5; –2).
Câu 4.Cho hai điểm A(6; –1) và B(x; 9). Giá trị của x để khoảng cách giữa A và B bằng là:
A. x ∈ ∅;
B. x = 1;
C. x = 11;
D. x = 11 hoặc x = 1.
Câu 5. Cho , . Góc giữa hai vectơ và bằng
A. 45°;
B. 60°;
C. 90°;
D. 135°.
Câu 6. Trong mặt phẳng Oxy, cho ∆ABC có A(–3; 0), B(3; 0) và C(2; 6). Gọi H(a; b) là trực tâm của ∆ABC. Giá trị của a + 6b bằng:
A. 3;
B. 6;
C. 7;
D. 5.
Câu 7. Trong mặt phẳng với hệ tọa độ Oxy, cho ∆ABC có A(3; 5), B(9; 7), C(11; –1). Gọi M, N lần lượt là trung điểm của AB và AC. Tọa độ của là:
A. (2; –8);
B. (1; –4);
C. (10; 6);
D. (5; 3).
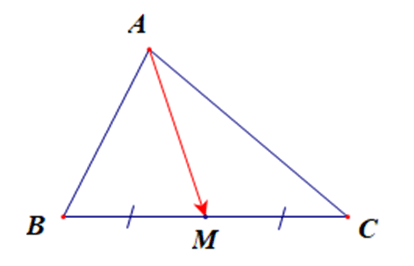
Câu 8. Cho ∆ABC có A(2; –1), B(4; 5), C(–3; 2). Phương trình tổng quát của đường trung tuyến AM là:
A. x + 3y – 7 = 0;
B. 3x + y – 7 = 0;
C. 3x + y – 5 = 0;
D. x + 3y – 5 = 0.
Câu 9. Giao điểm M của hai đường thẳng (d): và (d’): 3x – 2y – 1 = 0 là:
A. ;
B. ;
C. ;
D. .
Câu 10. Cặp đường thẳng nào sau đây vuông góc với nhau?
A. và d2: 2x + y – 1 = 0;
B. d1: x – 2 = 0 và ;
C. d1: 2x – y + 3 = 0 và d2: x – 2y + 1 = 0;
D. d1: 2x – y + 3 = 0 và d2: 4x – 2y + 1 = 0.
Câu 11. Cho đường thẳng (d): x – 2y + 5 = 0. Mệnh đề nào sau đây đúng?
A. (d) có hệ số góc ;
B. (d) cắt (d’): x – 2y = 0;
C. (d) đi qua A(1; –2);
D. (d) có phương trình tham số: .
Câu 12. Cho ∆ABC có C(–1; 2), đường cao BH: x – y + 2 = 0, đường phân giác trong AN: 2x – y + 5 = 0. Tọa độ điểm A là:
A. ;
B. ;
C. ;
D. .
Câu 13. Trong mặt phẳng Oxy, cho và . Tìm tọa độ sao cho .
A. ;
B. ;
C. ;
D. .
Câu 14. Trong mặt phẳng Oxy, cho hai điểm A(2; 4) và B(–2; 10). Giá trị k để điểm D(k; k + 1) thuộc đường thẳng AB là:
A. k = 2;
B. k = ;
C. k = 3;
D. k = .
Câu 15. Trong mặt phẳng Oxy, cho đường thẳng d: x + 2y – 3 = 0 và hai điểm A(–1; 2). B(2; 1). Điểm C thuộc đường thẳng d sao cho diện tích ∆ABC bằng 2. Tọa độ điểm C là:
A. C(–9; 6);
B. C(6; 9);
C. C(7; –2);
D. Cả A, C đều đúng.
Câu 16. Đường thẳng ∆ đi qua giao điểm của hai đường thẳng d1: 2x + y – 3 = 0 và d2: x – 2y + 1 = 0, đồng thời tạo với d3: y – 1 = 0 một góc Phương trình đường thẳng ∆ là:
A. 2x + y = 0; x – y – 1 = 0;
B. x + 2y = 0; x – 4y = 0;
C. x – y = 0; x + y – 2 = 0;
D. 2x + 1 = 0; x – 3y = 0.
Câu 17. Tọa độ tâm I và bán kính R của đường tròn (C): (x + 1)2 + y2 = 8 là:
A. I(–1; 0), R = 8;
B. I(–1; 0), R = 64;
C. I(–1; 0), R = ;
D. I(1; 0), R = .
Câu 18. Tọa độ tâm I và bán kính R của đường tròn (C): 2x2 + 2y2 – 8x + 4y – 1 = 0 là:
A. I(–2; 1), R = ;
B. I(2; –1), R = ;
C. I(4; –2), R = ;
D. I(–4; 2), R = .
Câu 19. Đường tròn (C) có tâm I(–2; 3) và đi qua điểm M(2; –3) có phương trình là:
A. (x + 2)2 + (y – 3)2 = ;
B. (x – 2)2 + (y + 3)2 = 52;
C. x2 + y2 + 4x – 6y – 57 = 0;
D. x2 + y2 + 4x – 6y – 39 = 0.
Câu 20. Cho phương trình x2 + y2 – 2mx – 4(m – 2)y + 6 – m = 0. Điều kiện của m để phương trình đã cho là một phương trình đường tròn là:
A. m ∈ ℝ;
B. ;
C. ;
D. .
Câu 21. Đường tròn (C) có tâm I thuộc đường thẳng d: x + 3y + 8 = 0, đi qua điểm A(–2; 1) và tiếp xúc với đường thẳng ∆: 3x – 4y + 10 = 0. Phương trình đường tròn (C) là:
A. (x – 2)2 + (y + 2)2 = 25;
B. (x + 5)2 + (y + 1)2 = 16;
C. (x + 2)2 + (y + 2)2 = 9;
D. (x – 1)2 + (y + 3)2 = 25.
Câu 22. Tọa độ tâm I của đường tròn đi qua ba điểm A(0; 4), B(2; 4), C(4; 0) là:
A. I(0; 0);
B. I(1; 0);
C. I(3; 2);
D. I(1; 1).
Câu 23. Cho đường tròn (C): x2 + y2 + 4x + 4y – 17 = 0, biết tiếp tuyến của (C) song song với đường thẳng d: 3x – 4y – 2023 = 0. Phương trình tiếp tuyến của đường tròn (C) là:
A. 3x – 4y + 23 = 0; 3x – 4y – 27 = 0;
B. 3x – 4y + 23 = 0; 3x – 4y + 27 = 0;
C. 3x – 4y – 23 = 0; 3x – 4y + 27 = 0;
D. 3x – 4y – 23 = 0; 3x – 4y – 27 = 0.
Câu 24.Cho đường tròn (C): (x – 2)2 + (y + 4)2 = 25, biết tiếp tuyến vuông góc với đường thẳng d: 3x – 4y + 5 = 0. Phương trình tiếp tuyến của (C) là:
A. 4x – 3y + 5 = 0; 4x – 3y – 45 = 0;
B. 4x + 3y + 5 = 0; 4x + 3y + 3 = 0;
C. 4x + 3y + 29 = 0;
D. 4x + 3y + 29 = 0; 4x + 3y – 21 = 0.
Câu 25. Cho đường tròn (C): x2 + y2 – 2x – 4y + 1 = 0. Gọi d1, d2 lần lượt là tiếp tuyến của đường tròn (C) tại điểm M(3; 2), N(1; 0). Tọa độ giao điểm của d1 và d2 là:
A. (3; 0);
B. (–3; 0);
C. (0; 3);
D. (0; –3).
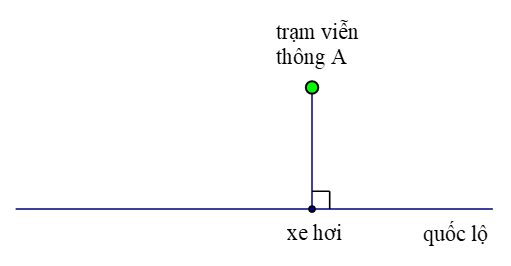
Câu 26.Một trạm viễn thông A được xây tại điểm có tọa độ (2; 3) (trong mặt phẳng Oxy). Một người đang ngồi trên xe hơi chạy trên đường quốc lộ có dạng một đường thẳng ∆ có phương trình x – 5y + 6 = 0.
Biết rằng mỗi đơn vị độ dài tương ứng với 1 km. Khoảng cách ngắn nhất giữa người đó và trạm viễn thông A bằng:
A. 2,5 km;
B. 0,2 km;
C. 1,37 km;
D. 0,5 km.
Câu 27. Cho M(x; y) nằm trên elip (E): . Tỉ số giữa tiêu cự và độ dài trục lớn bằng:
A. ;
B. ;
C. ;
D. .
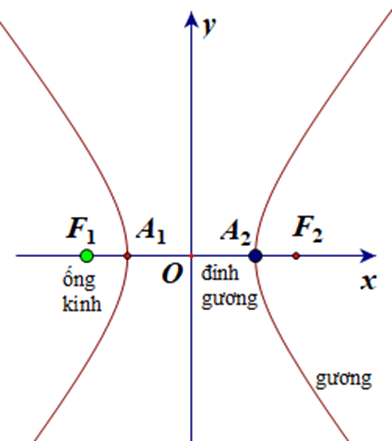
Câu 28. Một gương có mặt cắt là một hypebol có phương trình được dùng để chụp ảnh toàn cảnh. Máy ảnh hướng về phía đỉnh của gương và được đặt ở vị trí sao cho ống kính trùng với một tiêu điểm của gương như hình vẽ.
Biết rằng x, y được đo theo inch. Khoảng cách từ ống kính tới đỉnh gương bằng khoảng:
A. 24,6 inch;
B. 0,7 inch;
C. 12 inch;
D. 23,3 inch.
Câu 29.Một tòa tháp có mặt cắt hình hypebol có phương trình . Biết khoảng cách từ nóc tháp đến tâm đối xứng O của hypebol bằng khoảng cách từ tâm đối xứng O đến đáy tháp. Tòa tháp có chiều cao 50 m. Bán kính đáy của tháp bằng:
A. 43,28 m;
B. 22,25 m;
C. 28,31 m;
D. 57,91 m.
Câu 30. Một anten gương đơn hình parabol có phương trình y2 = 20x. Ống thu của anten được đặt tại tiêu điểm của nó. Ta sẽ đặt ống thu tại điểm có tọa độ là:
A. (0; 10);
B. (0; 5);
C. (10; 0);
D. (5; 0).
Câu 1:
Trong mặt phẳng Oxy, cho ∆ABC có A(–4; 1), B(2; 4), C(2; –2). Tọa độ trọng tâm I của ∆ABC là:
A. I(1; 0);
B. I(0; 1);
C. I(–1; 0);
D. I(0; –1).
Câu 3:
Trong mặt phẳng Oxy, cho ba điểm A(–1; 1), B(1; 3), C(5; 2). Tọa độ điểm D là đỉnh thứ tư của hình bình hành ABCD là:
A. (3; –2);
B. (5; 0);
C. (3; 0);
D. (5; –2).
Câu 4:
Cho hai điểm A(6; –1) và B(x; 9). Giá trị của x để khoảng cách giữa A và B bằng là:
A. x ∈ ∅;
B. x = 1;
C. x = 11;
D. x = 11 hoặc x = 1.
Câu 6:
Trong mặt phẳng Oxy, cho ∆ABC có A(–3; 0), B(3; 0) và C(2; 6). Gọi H(a; b) là trực tâm của ∆ABC. Giá trị của a + 6b bằng:
A. 3;
B. 6;
C. 7;
D. 5.
Câu 7:
Trong mặt phẳng với hệ tọa độ Oxy, cho ∆ABC có A(3; 5), B(9; 7), C(11; –1). Gọi M, N lần lượt là trung điểm của AB và AC. Tọa độ của là:
A. (2; –8);
B. (1; –4);
C. (10; 6);
D. (5; 3).
Câu 8:
Cho ∆ABC có A(2; –1), B(4; 5), C(–3; 2). Phương trình tổng quát của đường trung tuyến AM là:
A. x + 3y – 7 = 0;
B. 3x + y – 7 = 0;
C. 3x + y – 5 = 0;
D. x + 3y – 5 = 0.
Câu 10:
Cặp đường thẳng nào sau đây vuông góc với nhau?
A. và d2: 2x + y – 1 = 0;
B. d1: x – 2 = 0 và
C. d1: 2x – y + 3 = 0 và d2: x – 2y + 1 = 0;
D. d1: 2x – y + 3 = 0 và d2: 4x – 2y + 1 = 0.
Câu 11:
Cho đường thẳng (d): x – 2y + 5 = 0. Mệnh đề nào sau đây đúng?
A. (d) có hệ số góc k = 1/2;
B. (d) cắt (d’): x – 2y = 0;
C. (d) đi qua A(1; –2);
D. (d) có phương trình tham số: .
Câu 12:
Cho ∆ABC có C(–1; 2), đường cao BH: x – y + 2 = 0, đường phân giác trong AN: 2x – y + 5 = 0. Tọa độ điểm A là:
A.
B.
C.
D.
Câu 14:
Trong mặt phẳng Oxy, cho hai điểm A(2; 4) và B(–2; 10). Giá trị k để điểm D(k; k + 1) thuộc đường thẳng AB là:
A. k = 2;
B. k = 7/5
C. k = 3;
D. k = 12/5
Câu 15:
Trong mặt phẳng Oxy, cho đường thẳng d: x + 2y – 3 = 0 và hai điểm A(–1; 2). B(2; 1). Điểm C thuộc đường thẳng d sao cho diện tích ∆ABC bằng 2. Tọa độ điểm C là:
A. C(–9; 6);
B. C(6; 9);
C. C(7; –2);
D. Cả A, C đều đúng.
Câu 16:
Đường thẳng ∆ đi qua giao điểm của hai đường thẳng d1: 2x + y – 3 = 0 và d2: x – 2y + 1 = 0, đồng thời tạo với d3: y – 1 = 0 một góc Phương trình đường thẳng ∆ là:
A. 2x + y = 0; x – y – 1 = 0;
B. x + 2y = 0; x – 4y = 0;
C. x – y = 0; x + y – 2 = 0;
D. 2x + 1 = 0; x – 3y = 0.
Câu 17:
Tọa độ tâm I và bán kính R của đường tròn (C): (x + 1)2 + y2 = 8 là:
A. I(–1; 0), R = 8;
B. I(–1; 0), R = 64;
C. I(–1; 0), R = ;
D. I(1; 0), R = .
Câu 18:
Tọa độ tâm I và bán kính R của đường tròn (C): 2x2 + 2y2 – 8x + 4y – 1 = 0 là:
A. I(–2; 1), R = ;
B. I(2; –1), R = ;
C. I(4; –2), R = ;
D. I(–4; 2), R = .
Câu 19:
Đường tròn (C) có tâm I(–2; 3) và đi qua điểm M(2; –3) có phương trình là:
A. (x + 2)2 + (y – 3)2 = ;
B. (x – 2)2 + (y + 3)2 = 52;
C. x2 + y2 + 4x – 6y – 57 = 0;
D. x2 + y2 + 4x – 6y – 39 = 0.
Câu 20:
Cho phương trình x2 + y2 – 2mx – 4(m – 2)y + 6 – m = 0. Điều kiện của m để phương trình đã cho là một phương trình đường tròn là:
A. m ∈ ℝ;
B.
C.
D.
Câu 21:
Đường tròn (C) có tâm I thuộc đường thẳng d: x + 3y + 8 = 0, đi qua điểm A(–2; 1) và tiếp xúc với đường thẳng ∆: 3x – 4y + 10 = 0. Phương trình đường tròn (C) là:
A. (x – 2)2 + (y + 2)2 = 25;
B. (x + 5)2 + (y + 1)2 = 16;
C. (x + 2)2 + (y + 2)2 = 9;
D. (x – 1)2 + (y + 3)2 = 25.
Câu 22:
Tọa độ tâm I của đường tròn đi qua ba điểm A(0; 4), B(2; 4), C(4; 0) là:
A. I(0; 0);
B. I(1; 0);
C. I(3; 2);
D. I(1; 1).
Câu 23:
Cho đường tròn (C): x2 + y2 + 4x + 4y – 17 = 0, biết tiếp tuyến của (C) song song với đường thẳng d: 3x – 4y – 2023 = 0. Phương trình tiếp tuyến của đường tròn (C) là:
A. 3x – 4y + 23 = 0; 3x – 4y – 27 = 0;
B. 3x – 4y + 23 = 0; 3x – 4y + 27 = 0;
C. 3x – 4y – 23 = 0; 3x – 4y + 27 = 0;
D. 3x – 4y – 23 = 0; 3x – 4y – 27 = 0.
Câu 24:
Cho đường tròn (C): (x – 2)2 + (y + 4)2 = 25, biết tiếp tuyến vuông góc với đường thẳng d: 3x – 4y + 5 = 0. Phương trình tiếp tuyến của (C) là:
A. 4x – 3y + 5 = 0; 4x – 3y – 45 = 0;
B. 4x + 3y + 5 = 0; 4x + 3y + 3 = 0;
C. 4x + 3y + 29 = 0;
D. 4x + 3y + 29 = 0; 4x + 3y – 21 = 0.
Câu 25:
Cho đường tròn (C): x2 + y2 – 2x – 4y + 1 = 0. Gọi d1, d2 lần lượt là tiếp tuyến của đường tròn (C) tại điểm M(3; 2), N(1; 0). Tọa độ giao điểm của d1 và d2 là:
A. (3; 0);
B. (–3; 0);
C. (0; 3);
D. (0; –3).
Câu 26:
Một trạm viễn thông A được xây tại điểm có tọa độ (2; 3) (trong mặt phẳng Oxy). Một người đang ngồi trên xe hơi chạy trên đường quốc lộ có dạng một đường thẳng ∆ có phương trình x – 5y + 6 = 0.
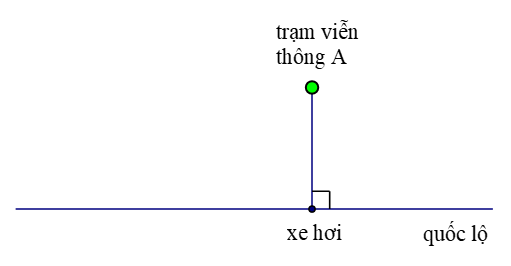
Biết rằng mỗi đơn vị độ dài tương ứng với 1 km. Khoảng cách ngắn nhất giữa người đó và trạm viễn thông A bằng:
A. 2,5 km;
B. 0,2 km;
C. 1,37 km;
D. 0,5 km.
Câu 27:
Cho M(x; y) nằm trên elip (E): . Tỉ số giữa tiêu cự và độ dài trục lớn bằng:
A.
B.
C.
D.
Câu 28:
Một gương có mặt cắt là một hypebol có phương trình được dùng để chụp ảnh toàn cảnh. Máy ảnh hướng về phía đỉnh của gương và được đặt ở vị trí sao cho ống kính trùng với một tiêu điểm của gương như hình vẽ.
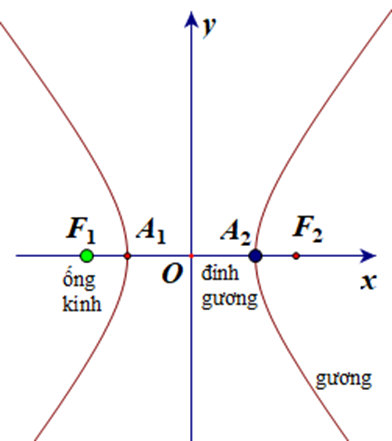
Biết rằng x, y được đo theo inch. Khoảng cách từ ống kính tới đỉnh gương bằng khoảng:
A. 24,6 inch;
B. 0,7 inch;
C. 12 inch;
D. 23,3 inch.
Câu 29:
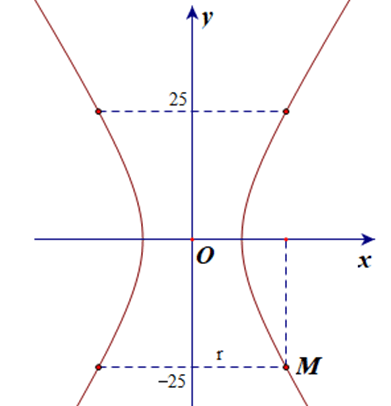
Một tòa tháp có mặt cắt hình hypebol có phương trình . Biết khoảng cách từ nóc tháp đến tâm đối xứng O của hypebol bằng khoảng cách từ tâm đối xứng O đến đáy tháp. Tòa tháp có chiều cao 50 m. Bán kính đáy của tháp bằng:
A. 43,28 m;
B. 22,25 m;
C. 28,31 m;
D. 57,91 m.
Câu 30:
Một anten gương đơn hình parabol có phương trình y2 = 20x. Ống thu của anten được đặt tại tiêu điểm của nó. Ta sẽ đặt ống thu tại điểm có tọa độ là:
A. (0; 10);
B. (0 ; 5);
C. (10; 0);
D. (5; 0).
Câu 1:
Trong mặt phẳng tọa độ Oxy cho 2 điểm A(2; 5) và B(6; 7). Tọa độ C là trung điểm của AB là
A. C = (4; 6);
B. C = (5; 6);
C. C = (4; 5);
Câu 2:
Trong mặt phẳng tọa độ Oxy cho ba điểm A(3; 6), B(6; 9) và C(9; 12). Tọa độ trọng tâm của tam giác ABC là
A. G(6; 6);
B. G(6; 9);
C. G(9; 12);
Câu 3:
Phương trình tổng quát của đường thẳng d đi qua điểm M(2; 2) và có vectơ pháp tuyến là:
A. x + 3y – 6 = 0;
B. 3x + y – 8 = 0;
C. x + 3y – 8 = 0;
Câu 4:
Chọn khẳng định đúng?
A. Vectơ chỉ phương của một đường thẳng luôn luôn song song với vectơ pháp tuyến của đường thẳng đó;
B. Vectơ chỉ phương của một đường thẳng luôn luôn vuông góc với vectơ pháp tuyến của đường thẳng đó;
C. Vectơ chỉ phương của một đường thẳng luôn luôn vuông góc với đường thẳng đó;
Câu 5:
Tọa độ tâm I và bán kính R của đường tròn có phương trình: (x – 1)2 + (y – 10)2 = 81 lần lượt là:
A. I(1; 10) và R = 9;
B. I(–1; –10) và R = 9;
C. I(1; 10) và R = 81;
Câu 6:
Đường tròn (C): x2 + y2 – 2x – 6y – 15 = 0 có tâm và bán kính lần lượt là:
A. I(3; 1), R = 5;
B. I(1; 3), R = 5;
C. I(3; 1), R = 6;
Câu 7:
Chọn khẳng định đúng duy nhất trong các khẳng định sau?
A. Giao điểm của Hypebol với trục Ox gọi là các đỉnh;
B. Đoạn thẳng nối 2 đỉnh của Hypebol gọi là trục ảo;
C. Hypebol không có trục ảo;
Câu 8:
Chọn khẳng định đúng trong các khẳng định sau:
A. Đường tròn (C) có phương trình x2 + y2 = 3 có bán kính R = 3;
B. Elip (E) có hai tiêu điểm là F1(0; –1) và F2(0; 1);
C. Hypebol (H) có tiêu cự bằng 10;
Câu 1:
Trong mặt phẳng tọa độ Oxy cho và . Tọa độ của vectơ là:
A. (7; –12);
B. (7; 12);
C. (1; –12);
Câu 2:
Trong mặt phẳng tọa độ Oxy cho 2 điểm A(2; 4) và B(4; 5). Tọa độ điểm D thỏa mãn là:
A. D = (2; 3);
B. D = (6; 6);
C. D = (4; 6);
Câu 3:
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(2; 5), B(4; 2) và C(5; 1). Tọa độ điểm D thỏa mãn ABDC là hình bình hành là
A. D(2; 3);
B. D(1; 3);
C. D(7; ‒2);
Câu 4:
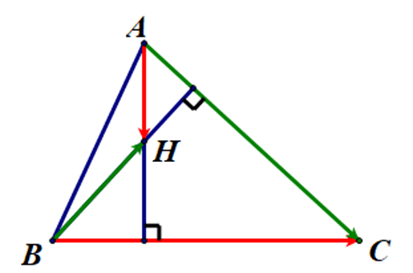
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(4; 3), B(2; 7) và C(– 3; –8). Tọa độ chân đường cao H kẻ từ A xuống cạnh BC là:
A. H(1; –4);
B. H(–1; 4);
C. H(1; 4);
Câu 5:
Trong hệ tọa độ Oxy cho điểm M(3; 4) và đường thẳng d có phương trình: x + 4y – 10 = 0. Khoảng cách nhỏ nhất từ điểm M đến một điểm bất kì nằm trên đường thẳng d bằng:
A.
B.
C.
D.
Câu 6:
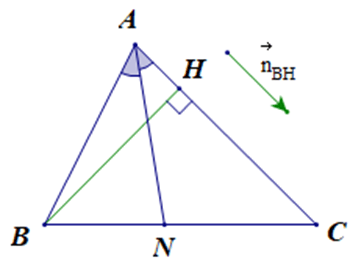
Trong mặt phẳng tọa độ Oxy, cho G là trọng tâm tam giác ABC. Tính góc giữa 2 đường thẳng AG và AC, biết A(1; 2), B(2; 5) và M(3; 4) là trung điểm của BC.
A. (AG, AC) 26o34’;
B. (AG, AC) 30o27’;
C. (AG, AC) 24o3’;
Câu 7:
Cho hai đường thẳng d: 7x + 2y – 1 = 0 và : .
Vị trí tương đối của hai đường thẳng là:
A. Trùng nhau;
B. Song song;
C. Vuông góc với nhau;
Câu 9:
Phương trình tiếp tuyến của đường tròn có phương trình: x2 + y2 – 2x – 4y + 4 = 0 tại điểm M nằm trên trục tung là:
A. x = 0 ;
B. x + 2y – 1 = 0;
C. 3x + 2y – 1 = 0;
Câu 10:
Viết phương trình đường tròn tâm I đi qua 3 điểm A(1; 1), B(2; 3) và C(4; 6).
A. x2 + y2 – 5x + y + 26 = 0;
B. x2 + y2 – 4x + 17y + 26 = 0;
C. x2 + y2 – 45x + 17y + 26 = 0;
Câu 11:
Viết phương trình đường tròn tâm I(1; 2) tiếp xúc với đường thẳng d: x + y – 2 = 0.
A. (x – 1)2 + (y – 2)2 = 4;
B. (x – 1)2 + (y – 2)2 = 2;
C. (x – 1)2 + (y – 2)2 = ;
Câu 12:
Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
A. x2 + y2 + 2x – 4y + 9 = 0;
B. x2 + y2 – 6x + 4y + 13 = 0;
C. 2x2 + 2y2 – 8x – 4y + 2 = 0;
Câu 13:
Phương trình chính tắc của Elip có trục lớn gấp đôi trục bé và đi qua điểm M(2; – 2) là:
A.
B.
C.
D.
Câu 14:
Viết phương trình chính tắc của Hypebol có độ dài trục thực là 8 và tiêu cự bằng 10.
A.
B.
C.
D.
Câu 15:
Cho một Parabol có tiêu điểm F. Viết phương trình chính tắc của Parabol đó biết F là trung điểm của AB và A(1; 0) và B(5; 0)
A. y2 = 1,5x;
B. y2 = 3x;
C. y2 = 6x
Câu 1:
Viết phương trình tham số của đường thẳng d đi qua M(2; 6) và song song với đường thẳng x + 3y – 10 = 0.
A.
B.
C.
D.
Câu 2:
Đường thẳng d tạo với đường thẳng : x + 2y – 6 = 0 một góc 45°. Hệ số góc k của đường thẳng d là:
A. k = hoặc k = – 3;
B. k = hoặc k = 3;
C. k = hoặc k = – 3;
Câu 3:
Cho phương trình x2 + y2 – 2(m + 1)x + 4y – 1 = 0 (1). Với giá trị nào của m thì (1) là phương trình đường tròn có bán kính nhỏ nhất?
A. m = 2;
B. m = – 1;
C. m = 1;
Câu 4:
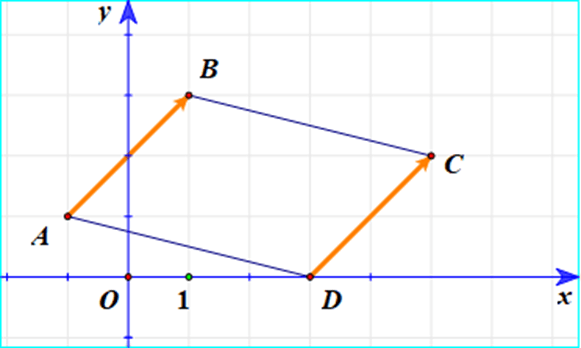
Hai con tàu cùng rời cảng và đi theo hai hướng khác nhau. Chọn hệ trục tọa độ sao cho bến cảng là gốc tọa độ. Khi đó quãng đường đi được và hướng của tàu thứ nhất và thứ hai được biểu thị bởi hai vectơ như hình dưới đây (độ dài một đơn vị trên trục tương ứng với 100 m trên thực tế).
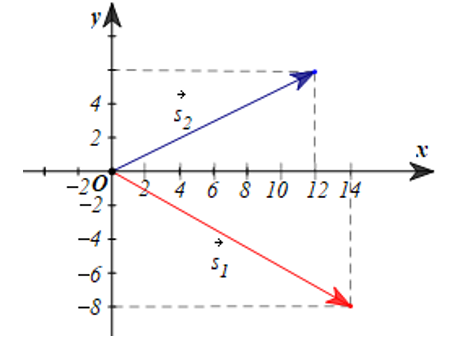
Hỏi quãng đường tàu thứ nhất đi được dài hơn tàu thứ hai bao nhiêu mét? Khoảng cách giữa hai tàu là bao nhiêu mét? (kết quả làm tròn đến hàng phần trăm).
A. 347,54 m và 1 216,55 m;
B. 1 216,55 m và 347,50 m;
C. 347,54 m và 2 877,36 m;
Câu 5:
Một tòa tháp có mặt cắt hình hypebol có phương trình . Biết khoảng cách từ nóc tháp đến tâm đối xứng O của hypebol bằng khoảng cách từ tâm đối xứng O đến đáy tháp. Tòa tháp có chiều cao 50 m. Bán kính đáy của tháp khoảng:
A. 43,28 m;
B. 22,25 m;
C. 28,31 m;
Câu 6:
Một cổng của một trường đại học hình Parabol cao 20 m và bề rộng của cổng tại chân cổng là 20 m. Bề rộng của cổng tại chỗ cách đỉnh cổng 4 m là:

A. m;
B. 2 m;
C. 4 m;
Câu 7:
Cho hình vẽ sau:
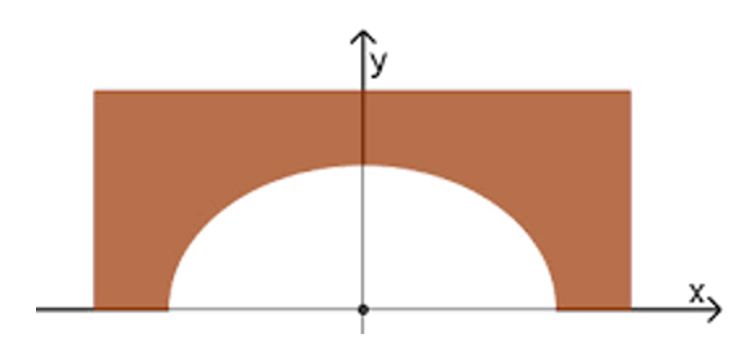
Một cổng hầm hình Elip có dạng như hình trên. Chiều cao của cả hầm là 10 m, chiều rộng là 20 m. Mỗi bên tường dày 2 m và tính từ đỉnh cổng hầm đến đỉnh hầm là 4 m. Phương trình chính tắc của Elip trên là:
A.
B.
C.
D.