30 Bài tập trắc nghiệm Toán 10 Chương 10 (có lời giải) - Chân trời sáng tạo
haylamdo biên soạn và sưu tầm 50 bài tập trắc nghiệm tổng hợp Toán 10 Chương 10: Xác suất có đáp án và lời giải chi tiết đầy đủ các mức độ sách Chân trời sáng tạo sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
30 Bài tập trắc nghiệm Toán 10 Chương 10 (có lời giải) - Chân trời sáng tạo
Câu 1. Chọn khẳng định sai trong các khẳng định sau:
A. Phép thử ngẫu nhiên (gọi tắt là phép thử) là một hoạt động mà ta không thể biết trước được kết quả của nó;
B. Tập hợp tất cả các kết quả có thể có của phép thử ngẫu nhiên được gọi là không gian mẫu;
C. Với mọi biến cố A, 0 ≤ P(A) ≤ 1;
D. Xác suất của mỗi biến cố đo lường xảy ra của biến cố đó. Biến cố có khả năng xảy ra càng cao thì xác suất của nó càng xa 1.
Câu 2. Xúc xắc có 6 mặt đánh số chấm từ 1 đến 6 chấm. Không gian mẫu của 1 lần tung xúc xắc là:
A. Ω = {1; 2; 3; 4; 5; 6};
B. Ω = 1; 2; 3; 4; 5; 6;
C. Ω = {1}; {2}; {3}; {4}; {5}; {6};
D. Ω = ∅.
Câu 3. Tung xúc xắc 5 lần sẽ có không gian mẫu gồm bao nhiêu cách xuất hiện mặt của xúc xắc?
A. 6!;
B. 30;
C. 65;
D. vô số.
Câu 4. Chọn khẳng định đúng trong các khẳng định sau:
A. Phép thử ngẫu nhiên (gọi tắt là phép thử) là một hoạt động mà ta không thể biết trước được kết quả của nó;
B. Cho A là một biến cố. Khi đó biến cố “Không xảy ra A”, kí hiệu là , được gọi là biến cố đối của A;
C. P(Ω) = 1, P(∅) = 0;
D. Cả A, B, C đều đúng.
Câu 5. Một ban đại diện gồm 5 người được thành lập từ 10 người có tên sau đây: Lan, Mai, Minh, Thu, Miên, An, Hà, Thanh, Mơ, Nga. Tính xác xuất để ít nhất 3 người trong ban đại diện có tên bắt đầu bằng chữ M.
A. ;
B. ;
C. ;
D. .
Câu 6. Một hộp chứa 18 quả cầu gồm 8 quả cầu màu xanh và 10 quả cầu màu trắng. Chọn ngẫu nhiên 2 quả từ hộp đó. Xác xuất để chọn được 2 quả cầu cùng màu là:
A. ;
B. ;
C. ;
D. .
Câu 7. Điền tiếp vào chỗ trống: “Giả sử một phép thử có không gian mẫu gồm …. các kết quả có cùng khả năng xảy ra và A là một biến cố. Xác suất của biến cố A là một số, kí hiệu là P(A), được xác định bởi công thức:
P(A) =
trong đó n(A) và n(Ω) lần lượt là kí hiệu số phần tử của tập A và Ω”.
A. vô hạn;
B. hữu hạn;
C. tất cả;
D. vô số.
Câu 8. Trên bàn có 5 quả táo và 5 quả cam. Xác định số phần tử không gian mẫu của phép thử lấy 3 quả ở trên bàn sau đó bỏ ra ngoài lấy tiếp 2 quả nữa.
A. 2 520 phần tử;
B. 5 220 phần tử;
C. 1 050 phần tử;
D. 2 150 phần tử.
Câu 9. Cho tập hợp A gồm các số nguyên dương nhỏ hơn hoặc bằng 40. Chọn 2 phần tử trong tập hợp A. Gọi B là biến cố “Phần tử được chọn chia hết cho 5”. Số kết quả thuận lợi cho biến cố B là:
A. 26;
B. 27;
C. 25;
D. 28.
Câu 10. Từ các chữ số {1; 2; 3; 4; 5; 6}, lập một số bất kì gồm 3 chữ số. Xác suất để số nhận được chia hết cho 6 là:
A. ;
B. ;
C. ;
D. .
Câu 11. Hai người ngang tài ngang sức tranh chức vô địch của một cuộc thi cờ vua. Người dành chiến thắng là người đầu tiên thắng được 5 ván cờ. Tại thời điểm người chơi thứ nhất đã thắng 4 ván và người chơi thứ hai mới thắng 2 ván (không có ván nào hòa). Xác suất để người chơi thứ nhất dành chiến thắng là:
A. ;
B. ;
C. ;
D. .
Câu 12. Một người bỏ ngẫu nhiên 4 lá thư vào 4 bì thư đã được ghi sẵn địa chỉ cần gửi. Xác xuất để có ít nhất 1 lá thư bỏ đúng phong bì của nó là:
A. ;
B. ;
C. ;
D. Không xác định.
Câu 13. Một tổ có 7 học sinh nam và 3 học sinh nữ. Cô giáo chọn ngẫu nhiên 2 bạn trong tổ lên kiểm tra bài cũ. Xác suất để 2 bạn chọn lên là 2 bạn nữ là:
A. ;
B. ;
C. ;
D. .
Câu 14. Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên:
A. Gieo đồng tiền xem xuất hiện mặt ngửa hay mặt sấp;
B. Gieo 3 đồng tiền và xem có mấy đồng tiền lật ngửa;
C. Chọn bất kì 1 học sinh trong lớp và xem là nam hay nữ;
D. Bỏ hai viên bi xanh và ba viên bi đỏ trong một chiếc hộp, sau đó lấy từng viên một để đếm xem có tất cả bao nhiêu viên bi.
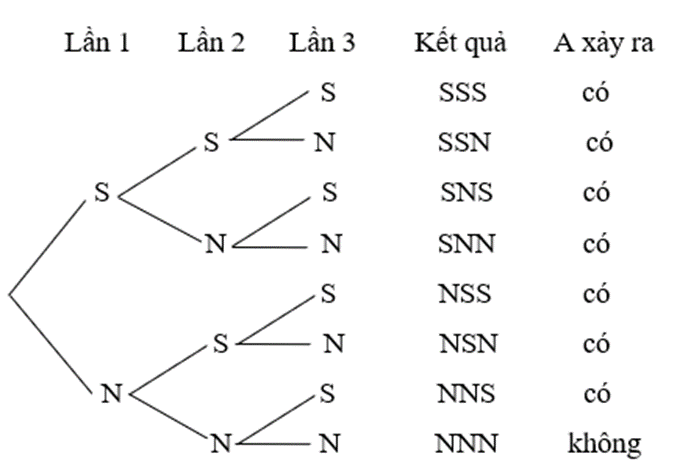
Câu 15. Gieo hai đồng tiền một lần. Kí hiệu S, N lầm lượt để chỉ đồng tiền lật sấp, lật ngửa. Xác định biến cố M: “Hai đồng tiền xuất hiện hai mặt không giống nhau”.
A. M = {NN, SS};
B. M = {NS, SN};
C. M = {NS, NN};
D. M = {SS, SN}.
Câu 16. Một hộp có:
• 2 viên bi trắng được đánh số từ 1 đến 2;
• 3 viên bi xanh được đánh số từ 3 đến 5;
• 2 viên bi đỏ được đánh số từ 6 đến 7.
Lấy ngẫu nhiên hai viên bi, mô tả không gian mẫu nào dưới đây là đúng?
A. Ω = {(m, n)| 1 ≤ m ≤ 7, 1 ≤ n ≤ 7};
B. Ω = {(m, n)| 1 ≤ m ≤ 5, 6 ≤ n ≤ 7};
C. Ω = {(m, n)| 1 ≤ m ≤ 7, 1 ≤ n ≤ 7, m ≠ n};
D. Ω = {(m, n)| 1 ≤ m ≤ 3, 4 ≤ n ≤ 7}.
Câu 17. Cho tập hợp A gồm các số nguyên dương nhỏ hơn hoặc bằng 60. Chọn 1 phần tử trong tập hợp A. Gọi B là biến cố “Phần tử được chọn chia hết cho 10”. Số kết quả thuận lợi cho biến cố B là:
A. 6;
B. 7;
C. 5;
D. 9.
Câu 18. Trên bàn có 3 quả táo và 4 quả cam. Xác định số phần tử không gian mẫu của phép thử lấy 2 quả ở trên bàn sau đó bỏ ra ngoài rồi lấy tiếp 1 quả nữa.
A. 7 phần tử;
B. 5 phần tử;
C. 105 phần tử;
D. 21 phần tử.
Câu 19. Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Số kết quả thuận lợi cho biến cố B: “4 viên bi lấy ra có ít nhất một viên bi màu xanh” là:
A. 10 626;
B. 1 820;
C. 7 566;
D. 8 806.
Câu 20. Gieo một con xúc xắc. Xác suất để mặt chấm chẵn xuất hiện là?
A. 0,2;
B. 0,3;
C. 0,4;
D. 0,5.
Câu 21. Trong hộp có 3 viên bi xanh và 5 viên bi đỏ. Lấy ngẫu nhiên trong hộp 3 viên bi. Xác suất của biến cố A: “Lấy ra được 3 viên bi màu đỏ” là:
A. P(A) = ;
B. P(A) = ;
C. P(A) = ;
D. P(A) = .
Câu 22. Tung một đồng xu cân đối và đồng chất 3 lần liên tiếp. Xác suất của biến cố A: “Trong 3 lần tung có ít nhất 1 lần xuất hiện mặt sấp” là:
A. P(A) = ;
B. P(A) = ;
C. P(A) = ;
D. P(A) = .
Câu 23. Trong hộp có 6 quả cầu đỏ và 4 quả cầu xanh, lấy ngẫu nhiên đồng thời 4 quả cầu. Xác suất để 4 quả cầu lấy ra cùng màu là:
A. P =
B. P =
C. P =
D. P = .
Câu 24. Một cái túi chứa 3 viên bi đỏ và 5 bi xanh, 6 viên bi vàng. Chọn ngẫu nhiên 3 viên bi. Xác suất để 3 viên bi có cả ba màu đỏ, xanh, vàng là:
A. ;
B. ;
C. 1;
D. .
Câu 25. Lớp 11B có 20 học sinh gồm 12 nữ và 8 nam. Cần chọn ra 2 học sinh của lớp đi lao động. Xác suất để chọn được 2 học sinh trong đó có cả nam và nữ là:
A. ;
B. ;
C. ;
D. .
Câu 26. Gieo một con xúc xắc cân đối và đồng chất. Giả sử xúc xắc xuất hiện mặt b chấm. Xác suất để phương trình x2 + bx + 2 = 0 có hai nghiệm phân biệt là:
A. ;
B. ;
C. ;
D. .
Câu 27. Một hộp đựng 9 viên bi có kích thước và khối lượng như nhau, trong đó có 4 viên bi đỏ và 5 viên bi xanh. Lấy ngẫu nhiên từ hộp 3 viên bi. Xác suất để 3 viên bi lấy ra có ít nhất 2 viên bi màu xanh là:
A.
B.
C.
D.
Câu 28. Đội tuyển của một lớp có 8 học sinh nam và 4 học sinh nữ. Trong buổi dự lễ trao thưởng, các học sinh được xếp thành 1 hàng ngang. Xác suất để xếp cho 2 học sinh nữ không đứng cạnh nhau là:
A. ;
B. ;
C. ;
D. .
Câu 29. Một dãy phố có 5 cửa hàng bán quần áo. Có 5 người khách đến mua quần áo, mỗi người khách vào ngẫu nhiên một trong năm cửa hàng đó. Xác suất để có một cửa hàng có 3 người khách là:
A.
B.
C.
D.
Câu 30. Chọn ngẫu nhiên 2 học sinh từ một tổ có 9 học sinh. Biết rằng xác suất chọn được 2 học sinh nữ bằng , hỏi tổ có bao nhiêu học sinh nữ?
A. 6;
B. 5;
C. 3;
D. 4.
Câu 1:
Chọn khẳng định sai trong các khẳng định sau:
A. Phép thử ngẫu nhiên (gọi tắt là phép thử) là một hoạt động mà ta không thể biết trước được kết quả của nó;
B. Tập hợp tất cả các kết quả có thể có của phép thử ngẫu nhiên được gọi là không gian mẫu;
C. Với mọi biến cố A, 0 ≤ P(A) ≤ 1;
D. Xác suất của mỗi biến cố đo lường xảy ra của biến cố đó. Biến cố có khả năng xảy ra càng cao thì xác suất của nó càng xa 1.
Câu 2:
Xúc xắc có 6 mặt đánh số chấm từ 1 đến 6 chấm. Không gian mẫu của 1 lần tung xúc xắc là:
A. = {1; 2; 3; 4; 5; 6};
B. = 1; 2; 3; 4; 5; 6;
C. = {1}; {2}; {3}; {4}; {5}; {6};
D. = ∅.
Câu 3:
Tung xúc xắc 5 lần sẽ có không gian mẫu gồm bao nhiêu cách xuất hiện mặt của xúc xắc?
A. 6!;
B. 30;
C. 65
D. vô số.
Câu 4:
Chọn khẳng định đúng trong các khẳng định sau:
A. Phép thử ngẫu nhiên (gọi tắt là phép thử) là một hoạt động mà ta không thể biết trước được kết quả của nó;
B. Cho A là một biến cố. Khi đó biến cố “Không xảy ra A”, kí hiệu là , được gọi là biến cố đối của A;
C. P( ) = 1, P(∅) = 0;
D. Cả A, B, C đều đúng.
Câu 5:
Một ban đại diện gồm 5 người được thành lập từ 10 người có tên sau đây: Lan, Mai, Minh, Thu, Miên, An, Hà, Thanh, Mơ, Nga. Tính xác xuất để ít nhất 3 người trong ban đại diện có tên bắt đầu bằng chữ M.
A. 5/252
B. 1/24
C. 5/21
D. 11/42
Câu 6:
Một hộp chứa 18 quả cầu gồm 8 quả cầu màu xanh và 10 quả cầu màu trắng. Chọn ngẫu nhiên 2 quả từ hộp đó. Xác xuất để chọn được 2 quả cầu cùng màu là:
A. 12/17
B. 5/17
C. 73/153
D. 80/153
Câu 7:
Điền tiếp vào chỗ trống: “Giả sử một phép thử có không gian mẫu gồm …. các kết quả có cùng khả năng xảy ra và A là một biến cố. Xác suất của biến cố A là một số, kí hiệu là P(A), được xác định bởi công thức:
P(A) =
trong đó n(A) và n( ) lần lượt là kí hiệu số phần tử của tập A và ”.
A. vô hạn;
B. hữu hạn;
C. tất cả;
D. vô số.
Câu 8:
Trên bàn có 5 quả táo và 5 quả cam. Xác định số phần tử không gian mẫu của phép thử lấy 3 quả ở trên bàn sau đó bỏ ra ngoài lấy tiếp 2 quả nữa.
A. 2 520 phần tử;
B. 5 220 phần tử;
C. 1 050 phần tử;
D. 2 150 phần tử.
Câu 9:
Cho tập hợp A gồm các số nguyên dương nhỏ hơn hoặc bằng 40. Chọn 2 phần tử trong tập hợp A. Gọi B là biến cố “Phần tử được chọn chia hết cho 5”. Số kết quả thuận lợi cho biến cố B là:
A. 26;
B. 27;
C. 25;
D. 28.
Câu 10:
Từ các chữ số {1; 2; 3; 4; 5; 6}, lập một số bất kì gồm 3 chữ số. Xác suất để số nhận được chia hết cho 6 là:
A. 1/2
B. 1/4
C. 1/6
D. 1/8
Câu 11:
Hai người ngang tài ngang sức tranh chức vô địch của một cuộc thi cờ vua. Người dành chiến thắng là người đầu tiên thắng được 5 ván cờ. Tại thời điểm người chơi thứ nhất đã thắng 4 ván và người chơi thứ hai mới thắng 2 ván (không có ván nào hòa). Xác suất để người chơi thứ nhất dành chiến thắng là:
A. 7/8
B. 4/5
C. 3/4
D. 1/2
Câu 12:
Một người bỏ ngẫu nhiên 4 lá thư vào 4 bì thư đã được ghi sẵn địa chỉ cần gửi. Xác xuất để có ít nhất 1 lá thư bỏ đúng phong bì của nó là:
A. 5/8
B. 4/7
C. 3/8
D. Không xác định.
Câu 13:
Một tổ có 7 học sinh nam và 3 học sinh nữ. Cô giáo chọn ngẫu nhiên 2 bạn trong tổ lên kiểm tra bài cũ. Xác suất để 2 bạn chọn lên là 2 bạn nữ là:
A. 1/15
B. 7/15
C. 8/15
D. 14/55
Câu 14:
Trong các thí nghiệm sau thí nghiệm nào không phải là phép thử ngẫu nhiên:
A. Gieo đồng tiền xem xuất hiện mặt ngửa hay mặt sấp;
B. Gieo 3 đồng tiền và xem có mấy đồng tiền lật ngửa;
C. Chọn bất kì 1 học sinh trong lớp và xem là nam hay nữ;
D. Bỏ hai viên bi xanh và ba viên bi đỏ trong một chiếc hộp, sau đó lấy từng viên một để đếm xem có tất cả bao nhiêu viên bi.
Câu 15:
Gieo hai đồng tiền một lần. Kí hiệu S, N lầm lượt để chỉ đồng tiền lật sấp, lật ngửa. Xác định biến cố M: “Hai đồng tiền xuất hiện hai mặt không giống nhau”.
A. M = {NN, SS};
B. M = {NS, SN};
C. M = {NS, NN};
D. M = {SS, SN}.
Câu 16:
Một hộp có:
• 2 viên bi trắng được đánh số từ 1 đến 2;
• 3 viên bi xanh được đánh số từ 3 đến 5;
• 2 viên bi đỏ được đánh số từ 6 đến 7.
Lấy ngẫu nhiên hai viên bi, mô tả không gian mẫu nào dưới đây là đúng?
A. Ω = {(m, n)| 1 ≤ m ≤ 7, 1 ≤ n ≤ 7};
B. Ω = {(m, n)| 1 ≤ m ≤ 5, 6 ≤ n ≤ 7};
C. Ω = {(m, n)| 1 ≤ m ≤ 7, 1 ≤ n ≤ 7, m ≠ n};
D. Ω = {(m, n)| 1 ≤ m ≤ 3, 4 ≤ n ≤ 7}.
Câu 17:
Cho tập hợp A gồm các số nguyên dương nhỏ hơn hoặc bằng 60. Chọn 1 phần tử trong tập hợp A. Gọi B là biến cố “Phần tử được chọn chia hết cho 10”. Số kết quả thuận lợi cho biến cố B là:
A. 6;
B. 7;
C. 5;
D. 9.
Câu 18:
Trên bàn có 3 quả táo và 4 quả cam. Xác định số phần tử không gian mẫu của phép thử lấy 2 quả ở trên bàn sau đó bỏ ra ngoài rồi lấy tiếp 1 quả nữa.
A. 7 phần tử;
B. 5 phần tử;
C. 105 phần tử;
D. 21 phần tử.
Câu 19:
Trong một chiếc hộp đựng 6 viên bi đỏ, 8 viên bi xanh, 10 viên bi trắng. Lấy ngẫu nhiên 4 viên bi. Số kết quả thuận lợi cho biến cố B: “4 viên bi lấy ra có ít nhất một viên bi màu xanh” là:
A. 10 626;
B. 1 820;
C. 7 566;
D. 8 806.
Câu 20:
Gieo một con xúc xắc. Xác suất để mặt chấm chẵn xuất hiện là?
A. 0,2;
B. 0,3;
C. 0,4;
D. 0,5.
Câu 21:
Trong hộp có 3 viên bi xanh và 5 viên bi đỏ. Lấy ngẫu nhiên trong hộp 3 viên bi. Xác suất của biến cố A: “Lấy ra được 3 viên bi màu đỏ” là:
A. P(A) = 13/28
B. P(A) = 5/28
C. P(A) = 23/28
D. P(A) = 3/28
Câu 22:
Tung một đồng xu cân đối và đồng chất 3 lần liên tiếp. Xác suất của biến cố A: “Trong 3 lần tung có ít nhất 1 lần xuất hiện mặt sấp” là:
A. P(A) =7/8
B. P(A) =1/2
C. P(A) =3/8
D. P(A) =1/8
Câu 23:
Trong hộp có 6 quả cầu đỏ và 4 quả cầu xanh, lấy ngẫu nhiên đồng thời 4 quả cầu. Xác suất để 4 quả cầu lấy ra cùng màu là:
A. P = 8/105
B. P =18/105
C. P = 24/105
D. P = 4/53
Câu 24:
Một cái túi chứa 3 viên bi đỏ và 5 bi xanh, 6 viên bi vàng. Chọn ngẫu nhiên 3 viên bi. Xác suất để 3 viên bi có cả ba màu đỏ, xanh, vàng là:
A. 45/182
B. 12/34
C. 1
D. 56/182
Câu 25:
Lớp 11B có 20 học sinh gồm 12 nữ và 8 nam. Cần chọn ra 2 học sinh của lớp đi lao động. Xác suất để chọn được 2 học sinh trong đó có cả nam và nữ là:
A. 14/95
B. 48/95
C. 33/95
D. 47/95
Câu 26:
Gieo một con xúc xắc cân đối và đồng chất. Giả sử xúc xắc xuất hiện mặt b chấm. Xác suất để phương trình x2 + bx + 2 = 0 có hai nghiệm phân biệt là:
A. 3/5
B. 5/6
C. 1/3
D. 2/3
Câu 27:
Một hộp đựng 9 viên bi có kích thước và khối lượng như nhau, trong đó có 4 viên bi đỏ và 5 viên bi xanh. Lấy ngẫu nhiên từ hộp 3 viên bi. Xác suất để 3 viên bi lấy ra có ít nhất 2 viên bi màu xanh là:
A. 5/42
B. 10/21
C. 5/14
D. 25/42
Câu 28:
Đội tuyển của một lớp có 8 học sinh nam và 4 học sinh nữ. Trong buổi dự lễ trao thưởng, các học sinh được xếp thành 1 hàng ngang. Xác suất để xếp cho 2 học sinh nữ không đứng cạnh nhau là:
A. 653/660
B. 7/660
C. 21/55
D. 14/55
Câu 29:
Một dãy phố có 5 cửa hàng bán quần áo. Có 5 người khách đến mua quần áo, mỗi người khách vào ngẫu nhiên một trong năm cửa hàng đó. Xác suất để có một cửa hàng có 3 người khách là:
A. 3/125
B. 181/625
C. 24/125
D. 32/125
Câu 30:
Chọn ngẫu nhiên 2 học sinh từ một tổ có 9 học sinh. Biết rằng xác suất chọn được 2 học sinh nữ bằng 5/18 , hỏi tổ có bao nhiêu học sinh nữ?
A. 6;
B. 5;
C. 3;
D. 4.
Câu 1:
A. Biến cố không thể;
B. Biến cố chắc chắn;
C. Phép thử;
Câu 2:
Cho biến cố A có không gian mẫu Ω và là biến cố đối của biến cố A. Khẳng định nào sau đây sai?
A. n(Ω) = P(A).n(A);
B. ;
C. ;
Câu 3:
Nguyên lí xác suất bé được phát biểu như thế nào?
A. Nếu một biến cố có xác suất rất bé thì trong một phép thử, biến cố đó có xác suất bằng 0;
B. Nếu một biến cố có xác suất rất bé thì trong một phép thử, biến cố đó không chắc sẽ xảy ra;
C. Nếu một biến cố có xác suất rất bé thì trong một phép thử, biến cố đó chắc chắn sẽ xảy ra;
Câu 4:
Mệnh đề nào sau đây đúng?
A. Biến cố chắc chắn là biến cố không bao giờ xảy ra;
B. Mỗi tập con của không gian mẫu được gọi là một biến cố;
C. Một kết quả thuộc biến cố A được gọi là kết quả làm cho biến cố A không xảy ra;
Câu 5:
Một hộp chứa 4 quả cầu trắng và 6 quả cầu xanh có kích thước và khối lượng như nhau. Lấy ngẫu nhiên 3 quả cầu từ trong hộp. Hoạt động nào sau đây không phải là biến cố của phép thử trên?
A. Ba quả cầu lấy ra cùng màu với nhau;
B. Ba quả cầu lấy ra có ít nhất một quả màu trắng;
C. Ba quả cầu lấy ra gồm có ba màu;
Câu 6:
Cho biến cố A có không gian mẫu là Ω và là biến cố đối của biến cố A. Khẳng định nào sau đây sai?
A. P(A) ≥ 0, với mọi biến cố A;
B. P(∅) = 0;
C. P(Ω) > 1;
Câu 7:
Lấy ngẫu nhiên hai viên bi từ một thùng có 4 bi xanh, 5 bi đỏ và 6 bi vàng. Số phần tử của không gian mẫu là:
A. 30;
B. 17;
C. 105;
Câu 8:
Một cầu thủ sút bóng vào cầu môn một lần. Biết rằng xác suất sút vào cầu môn là . Xác suất không sút vào cầu môn của cầu thủ đó bằng:
A.
B.
C.
D. 0
Câu 9:
Hai xạ thủ bắn vào một tấm bia, xác suất bắn trúng bia của xạ thủ 1 và 2 lần lượt là 0,8 và 0,7. Xạ thủ nào có khả năng bắn trúng thấp hơn?
A. Xạ thủ 1;
B. Xạ thủ 2;
C. Cả hai xạ thủ đều có khả năng bắn trúng như nhau;
Câu 10:
Cho phép thử có không gian mẫu là Ω = {1; 2; 3; 4; 5; 6}. Các cặp biến cố không đối nhau là:
A. A = {1} và B = {2; 3; 4; 5; 6};
B. C = {1; 4; 5} và D = {2; 3; 6};
C. E = {1; 4; 6} và F = {2; 3};
Câu 1:
Từ một hộp chứa 11 quả cầu đỏ và 4 quả cầu xanh, lấy ngẫu nhiên đồng thời 3 quả cầu. Xác suất để lấy được 3 quả cầu màu xanh là:
A.
B.
C.
D.
Câu 2:
Tung một đồng tiền và gieo một con xúc xắc một lần. Số phần tử của không gian mẫu là:
A. 24;
B. 12;
C. 6;
Câu 3:
Gieo ngẫu nhiên một xúc xắc 6 mặt cân đối và đồng chất. Xác suất của biến cố A: “Mặt xuất hiện có số chấm chia hết cho 3” là:
A. 1
B.
C.
D.
Câu 4:
Một bể cá gồm 5 con cá Koi và 7 con cá vàng. Một người vớt ngẫu nhiên 4 con cá từ bể cá đó. Số kết quả thuận lợi của biến cố X: “Vớt được 2 con cá Koi và 2 con cá vàng” là:
A. 210;
B. 201;
C. 31;
Câu 5:
Gieo một đồng xu cân đối và đồng chất ba lần. Xét biến cố A: “Mặt ngửa xuất hiện ít nhất 1 lần”. Tập hợp nào sau đây mô tả biến cố A?
A. A = {SSN, NSS, SNN, NNS, NNN};
B. A = {SSN, SNS, NSS, NNN};
C. A = {SSN, SNS, NSS, SNN, NSN, NNS, NNN};
Câu 6:
Trong hộp có 2 000 nắp khoen bia Tiger, trong đó có 2 nắp ghi “Chúc mừng bạn đã trúng thưởng xe Ford”. Bạn được chọn lên rút thăm lần lượt hai nắp khoen. Xác suất để cả hai nắp khoen đều trúng thưởng là:
A.
B.
C.
D.
Câu 7:
Trong giỏ có 5 đôi tất khác màu, các chiếc tất cùng đôi thì cùng màu. Lấy ngẫu nhiên 2 chiếc tất. Xác suất để 2 chiếc đó cùng màu là:
A.
B.
C.
D.
Câu 8:
Trên giá sách có 4 quyển sách Toán, 3 quyển sách Vật lí và 2 quyển sách Hóa học. Lấy ngẫu nhiên 3 quyển sách. Xác suất để trong 3 quyển sách được lấy ra có ít nhất một quyển sách Toán là:
A.
B.
C.
D.
Câu 9:
Chọn ngẫu nhiên một số tự nhiên có 4 chữ số khác nhau. Gọi A là biến cố “Số tự nhiên được chọn gồm 4 số 3; 4; 5; 6”. Xác suất của biến cố A là:
A.
B.
C.
D.
Câu 10:
Một tổ có 9 học sinh, trong đó có 5 học sinh nam và 4 học sinh nữ được xếp thành hàng dọc. Xác suất sao cho 5 học sinh nam đứng kề nhau là:
A.
B.
C.
D.
Câu 1:
Có năm đoạn thẳng có độ dài lần lượt là 1 cm, 3 cm, 5 cm, 7 cm và 9 cm. Chọn ngẫu nhiên ba đoạn thẳng trong số năm đoạn thẳng trên. Xác suất để ba đoạn thẳng được chọn lập thành một tam giác là:
A.
B.
C.
D.
Câu 2:
Một hộp quà đựng 16 dây buộc tóc cùng chất liệu, cùng kiểu dáng nhưng khác nhau về màu sắc. Trong hộp có 8 dây xanh, 5 dây đỏ, 3 dây vàng. Bạn Hoa được chọn ngẫu nhiên 6 dây từ hộp quà để làm phần thưởng cho mình. Xác suất để trong 6 dây bạn Hoa chọn có ít nhất 1 dây vàng và có không quá 4 dây đỏ là:
A.
B.
C.
D.
Câu 3:
Một hộp chứa 3 viên bi xanh, 5 viên bi đỏ và 6 viên bi vàng. Lấy ngẫu nhiên 6 viên bi từ hộp. Xác suất để 6 viên bi được lấy ra có đủ cả 3 màu là:
A.
B.
C.
D.
Câu 4:
Trong một buổi liên hoan có 10 cặp nam nữ, trong đó có 4 cặp vợ chồng. Chọn ngẫu nhiên 3 người để biểu diễn một tiết mục văn nghệ. Xác suất để 3 người được chọn không có cặp vợ chồng nào là:
A.
B.
C.
D.
Câu 5:
Trong buổi sinh hoạt nhóm của lớp, tổ một có 12 học sinh gồm 4 học sinh nữ trong đó có Mai và 8 học sinh nam trong đó có Đức. Chia tổ thành 3 nhóm, mỗi nhóm gồm 4 học sinh và phải có ít nhất 1 học sinh nữ. Số kết quả thuận lợi cho biến cố A: “Mai và Đức cùng một nhóm” là:
A. 2 100;
B. 1 470;
C. 840;
Câu 6:
Xếp ngẫu nhiên 10 học sinh gồm 5 học sinh nam (trong đó có Bình) và 5 học sinh nữ (trong đó có Phương) thành một hàng ngang. Số kết quả thuận lợi cho biến cố A: “Trong 10 học sinh trên không có hai học sinh cùng giới đứng cạnh nhau, đồng thời Bình và Phương cũng không đứng cạnh nhau” là:
A. 4 608;
B. 9 216;
C. 13 824;
Câu 7:
Có 4 hành khách bước lên một đoàn tàu gồm 4 toa. Mỗi hành khách độc lập với nhau và chọn ngẫu nhiên một toa. Xác suất để 1 toa có 3 người, 1 toa có 1 người và 2 toa còn lại không có ai là:
A.
B.
C.
D.
Câu 8:
Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có tọa độ các đỉnh A(–2; 0), B(–2; 2), C(4; 2), D(4; 0). Chọn ngẫu nhiên một điểm có tọa độ (x; y) (với x, y là các số nguyên) nằm trong hình chữ nhật ABCD, kể cả các điểm nằm trên cạnh. Gọi A là biến cố “x, y đều chia hết cho 2”. Xác suất của biến cố A là:
A.
B.
C. 1
D.
Câu 9:
Gieo một con xúc xắc cân đối và đồng chất. Giả sử xúc xắc xuất hiện mặt b chấm. Xác suất để phương trình x2 + bx + 2 = 0 có hai nghiệm phân biệt là:
A.
B.
C.
D.
Câu 10:
Gieo một con xúc xắc cân đối và đồng chất. Giả sử con xúc xắc xuất hiện mặt b chấm. Xác suất sao cho phương trình x2 – bx + b – 1 = 0 (x là ẩn số) có nghiệm lớn hơn 3 là:
A.
D.