15 Bài tập Giá trị lượng giác của một góc từ 0 đến 180 Trắc nghiệm Toán 10 (có đáp án) - Chân trời sáng tạo
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Giá trị lượng giác của một góc từ 0 đến 180 Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Chân trời sáng tạo sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
15 Bài tập Giá trị lượng giác của một góc từ 0 đến 180 Trắc nghiệm Toán 10 (có đáp án) - Chân trời sáng tạo
Câu 1. Cho α là góc tù. Khẳng định nào sau đây là đúng ?
A. sin α < 0;
B. cos α > 0;
C. tan α < 0;
D. cot α > 0.
Hiển thị đáp án
Đáp án đúng là: C
Nếu α là góc tù thì sinα > 0, cosα < 0, tanα < 0, cotα < 0.
Vậy ta chọn phương án C.
Câu 2. Cho hai góc α và β (0° ≤ α, β ≤ 180°) với α + β = 90°. Giá trị của biểu thức P = cosα.cosβ ‒ sinα.sinβ là:
A. P = 0;
B. P = 1;
C. P = ‒ 1;
D. P = 2.
Hiển thị đáp án
Đáp án đúng là: A
Hai góc α và β (0° ≤ α, β ≤ 180°) là hai góc phụ nhau (do α + β = 90°) nên sinα = cosβ; cosα = sinβ.
Do đó, P = cosα.cosβ – sinβ.sinα = cosα. sinα – cosα.sinα = 0.
Vậy P = 0.
Câu 3. Trong các đẳng thức sau, đẳng thức nào đúng ?
A. sin(180° – α) = ‒cos α;
B. sin(180° – α) = ‒sin α;
C. sin(180° – α) = sin α;
D. sin(180° – α) = cos α.
Hiển thị đáp án
Đáp án đúng là: C
Với mọi góc α thoả mãn 0° ≤ α ≤ 180°, ta luôn có: sin(180° ‒ α) = sinα.
Vậy ta chọn phương án C.
Câu 4. Cho tam giác ABC. Giá trị biểu thức sinA.cos(B + C) + cosA.sin(B + C) là:
A. ‒1;
B. 0;
C. 1;
D. 2.
Hiển thị đáp án
Đáp án đúng là: B
Xét tam giác ABC ta có: (định lí tổng ba góc trong tam giác)
⇒ B ^ + C ^ = 180 ° − A ^
⇒
Và sin(B + C) = sin(180° ‒ A)= sinA.
Do đó:
sinA.cos(B + C) + cosA.sin(B + C)
= sinA.(‒cosA) + cosA.sinA
= ‒sinA.cosA + cosA.sinA
= 0
Vậy sinA.cos(B + C) + cosA.sin(B + C) = 0.
Câu 5. Giá trị cos135° + sin135° bằng bao nhiêu?
A. 3 ;
B. 0;
C. 1;
D. 2 .
Hiển thị đáp án
Đáp án đúng là: B
Ta có: c o s 135 ° = − 2 2 ; sin 135 ° = 2 2 ;
Do đó: cos135° + sin135° = − 2 2 + 2 2 = 0
Vậy cos135° + sin135° = 0.
Câu 6. Trong các đẳng thức sau, đẳng thức nào sai ?
A. sin0° + cos0° = 0;
B. sin90° + cos90° = 1;
C. sin180° + cos180° = ‒1;
D. s i n 60 ° + c o s 60 ° = 3 + 1 2 .
Hiển thị đáp án
Đáp án đúng là: A
Ta có:
+) sin0° + cos0° = 0 + 1 = 1. Do đó phương án A là mệnh đề sai.
+) sin90° + cos90° = 1 + 0 = 1. Do đó phương án B là mệnh đề đúng.
+) sin180° + cos180° = 0 + (‒1) = ‒1. Do đó phương án C là mệnh đề đúng.
+) s i n 60 ° + c o s 60 ° = 3 2 + 1 2 = 3 + 1 2 .
Vậy ta chọn phương án A.
Câu 7. Giá trị của biểu thức: P = cos0° + cos1° + cos2° + ... + cos178° + cos179° + cos180° thuộc khoảng nào sau đây?
A. (0;1);
B. (‒1;1);
C. (1;2);
D. (‒1;0).
Hiển thị đáp án
Đáp án đúng là: B
Ta có:
cos180° = cos(180° ‒ 0°) = ‒cos0° Þ cos0° + cos180° = 0;
cos179° = cos(180° ‒ 1°) = ‒cos1° Þ cos1° + cos179° = 0;
cos178° = cos(180° ‒ 2°) = ‒cos2° Þ cos2° + cos178° = 0;
…
cos91° = cos(180° ‒ 89°) = ‒cos89° Þ cos89° + cos91° = 0.
Suy ra: P = cos0° + cos1° + cos2° + ... + cos178° + cos179° + cos180°
= (cos0° + cos180°) + (cos1° + cos179°) + ... + (cos89° + cos91°) + cos90°
= 0 + 0 + ... + 0 + 0
= 0.
Do đó P = 0.
Vậy giá trị của biểu thức P = 0 thuộc khoảng (‒1;1).
Câu 8. Giá trị biểu thức A = sin30°.cos60° + sin60°.cos30° là:
A. A = 1;
B. A = 0;
C. A = 3 ;
D. A = - 3 ;
Hiển thị đáp án
Đáp án đúng là: A
Ta có:
A = sin30°.cos60° + sin60°.cos30°
A = 1 2 . 1 2 + 3 2 . 3 2 = 1 4 + 3 4 = 4 4 = 1.
Vậy A = 1.
Câu 9. Cho góc α (0° ≤ α ≤ 180°) với tanα = ‒3. Giá trị của bằng P = 6 sin α − 7 cos α 7 sin α + 6 cos α
A. P = 4 3 ;
B. P = − 4 3 ;
C. P = − 5 3 ;
D. P = 5 3 .
Hiển thị đáp án
Đáp án đúng là: D
Vì tanα = ‒3 nên sin α c o s α = − 3
Ta có: P = 6 sin α − 7 cos α 7 sin α + 6 cos α
P = 6 sin α − 7 cos α c o s α 7 sin α + 6 cos α c o s α
P = 6 sin α cos α − 7 7 sin α cos α + 6
P = 6 tan α − 7 7 tan α + 6
P = 6. − 3 − 7 7 − 3 + 6 = − 25 − 15 = 5 3
Vậy P = 5 3 .
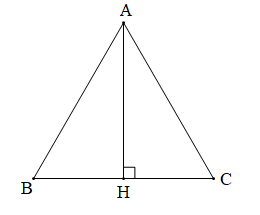
Câu 10. Tam giác đều ABC có đường cao AH. Khẳng định nào sau đây là đúng ?
A. c o s B A H ^ = 1 3 ;
B. sin A B C ^ = 3 2 ;
C. sin A H C ^ = 1 2 ;
D. sin B A H ^ = 3 2 .
Hiển thị đáp án
Đáp án đúng là: B
Tam giác ABC là tam giác đều nên có ba góc bằng 60°.
Do đósin A B C ^ = sin 60 ° = 3 2 .
AH là đường cao của tam giác đều ABC nên B A H ^ = 30 ° , A H C ^ = 90 °
⇒ c o s B A H ^ = c o s 30 ° = 3 2 ; sin B A H ^ = sin 30 ° = 1 2 sin A H C ^ = sin 90 ° = 1.
Do đó phương án A, C và D là sai.
Vậy ta chọn phương án B.
Câu 11. Cho góc α (0° ≤ α ≤ 180°). Trong các khẳng định sau, khẳng định nào sai ?
A. sin2 α + cos2 α = 1;
B. tanα.cotα = 1 (0° < α < 180° và α ≠ 90°);
C. 1 + tan 2 α = 1 c o s 2 α α ≠ 90 ° ;
D. 1 + cot 2 α = 1 c o s 2 α 0 ° < α < 180 ° v à α ≠ 90 ° .
Hiển thị đáp án
Đáp án đúng là: D
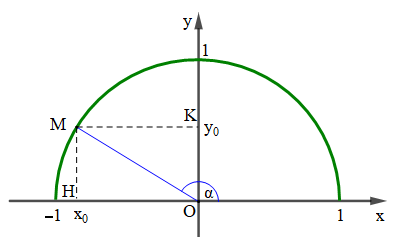
Với mỗi góc α (0° ≤ α ≤ 180°) ta xác định được một điểm M duy nhất trên nửa đường tròn đơn vị sao cho x O M ^ = α 0 ; y0 ) là toạ độ điểm M, ta có:
- Tung độ y0 của M là sin của góc α, kí hiệu là sinα = y0 ;
- Hoành độ x0 của M là côsin của góc α, kí hiệu là cosα = x0 ;
- Tỉ số y 0 x 0 0 ≠ 0) là tang của góc α, kí hiệu là tan α = y 0 x 0 ;
- Tỉ số x 0 y 0 0 ≠ 0) là côtang của góc α, kí hiệu là cot α = x 0 y 0 .
Gọi H và K lần lượt là hình chiếu của M lên Ox và Oy.
Khi đó ta có: OH = x0 = cosα, MH = OK = y0 = sinα, OM = 1.
Tam giác OMH vuông tại H, áp dụng định lí Pythagore ta có:
MH2 + OH2 = OM2
Hay sin2 α + cos2 α = 1.
Do đó phương án A là mệnh đề đúng.
Với 0° < α < 180° và α ≠ 90° ta có: tan α = y 0 x 0 ; cot α = x 0 y 0 .
⇒ tan α . cot α = y 0 x 0 . x 0 y 0 = 1.
Với α ≠ 90° ta có: 1 + tan 2 α = 1 + sin 2 α cos 2 α = cos 2 α + sin 2 α cos 2 α = 1 c o s 2 α 2 α + cos2 α = 1).
Do đó phương án C là mệnh đề đúng.
Với 0° < α < 180° và α ≠ 90° ta có:
1 + cot 2 α = 1 + cot 2 α sin 2 α = sin 2 α + cos 2 α sin 2 α = 1 sin 2 α 2 α + cos2 α = 1).
Do đó phương án D là mệnh đề sai.
Vậy ta chọn phương án D.
Câu 12. Cho hai góc α và β (0° ≤ α, β ≤ 180°) với α + β = 180°, giá trị của biểu thức: M = cosα.cosβ – sinβ.sinα là:
A. M = ‒1;
B. M = 2;
C. M = 0;
D. M = 1.
Hiển thị đáp án
Đáp án đúng là: A
Vì hai góc α và β (0° ≤ α, β ≤ 180°) là hai góc bù nhau (do α + β = 180°) nên:
cosβ = ‒cosα và sinβ = sinα.
Ta có: M = cosα.cosβ – sinβ.sinα
M = cosα.(‒cosα) ‒ sinα.sinα = ‒cos2 α ‒ sin2 α
M = ‒(cos2 α + sin2 α)
Mà cos2 α + sin2 α = 1 (đã chứng minh ở Câu 11 ).
Vậy M = ‒1.
Câu 13. Cho góc α với c o s α = − 3 2 2 α – 3tanα + cot3 α là:
A. 1 4 − 4 3 .
B. 1 2 − 2 3 ;
C. 1 4 − 2 3 ;
D. 1 2 − 4 3 .
Hiển thị đáp án
Đáp án đúng là: C
Ta có: c o s α = − 3 2 ⇒
Suy ra: s i n α = 1 2 ; tan α = − 3 3 ; cot α = − 3
Khi đó: A = sin2 α – 3tanα + cot3 α = 1 2 2 − 3. − 3 3 + − 3 3
A = 1 4 + 3 − 3 3 = 1 4 − 2 3 .
Vậy A = 1 4 − 2 3 .
Câu 14. Giá trị của cot22°12'21'' gần với giá trị nào nhất trong các giá trị nào dưới đây?
A. 0,41;
B. 2,45;
C. 0,4;
D. 2,44.
Hiển thị đáp án
Đáp án đúng là: B
Để tính cot22°12'21'' ta sử dụng máy tính cầm tay tính tan22°12'21'' và sau đó tính 1 tan 22 ° 12 ' 21 ' '
Sau khi sử dụng máy tính cầm tay ta tính được cot22°12'21'' = 2,449712232…
Vậy cot22°12'21'' ≈ 2,45.
Câu 15. Giá trị α (0° ≤ α ≤ 180°) thoả mãn tanα = 1,607 gần nhất với giá trị:
A. 0.03°;
B. 3°;
C. 58°;
D. 122°;
Hiển thị đáp án
Đáp án đúng là: C
Để tìm α khi biết tanα = 1,607 thì ta sử dụng máy tính cầm tay và tính được: α ≈ 58°.
Vậy α ≈ 58°.
Câu 1:
Cho α là góc tù. Khẳng định nào sau đây là đúng ?
A. sin α < 0;
B. cos α > 0;
C. tan α < 0;
D. cot α > 0.
Xem lời giải »
Câu 2:
Cho hai góc α và β (0° ≤ α, β ≤ 180°) với α + β = 90°. Giá trị của biểu thức P = cosα.cosβ ‒ sinα.sinβ là:
A. P = 0;
B. P = 1;
C. P = ‒ 1;
D. P = 2.
Xem lời giải »
Câu 3:
Trong các đẳng thức sau, đẳng thức nào đúng ?
A. sin(180° – α) = ‒cos α;
B. sin(180° – α) = ‒sin α;
C. sin(180° – α) = sin α;
D. sin(180° – α) = cos α.
Xem lời giải »
Câu 4:
Cho tam giác ABC. Giá trị biểu thức sinA.cos(B + C) + cosA.sin(B + C) là:
A. ‒1
B. 0
C. 1
D. 2
Xem lời giải »
Câu 5:
Giá trị cos135° + sin135° bằng bao nhiêu?
A. 3 ;
B. 0
C. 1
D. 2
Xem lời giải »
Câu 6:
Trong các đẳng thức sau, đẳng thức nào sai ?
A. sin0° + cos0° = 0;
B. sin90° + cos90° = 1;
C. sin180° + cos180° = ‒1;
D. s i n 60 ° + c o s 60 ° = 3 + 1 2 .
Xem lời giải »
Câu 7:
Giá trị của biểu thức: P = cos0° + cos1° + cos2° + ... + cos178° + cos179° + cos180° thuộc khoảng nào sau đây?
A. (0;1);
B. (‒1;1);
C. (1;2);
D. (‒1;0).
Xem lời giải »
Câu 8:
Giá trị biểu thức A = sin30°.cos60° + sin60°.cos30° là:
A. A = 1;
B. A = 0;
C. A = 3 ;
D. A = - 3
Xem lời giải »
Câu 9:
Cho góc α (0° ≤ α ≤ 180°) với tanα = ‒3. Giá trị của P = 6 sin α − 7 cos α 7 sin α + 6 cos α bằng bao nhiêu?
A. P = 4 3 ;
B. P = - 4 3 ;
C. P = − 5 3 ;
D. P = 5 3 .
Xem lời giải »
Câu 10:
Tam giác đều ABC có đường cao AH. Khẳng định nào sau đây là đúng ?
A. c o s B A H ^ = 1 3 ;
B. sin A B C ^ = 3 2 ;
C. sin A H C ^ = 1 2 ;
D. sin B A H ^ = 3 2 .
Xem lời giải »
Câu 11:
Cho góc α (0° ≤ α ≤ 180°). Trong các khẳng định sau, khẳng định nào sai ?
A. sin2 α + cos2 α = 1;
B. tanα.cotα = 1 (0° < α < 180° và α ≠ 90°);
C. 1 + tan 2 α = 1 c o s 2 α α ≠ 90 ° ;
D. 1 + cot 2 α = 1 c o s 2 α 0 ° < α < 180 ° v à α ≠ 90 ° .
Xem lời giải »
Câu 12:
Cho hai góc α và β (0° ≤ α, β ≤ 180°) với α + β = 180°, giá trị của biểu thức: M = cosα.cosβ – sinβ.sinα là:
A. M = ‒1;
B. M = 2;
C. M = 0;
D. M = 1.
Xem lời giải »
Câu 13:
Cho góc α với c o s α = − 3 2 . Giá trị của biểu thức: A = sin2 α – 3tanα + cot3 α là:
A. 1 4 − 4 3 .
B. 1 2 − 2 3 ;
C. 1 4 − 2 3 ;
D. 1 2 − 4 3 .
Xem lời giải »
Câu 14:
Giá trị của cot22°12'21'' gần với giá trị nào nhất trong các giá trị nào dưới đây?
A. 0,41;
B. 2,45;
C. 0,4;
D. 2,44.
Xem lời giải »
Câu 15:
Giá trị α (0° ≤ α ≤ 180°) thoả mãn tanα = 1,607 gần nhất với giá trị:
A. 0.03°;
B. 3°;
C. 58°;
D. 122°;
Xem lời giải »
Câu 1:
Kí hiệu \[\tan \alpha = \frac{{{y_0}}}{{{x_0}}}\] (với x0 ≠ 0, 0° ≤ α ≤ 180°) nghĩa là:
A. Tỉ số \[\frac{{{y_0}}}{{{x_0}}}\] (x0 ≠ 0) là sin của góc α ;
B. Tỉ số \[\frac{{{y_0}}}{{{x_0}}}\] (x0 ≠ 0) là cos của góc α ;
C. Tỉ số \[\frac{{{y_0}}}{{{x_0}}}\] (x0 ≠ 0) là tan của góc α ;
D. Tỉ số \[\frac{{{y_0}}}{{{x_0}}}\] (x0 ≠ 0) là cot của góc α.
Xem lời giải »
Câu 2:
Với điểm \[M\left( {\frac{4}{5};\frac{3}{5}} \right)\] , ta gọi \(\widehat {xOM} = \alpha \) . Khẳng định nào sau đây đúng ?
A. \[\sin \alpha = \frac{3}{5}\] và \(co{\rm{s}}\alpha \,{\rm{ = }}\frac{4}{5};\)
B. \[\sin \alpha = \frac{4}{5}\] và \[co{\rm{s}}\alpha \,{\rm{ = }}\frac{3}{5};\]
C. \[\sin \alpha = \frac{{16}}{{25}}\] và \(co{\rm{s}}\alpha \,{\rm{ = }}\frac{9}{{25}}\) ;
D. \[\sin \alpha = \frac{9}{{25}}\] và \[co{\rm{s}}\alpha \,{\rm{ = }}\frac{{16}}{{25}}.\] .
Xem lời giải »
Câu 3:
Với mọi góc α thỏa mãn 0° ≤ α ≤ 180°, ta luôn có sin(90° – α ) và tan(90° – α ) lần lượt bằng:
A. cot α và cos α ;
B. sin α và tan α ;
C. cos α và cot α ;
D. cos α và tan α .
Xem lời giải »
Câu 4:
Với mọi góc α thỏa mãn 0° ≤ α ≤ 180°, ta luôn có cos(180° – α ) bằng:
A. –cosα;
B. cosα;
C. sinα;
D. tanα.
Xem lời giải »
Câu 5:
Giá trị của tan103° bằng:
A. tan77°;
B. –tan77°;
C. cot77°;
D. –cot77°.
Xem lời giải »
Câu 6:
Giá trị của sin30° bằng:
A. \(\frac{{\sqrt 3 }}{2}\) ;
B. \(\frac{1}{2}\) ;
C. \(\frac{{\sqrt 2 }}{2}\) ;
D. \( - \frac{1}{2}\) .
Xem lời giải »
Câu 7:
Nếu góc α thỏa mãn 90° ≤ α ≤ 180° thì:
A. cot α > 0;
B. tan α > 0;
C. cos α > 0;
D. sin α > 0.
Xem lời giải »
Câu 1:
Cho góc x (0° ≤ x ≤ 180°) mà tanx không xác định. Giá trị của x bằng:
A. 30°;
B. 60°;
C. 90°;
D. 120°.
Xem lời giải »
Câu 2:
Sử dụng máy tính cầm tay, giá trị của cot26°32’54’’ xấp xỉ bằng:
A. 2,001;
B. 0,4996;
C. –2,001;
D. 0,4469.
Xem lời giải »
Câu 3:
Giá trị của sin80° bằng:
A. cos10°;
B. sin10°;
C. sin100°;
D. Cả A và C đều đúng.
Xem lời giải »
Câu 4:
Giá trị của biểu thức A = a2 sin90° + b2 cos90° + c2 cos180° bằng:
A. a2 + c2 ;
B. a2 – b2 + c2 ;
C. b2 + c2 ;
D. a2 – c2 .
Xem lời giải »
Câu 5:
Giá trị của biểu thức B = 3 – sin2 90° + 2cos2 60° – 3tan2 45° bằng:
A. 2;
B. \(\frac{1}{2}\) ;
C. \( - \frac{1}{2}\) ;
D. 0.
Xem lời giải »
Câu 6:
Cho hai góc α và β (với 0° ≤ α , β ≤ 180°) thỏa mãn α + β = 180°. Giá trị của biểu thức P = sin α .cos α + sin β .cos β bằng:
A. 0;
B. 1;
C. –1;
D. 2.
Xem lời giải »
Câu 7:
Giá trị của biểu thức M = sin 50° + cos 70° + cos 110° – sin130° bằng:
A. –1;
B. \(\frac{1}{2}\) ;
C. 0;
D. 1;
Xem lời giải »
Câu 8:
Giá trị của biểu thức H = cot5°.cot10°.cot15°…cot80°.cot85° bằng:
A. –1;
B. 1;
C. 0;
D. 2.
Xem lời giải »
Câu 1:
Cho ∆ABC. Khẳng định nào sau đây đúng nhất ?
A. \(\sin \frac{{A + B}}{2} = \cos \frac{C}{2}\) ;
B. \(\tan \frac{{A + B - C}}{2} = \cot C\) ;
C. cos(A + B) = –cosC;
D. Cả A, B, C đều đúng.
Xem lời giải »
Câu 2:
Giá trị của biểu thức M = sin2 45° – 2sin2 50° + 3cos2 45° – 2sin2 130° + 4tan55°.tan35° bằng:
A. 1;
B. 2;
C. 4;
D. 5.
Xem lời giải »
Câu 3:
Cho biết tan α = –3 (0° ≤ α ≤ 180°). Giá trị của \(H = \frac{{6\sin \alpha - 7\cos \alpha }}{{6\cos \alpha + 7\sin \alpha }}\) bằng:
A. \(\frac{4}{3}\) ;
B. \( - \frac{5}{3}\) ;
C. \( - \frac{4}{3}\) ;
D. \(\frac{5}{3}\) .
Xem lời giải »
Câu 4:
Cho biết sin α – cos α = \(\frac{1}{{\sqrt 5 }}\) (0° ≤ α , β ≤ 180°). Giá trị của \(E = \sqrt {{{\sin }^4}\alpha + {{\cos }^4}\alpha } \) bằng:
A. \(\frac{{\sqrt {15} }}{5}\) ;
B. \(\frac{{\sqrt {17} }}{5}\) ;
C. \(\frac{{\sqrt {19} }}{5}\) ;
D. \(\frac{{\sqrt {21} }}{5}\) .
Xem lời giải »
Câu 5:
Cho biết \(2\cos \alpha + \sqrt 2 \sin \alpha = 2\) , với 0° < α < 90°. Giá trị của cotα bằng:
A. \(\frac{{\sqrt 5 }}{4}\) ;
B. \(\frac{{\sqrt 3 }}{4}\) ;
C. \(\frac{{\sqrt 2 }}{2}\) ;
D. \(\frac{{\sqrt 2 }}{4}\) .
Xem lời giải »