15 Bài tập Toạ độ của vectơ Trắc nghiệm Toán 10 (có đáp án) - Chân trời sáng tạo
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Toạ độ của vectơ Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Chân trời sáng tạo sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
15 Bài tập Toạ độ của vectơ Trắc nghiệm Toán 10 (có đáp án) - Chân trời sáng tạo
Câu 1. Trong mặt phẳng Oxy, cho hai điểm A(1; 2) và B(–2; 3). Gọi B’ là điểm đối xứng của B qua A. Tọa độ điểm B’ là:
A. B’(4; 1);
B. B’(0; 1);
C. B’(–4; –1);
D. B’(0; –1).
Câu 2. Cho mặt phẳng Oxy, cho ∆ABC có G là trọng tâm. Biết B(4; 1), C(1; –2) và G(2; 1). Tọa độ điểm A là:
A. A(1; 4);
B. A(3; 0);
C. A(4; 1);
D. A(0; 3).
Câu 3. Trong mặt phẳng Oxy, cho ba điểm A(–2; –3), B(1; 4) và C(3; 1). Đặt . Tọa độ của là:
A. (–2; 3);
B. (–8; –11);
C. (2; –3);
D. (8; 11).
Câu 4. Trong mặt phẳng Oxy, cho ba điểm A(1; 5), B(–1; 0) và C(1; 3). M là điểm nằm trên trục Oy sao cho cùng phương với . Tọa độ điểm M là:
A.
B.
C.
D.
Câu 5. Trong mặt phẳng Oxy, cho và . Tính .
A. 6;
B. 2;
C. 4;
D. –4.
Câu 6. Cho và . Tìm a để .
A. ;
B. ;
C. ;
D. .
Câu 7. Trong mặt phẳng Oxy, cho và . Kết luận nào sau đây sai?
A. ;
B. ;
C. ;
D. .
Câu 8. Trong mặt phẳng Oxy, cho , . Tìm x để và cùng phương.
A. x = –5;
B. x = 4;
C. x = 0;
D. x = –1.
Câu 9. Trong mặt phẳng Oxy, cho , . Tìm tọa độ của sao cho .
A. ;
B. ;
C. ;
D. .
Câu 10. Trong mặt phẳng Oxy, cho ba điểm A(–1; 1), B(1; 3), C(5; 2). Tọa độ điểm D là đỉnh thứ tư của hình bình hành ABCD là:
A. (3; –2);
B. (5; 0);
C. (3; 0);
D. (5; –2).
Câu 11. Trong mặt phẳng Oxy, cho hai điểm A(1; 2) và B(–1; 5). Tìm m để điểm C(2; m) thuộc đường thẳng AB.
A. m = 1;
B. ;
C. ;
D. m = 2.
Câu 12.Cho hai điểm A(6; –1) và B(x; 9). Giá trị của x để khoảng cách giữa A và B bằng là:
A. x ∈∅;
B. x = 1;
C. x = 11;
D. x = 11 hoặc x = 1.
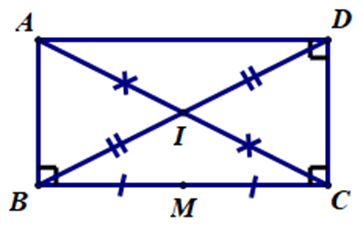
Câu 13. Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có A(0; 3), D(2; 1) và I(–1; 0) là tâm của hình chữ nhật. Tọa độ trung điểm của đoạn thẳng BC là:
A. (–3; –2);
B. (–2; 1);
C. (4; –1);
D. (1; 2).
Câu 14. Cho , . Góc giữa hai vectơ và bằng
A. 45°;
B. 60°;
C. 90°;
D. 135°.
Câu 15. Trong mặt phẳng Oxy, cho ∆ABC có A(–3; 0), B(3; 0) và C(2; 6). Gọi H(a; b) là trực tâm của ∆ABC. Giá trị của a + 6b bằng:
A. 3;
B. 6;
C. 7;
D. 5.
Câu 1:
Trong mặt phẳng Oxy, cho hai điểm A(1; 2) và B(–2; 3). Gọi B’ là điểm đối xứng của B qua A. Tọa độ điểm B’ là:
A. B’(4; 1);
B. B’(0; 1);
C. B’(–4; –1);
D. B’(0; –1).
Câu 2:
Cho mặt phẳng Oxy, cho ∆ABC có G là trọng tâm. Biết B(4; 1), C(1; –2) và G(2; 1). Tọa độ điểm A là:
A. A(1; 4);
B. A(3; 0);
C. A(4; 1);
D. A(0; 3).
Câu 3:
Trong mặt phẳng Oxy, cho ba điểm A(–2; –3), B(1; 4) và C(3; 1). Đặt . Tọa độ của là:
A. (–2; 3);
B. (–8; –11);
C. (2; –3);
D. (8; 11).
Câu 4:
Trong mặt phẳng Oxy, cho ba điểm A(1; 5), B(–1; 0) và C(1; 3). M là điểm nằm trên trục Oy sao cho cùng phương với . Tọa độ điểm M là:
A.
B.
C.
D.
Câu 8:
Trong mặt phẳng Oxy, cho . Tìm x để và cùng phương.
A. x = –5;
B. x = 4;
C. x = 0;
D. x = –1.
Câu 10:
Trong mặt phẳng Oxy, cho ba điểm A(–1; 1), B(1; 3), C(5; 2). Tọa độ điểm D là đỉnh thứ tư của hình bình hành ABCD là:
A. (3; –2);
B. (5; 0);
C. (3; 0);
D. (5; –2).
Câu 11:
Trong mặt phẳng Oxy, cho hai điểm A(1; 2) và B(–1; 5). Tìm m để điểm C(2; m) thuộc đường thẳng AB.
A. m = 1;
B. m = 1/2
C. m = -1/2
D. m = 2
Câu 12:
Cho hai điểm A(6; –1) và B(x; 9). Giá trị của x để khoảng cách giữa A và B bằng là:
B. x = 1;
C. x = 11;
D. x = 11 hoặc x = 1.
Câu 13:
Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có A(0; 3), D(2; 1) và I(–1; 0) là tâm của hình chữ nhật. Tọa độ trung điểm của đoạn thẳng BC là:
A. (–3; –2);
B. (–2; 1);
C. (4; –1);
D. (1; 2).
Câu 15:
Trong mặt phẳng Oxy, cho ∆ABC có A(–3; 0), B(3; 0) và C(2; 6). Gọi H(a; b) là trực tâm của ∆ABC. Giá trị của a + 6b bằng:
A. 3;
B. 6;
C. 7;
D. 5.
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho . Đâu là tọa độ của điểm A?
A. (0; 0);
B. (10; 2);
C. (‒ 10; ‒ 2);
Câu 2:
Trong mặt phẳng tọa độ Oxy cho điểm C có tọa độ là C(‒2; ‒5). Biểu diễn vectơ theo các vectơ đơn vị là
A.
B.
C.
D.
Câu 3:
Trong mặt phẳng tọa độ Oxy cho 2 điểm M(2; 1) và N(1; 2). Tọa độ vectơ là
A. = (1; 1);
B. = (‒1; 1);
C. = (1; ‒1);
Câu 4:
Trong mặt phẳng tọa độ Oxy cho 2 điểm A(2; 5) và B(6; 7). Tọa độ C là trung điểm của AB là
A. C = (4; 6);
B. C = (5; 6);
C. C = (4; 5);
Câu 5:
Trong mặt phẳng tọa độ Oxy cho ba điểm A(3; 6), B(6; 9) và C(9; 12). Tọa độ trọng tâm của tam giác ABC là
A. G(6; 6);
B. G(6; 9);
C. G(9; 12);
Câu 7:
Trong mặt phẳng tọa độ Oxy cho và . Biết Xác định vị trí tương đối giữa và .
A. và cùng phương;
B. và cùng hướng;
C. và ngược hướng;
Câu 1:
Trong mặt phẳng tọa độ Oxy cho và . Tọa độ của vectơ là:
A. (7; –12);
B. (7; 12);
C. (1; –12);
Câu 2:
Trong mặt phẳng tọa độ Oxy cho 4 điểm A(1; 2), B(2; 3), C(1; ‒1) và D(4; 5). Khẳng định nào là đúng?
A. và cùng hướng;
B. và ngược hướng;
C. và vuông góc với nhau;
Câu 3:
Trong mặt phẳng tọa độ Oxy cho tam giác ABC. Biết A(1; 3); B(2; 4) và C(5; 3). Tính góc giữa 2 vectơ .
A. ;
B. ;
C. ;
Câu 4:
Trong mặt phẳng tọa độ Oxy cho 2 điểm A(2; 4) và B(4; 5). Tọa độ điểm D thỏa mãn là:
A. D = (2; 3);
B. D = (6; 6);
C. D = (4; 6);
Câu 5:
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(2; 5), B(4; 2) và C(5; 1). Tọa độ điểm D thỏa mãn ABDC là hình bình hành là
A. D(2; 3);
B. D(1; 3);
C. D(7; ‒2);
Câu 6:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC, biết A(1; 2), B(2; 4), C(4; 2). Chu vi tam giác ABC là
A. ;
B. P = 10;
C. ;
Câu 7:
Trong mặt phẳng tọa độ Oxy, cho hai vectơ và Giá trị của k để vectơ và vectơ có độ dài bằng nhau là:
A.
B.
C.
Câu 8:
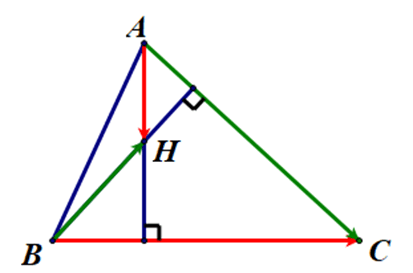
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(4; 3), B(2; 7) và C(– 3; –8). Tọa độ chân đường cao H kẻ từ A xuống cạnh BC là:
A. H(1; –4);
B. H(–1; 4);
C. H(1; 4);
Câu 1:
Một con tàu đang xuôi dòng có chiều cùng chiều với tia Ox của hệ tọa độ Oxy với vận tốc . Cho biết vận tốc của dòng nước là . Tìm tọa độ vectơ là tổng 2 vectơ và .
A. ;
B. ;
C. ;
Câu 2:
Trong mặt phẳng tọa độ Oxy, gọi H là chân đường cao hạ từ A xuống BC của tam giác ABC. G là trọng tâm tam giác ABC. Tính độ dài đoạn GH, biết A(1; 4), B(2; 5), C(5; 2).
A. GH = 3;
B. GH = ;
C. GH = ;
Câu 3:
Trong mặt phẳng tọa độ Oxy cho hình thoi ABCD có A(2; 3), B(3; 5). Gọi I là tâm hình thoi ABCD, G là trọng tâm tam giác ICD. Tính độ dài đoạn thẳng CG biết I trùng với gốc tọa độ O.
A. CG = 2;
B. ;
C. CG = 3;
Câu 4:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; –1) và B(3; 2). Tọa độ điểm M thuộc trục tung sao cho MA2 + MB2 nhỏ nhất là:
A. M(0; 1);
B. M(0; –1);
C.
Câu 5:
Hai con tàu cùng rời cảng và đi theo hai hướng khác nhau. Chọn hệ trục tọa độ sao cho bến cảng là gốc tọa độ. Khi đó quãng đường đi được và hướng của tàu thứ nhất và thứ hai được biểu thị bởi hai vectơ như hình dưới đây (độ dài một đơn vị trên trục tương ứng với 100 m trên thực tế).
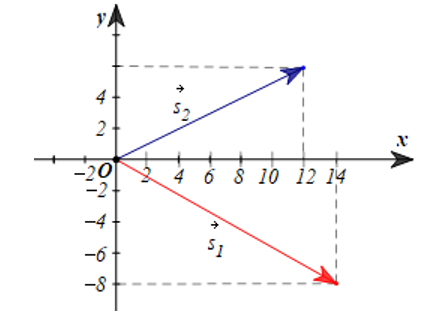
Hỏi quãng đường tàu thứ nhất đi được dài hơn tàu thứ hai bao nhiêu mét? Khoảng cách giữa hai tàu là bao nhiêu mét? (kết quả làm tròn đến hàng phần trăm).
A. 347,54 m và 1 216,55 m;
B. 1 216,55 m và 347,50 m;
C. 347,54 m và 2 877,36 m;