15 Bài tập Khái niệm vectơ Trắc nghiệm Toán 10 (có đáp án) - Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Khái niệm vectơ Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Chân trời sáng tạo sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.

15 Bài tập Khái niệm vectơ Trắc nghiệm Toán 10 (có đáp án) - Chân trời sáng tạo

Câu 1. Nếu $\overrightarrow{AB}=\overrightarrow{AC}$ thì

A. Tam giác ABC là tam giác cân;

B. Tam giác ABC là tam giác đều;

C. A là trung điểm của đoạn thẳng BC;

D. Điểm B trùng với điểm C.

Hiển thị đáp án

Đáp án đúng là: D

$\overrightarrow{AB}=\overrightarrow{AC}$ ⇒ AB = AC và hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng phương.

Do đó: A, B, C là ba điểm thẳng hàng và B, C nằm cùng phía so với A.

Mà AB = AC nên B ≡ C.

Câu 2. Cho tam giác ABC, có thể xác định được bao nhiêu vectơ khác vectơ-không có điểm đầu và điểm cuối là các đỉnh A, B, C?

A. 4;

B. 6;

C. 9;

D. 12.

Hiển thị đáp án

Đáp án đúng là: B

Vectơ-không là vectơ có điểm đầu và điểm cuối trùng nhau.

Vectơ khác vectơ-không là vectơ có điểm đầu khác điểm cuối.

Các vectơ khác vectơ-không có điểm đầu và điểm cuối là các đỉnh A, B, C là: $\overrightarrow{AB},\overrightarrow{BA},\overrightarrow{BC},\overrightarrow{CB},\overrightarrow{CA},\overrightarrow{AC}$.

Do đó có 6 vectơ thỏa mãn yêu cầu bài toán.

Câu 3. Cho hai vectơ không cùng phương $\overrightarrow{a}$ và $\overrightarrow{b}$. Mệnh đề nào sau đây đúng?

A. Không có vectơ nào cùng phương với cả hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$;

B. Có vô số vectơ cùng phương với cả hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$;

C. Có một vectơ cùng phương với cả hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$, đó là $\overrightarrow{0}$;

D. Cả A, B, C đều sai.

Hiển thị đáp án

Đáp án đúng là: C

Vì $\overrightarrow{0}$ cùng phương với mọi vectơ nên có một vectơ cùng phương với cả hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ đó là $\overrightarrow{0}$.

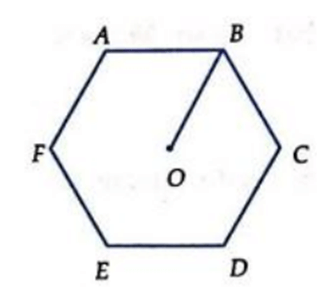
Câu 4. Cho hình lục giác đều ABCDEF tâm O. Số các vectơ khác vectơ-không, cùng phương với $\overrightarrow{OB}$, có điểm đầu và điểm cuối đều là các đỉnh của lục giác là:

A. 4;

B. 6;

C. 8;

D. 10.

Hiển thị đáp án

Đáp án đúng là: B

Các vectơ cùng phương với $\overrightarrow{OB}$ nếu chúng có giá song song hoặc trùng nhau.

Do đó các vectơ cùng phương với $\overrightarrow{OB}$ có điểm đầu và cuối là các đỉnh của lục giác là: $\overrightarrow{BE},\overrightarrow{EB},\overrightarrow{DC},\overrightarrow{CD},\overrightarrow{FA},\overrightarrow{AF}$.

Do đó có 6 vectơ thỏa mãn yêu cầu bài toán.

Câu 5. Cho hình vuông ABCD, khẳng định nào sau đây là đúng?

A. $\overrightarrow{AB}=\overrightarrow{BC}$;

B. $\overrightarrow{AB}=\overrightarrow{CD}$;

C. $\overrightarrow{AC}=\overrightarrow{BD}$;

D. $\left(\overrightarrow{AD}\right)=\left(\overrightarrow{CB}\right)$.

Hiển thị đáp án

Đáp án đúng là: D

Các cặp vectơ ở đáp án A, B, C không cùng hướng nên ta loại 3 đáp án này.

Vì ABCD là hình vuông nên AD = CB ⇔ $\left(\overrightarrow{AD}\right)=\left(\overrightarrow{CB}\right)$.

Do đó ta chọn đáp án D.

Câu 6. Cho $\overrightarrow{AB}$ và một điểm C. Có bao nhiêu điểm D thỏa mãn $\overrightarrow{AB}=\overrightarrow{CD}$

A. 1;

B. 2;

C. 0;

D. Vô số.

Hiển thị đáp án

Đáp án đúng là: A

Có một và chỉ một điểm D thỏa mãn $\overrightarrow{AB}=\overrightarrow{CD}$.

Câu 7. Hai vectơ được gọi là bằng nhau khi và chỉ khi

A. Giá của chúng trùng nhau và độ dài của chúng bằng nhau;

B. Chúng trùng với một trong các cặp cạnh đối của một hình bình hành;

C. Chúng trùng với một trong các cặp cạnh đối của một tam giác đều;

D. Chúng có cùng hướng và độ dài của chúng bằng nhau.

Hiển thị đáp án

Đáp án đúng là: D

Hai vectơ được gọi là bằng nhau nếu chúng có cùng hướng và có cùng độ dài.

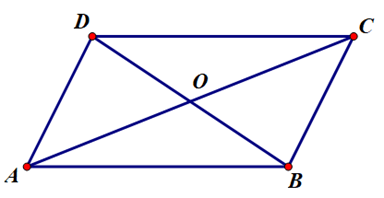
Câu 8. Cho hình bình hành ABCD với O là giao điểm của hai đường chéo. Khẳng định nào sau đây là sai?

A. $\overrightarrow{AB}=\overrightarrow{CD}$;

B. $\overrightarrow{AD}=\overrightarrow{BC}$;

C. $\overrightarrow{AO}=\overrightarrow{OC}$;

D. $\overrightarrow{OD}=\overrightarrow{BO}$.

Hiển thị đáp án

Đáp án đúng là: A

Hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ được gọi là đối nhau nếu chúng ngược hướng và có cùng độ dài.

Vì ABCD là hình bình hành nên AB = CD hay $\left(\overrightarrow{AB}\right)=\left(\overrightarrow{CD}\right)$.

Mà hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{CD}$ là hai vectơ ngược hướng với nhau.

Do đó $\overrightarrow{AB}$ và $\overrightarrow{CD}$ là hai vectơ đối nhau.

Vậy ta chọn đáp án A.

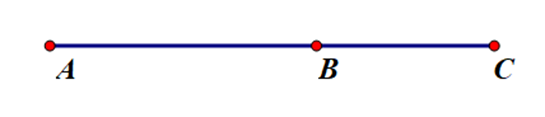
Câu 9. Cho ba điểm A, B, C cùng nằm trên một đường thẳng. Các vectơ $\overrightarrow{AB},\overrightarrow{BC}$ cùng hướng khi và chỉ khi

A. Điểm B thuộc đoạn AC;

B. Điểm A thuộc đoạn BC;

C. Điểm C thuộc đoạn AB;

D. Điểm B nằm ngoài đoạn AC.

Hiển thị đáp án

Đáp án đúng là: A

Các vectơ $\overrightarrow{AB},\overrightarrow{BC}$ cùng hướng khi và chỉ khi điểm B thuộc đoạn AC.

Câu 10. Cho tam giác ABC đều cạnh 2a. Đẳng thức nào sau đây là đúng?

A. $\overrightarrow{AB}=\overrightarrow{AC}$;

B. $\overrightarrow{AB}=2a$;

C. $\left(\overrightarrow{AB}\right)=2a$;

D. $\overrightarrow{AB}=AB$.

Hiển thị đáp án

Đáp án đúng là: C

Vì tam giác ABC đều cạnh 2a nên $\left(\overrightarrow{AB}\right)=AB=2a$.

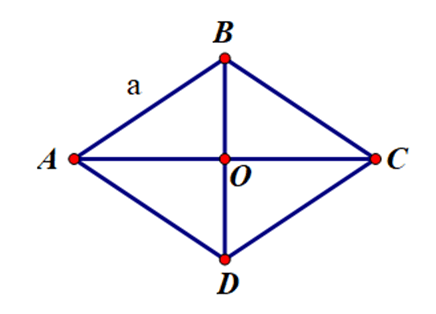
Câu 11. Cho hình thoi ABCD tâm O, cạnh bằng a và $\hat{A}=60°$. Kết luận nào sau đây là đúng?

A. $\left(\overrightarrow{AO}\right)=\frac{a\sqrt{3}}{2}$;

B. $\left(\overrightarrow{OA}\right)=a$;

C. $\left(\overrightarrow{OA}\right)=\left(\overrightarrow{OB}\right)$;

D. $\left(\overrightarrow{AO}\right)=\frac{a\sqrt{2}}{2}$.

Hiển thị đáp án

Đáp án đúng là: A

Vì ABCD là hình thoi nên AB = AD.

Do đó tam giác ABD cân tại A.

Mà tam giác ABD có $\hat{A}=60°$.

Do đó tam giác ABD là tam giác đều.

Tam giác ABD đều cạnh bằng a có AO là đường trung tuyến (vì O là tâm của hình thoi ABCD nên O là trung điểm BD).

Suy ra AO cũng là đường cao của tam giác ABD.

Vì O là trung điểm BD nên BO = $\frac{BD}{2}=\frac{a}{2}$.

Tam giác ABO vuông tại O: AO² = AB² – BO² (Định lý Pytago)

$\iff A{O}^2=a^2-{\left(\frac{a}{2}\right)}^2=\frac{3a^2}{4}$.

$\Rightarrow AO=\frac{a\sqrt{3}}{2}$.

$\Rightarrow \left(\overrightarrow{AO}\right)=\frac{a\sqrt{3}}{2}$.

Do đó ta chọn đáp án A.

Câu 12. Cho $\overrightarrow{MN}\ne \overrightarrow{0}$ thì số vectơ cùng phương với vectơ đã cho là

A. 1;

B. 2;

C. 3;

D. Vô số.

Hiển thị đáp án

Đáp án đúng là: D

Hai vectơ được gọi là cùng phương nếu giá của chúng song song hoặc trùng nhau.

Giá của vectơ $\overrightarrow{MN}\ne \overrightarrow{0}$ là đường thẳng MN, mà ta có vô số đường thẳng song song và trùng với MN.

Do đó có vô số vectơ cùng phương với $\overrightarrow{MN}\ne \overrightarrow{0}$.

Câu 13. Cho hình chữ nhật ABCD có AB = 5cm, BC = 12cm. Độ dài của $\overrightarrow{AC}$ là

A. 4cm;

B. 6cm;

C. 8cm;

D. 13cm.

Hiển thị đáp án

Đáp án đúng là: D

Vì ABCD là hình chữ nhật nên $\hat{B}=90°$.

Tam giác ABC vuông tại B: AC² = AB² + BC² (Định lý Pytago)

⇔ AC² = 5² + 12² = 169.

⇒ AC = 13 (cm).

Do đó $\left(\overrightarrow{AC}\right)=AC=13\left(cm\right)$.

Vậy ta chọn đáp án D.

Câu 14. Mệnh đề nào sau đây là đúng?

A. Có duy nhất một vectơ cùng phương với mọi vectơ;

B. Có ít nhất hai vectơ cùng phương với mọi vectơ;

C. Có vô số vectơ cùng phương với mọi vectơ;

D. Không có vectơ nào cùng phương với mọi vectơ.

Hiển thị đáp án

Đáp án đúng là: A

Chỉ có vectơ-không cùng phương với mọi vectơ.

Nên có duy nhất một vectơ cùng phương với mọi vectơ.

Câu 15. Mệnh đề nào sau đây sai?

A. $\overrightarrow{\text{AA}}=\overrightarrow{0}$;

B. $\overrightarrow{0}$ cùng hướng với mọi vectơ;

C. $\left(\overrightarrow{AB}\right)>0$;

D. $\overrightarrow{0}$ cùng phương với mọi vectơ.

Hiển thị đáp án

Đáp án đúng là: C

Vì có thể xảy ra trường hợp $\left(\overrightarrow{AB}\right)=0\iff A\equiv B$.