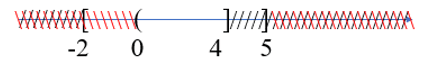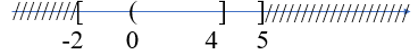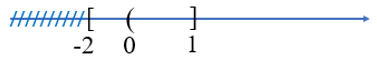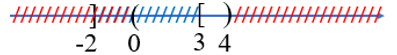15 Bài tập Tập hợp. Các phép toán trên tập hợp (có đáp án) - Cánh diều Trắc nghiệm Toán 10
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Tập hợp. Các phép toán trên tập hợp Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
15 Bài tập Tập hợp. Các phép toán trên tập hợp (có đáp án) - Cánh diều Trắc nghiệm Toán 10
Câu 1. Xác định tập hợp bằng cách liệt kê các phần tử.
A. B = {–2; –1; 1; 2};
B. B = {0; 1; 2};
C. B = {–2; –1; 0; 1; 2};
D. B = {–1; 0; 1; 2}.
Câu 2. Cho A = {x ∈ | x ≤ 5}. Tập A là tập hợp nào trong các tập sau:
A. {1; 2; 3; 4; 5};
B. {0; 1; 2; 3; 4};
C. {0; 1; 2; 3; 4; 5};
D. {1; 2; 3; 4}.
Câu 3. Hình vẽ dưới đây biểu diễn tập hợp nào ?
A. (–3; 2);
B.[–3; 2);
C.[–3; 2];
D.(–3; 2].
Câu 4. Cho tập hợp A ≠ ∅. Trong các mệnh đề sau, mệnh đề nào SAI?
A. A ∩ A = A;
B. A ∩ ∅ = A;
C. A \ A = ∅;
D. A ∪ ∅ = A.
Câu 5. Trong các đáp án dưới đây, cách viết khác của tập D = {x ∈ ℝ | x ≠ -3} là
A. ℝ \ {-3};
B. (–3; +∞);
C. (−∞; −3);
D. {−3}.
Câu 6. Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp .
A. [–3; 5);
B. [–3; 5];
C. (–3; 5);
D. (–3; 5].
Câu 7. Cho tập hợp A = (−∞; 4] và B = [−2; +∞). Xác định tập hợp A ∩ B?
A. [−2; 4];
B. (−2; 4];
C. [−2; 4);
D. .
Câu 8. Cho A = [−2; 4] và B = (0; 5]. Khẳng định nào sau đây là SAI?
A. A ∪ B = [−2; 5];
B. A ∩ B = [0; 4];
C. A \ B = [−2; 0];
D. B \ A = (4 ; 5].
Câu 9. Cho A = [−7; +∞). Tập hợp là:
A. (−∞; −7);
B. (−∞; −7];
C. (−7; +∞);
D. [−7; +∞).
Câu 10. Cho A = {1; 3; 4; 7} và B = {3; 5; 7; 10} . Tập A\ B là:
A. {1; 4};
B. {3; 7};
C. {5; 10};
D. ∅.
Câu 11. Cho hai tập A = [−2; 1] và B = (0; +∞). Tập hợp A ∪ B là:
A. [1; +∞);
B. [−2;0];
C. (0; 1];
D. [−2; +∞).
Câu 12. Cho hai tập A = [−2; 1] và B = (0; +∞). Tập hợp B \ A là:
A. (1; +∞);
B. [1; +∞);
C. [−2; 0];
D. [−2; 0).
Câu 13. Cho A = (−∞;−2], B = [3; +∞) và C = (0; 4). Khi đó, (A ∪ B) ∩ C là:
A. [3; 4];
B. (−∞; −2] ∪ (3; +∞);
C. [3; 4);
D. (−∞; −2) ∪ [3; +∞).
Câu 14. Cho A = {a, b}. Số tập con của A là:
A. 1;
B. 2;
C. 3;
D. 4.
Câu 15. Cho A = {0; 1; 2}. Số tập con của A là:
A. 5;
B. 6;
C. 7;
D. 8.
Câu 1:
Xác định tập hợp bằng cách liệt kê các phần tử.
B. B = {0; 1; 2};
Câu 2:
Câu 3:
Hình vẽ dưới đây biểu diễn tập hợp nào?

Câu 4:
Cho tập hợp A ¹ Æ. Trong các mệnh đề sau, mệnh đề nào SAI?
Câu 5:
Trong các đáp án dưới đây, cách viết khác của tập là
Câu 6:
Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp .
Câu 7:
Cho tập hợp A = (−∞; 4] và B = [−2; +∞). Xác định tập hợp A ∩ B?
Câu 8:
Cho A = [−2; 4] và B = (0; 5]. Khẳng định nào sau đây là SAI?
Câu 9:
Cho A = [−7; +∞). Tập hợp là:
Câu 10:
Cho A = {1; 3; 4; 7} và B = {3; 5; 7; 10} . Tập A\ B là:
Câu 11:
Cho hai tập A = [−2; 1] và B = (0; +∞). Tập hợp A ∪ B là:
Câu 12:
Cho hai tập A = [−2; 1] và B = (0; +∞). Tập hợp B \ A là:
Câu 13:
Cho A = (−∞;−2], B = [3; +∞) và C = (0; 4). Khi đó, (A ∪ B) ∩ C là:
Câu 1:
Cho tập hợp A như sau:
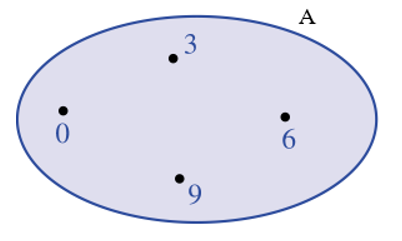
Khẳng định nào sau đây sai?
Câu 2:
Cho tập hợp B. Mệnh đề nào sau đây là mệnh đề đúng?
Câu 4:
Sử dụng các kí hiệu đoạn, khoảng, nửa khoảng để viết tập hợp
M = {x ∈ ℝ| 5 < x ≤ 10}.
B. M = (5; 10];
Câu 5:
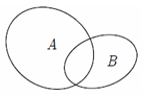
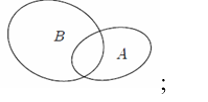
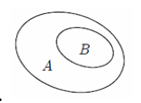
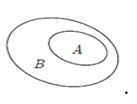
Phần không bị gạch trên hình vẽ dưới đây minh họa cho tập hợp nào?
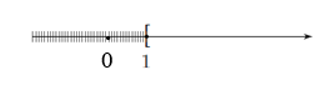
Câu 6:
Cho tập hợp H = {a; b; c; d; e}. Số phần tử của tập hợp H là:
A. 1
B. 3
C. 5
Câu 7:
Kí hiệu nào sau đây để chỉ – 2 là số nguyên?
Câu 1:
Liệt kê các phần tử của tập hợp E = {x ∈ ℕ| 2x2 – 3x + 1 = 0}:
C. \(E = \left\{ {\frac{1}{2}} \right\}\);
Câu 2:
Cho tập hợp A = {1; 3; 5; 7}. Tập hợp A có bao nhiêu tập con có hai phần tử?
A. 6
B. 8
C. 9
D. 16
Câu 3:
Cho các tập hợp A = {1; 5}, B = {1; 3; 5}. Chọn kết quả đúng trong các kết quả sau:
Câu 4:
Cho tập hợp C = [–5; 3), D = (1; +∞). Khi đó C ∩ D là tập nào sau đây?
Câu 5:
Cho A = (– ∞; – 2], B = [3; + ∞), C = (0; 4). Khi đó tập (A ∪ B) ∩ C là:
Câu 6:
Cho hai tập hợp A = {x ∈ ℤ| (x2 – 10x + 21)(x3 – x) = 0}, B = {x ∈ ℤ| – 3 < 2x + 1 < 5}. Khi đó tập X = A \ B là:
Câu 7:
Cho hai tập hợp A = {1; 2; 4; 6} và B = {1; 2; 3; 4; 5; 6; 7; 8}. Xác định tập CBA.
Câu 8:
Cho tập hợp H = (– ∞; 3) ∪ [9; + ∞). Hãy viết lại tập hợp H dưới dạng nêu tính chất đặc trưng.
Câu 1:
Cho tập hợp C = {x ∈ ℝ| 8 < |– 3x + 5|}. Hãy viết lại các tập hợp C dưới dạng khoảng, nửa khoảng, đoạn.
Câu 2:
Cho tập hợp \({C_\mathbb{R}}A = \left[ {0;6} \right)\), \({C_\mathbb{R}}B = \left( { - \frac{{12}}{3};5} \right) \cup \left( {\sqrt {17} ;\sqrt {55} } \right).\) Tập \({C_\mathbb{R}}\left( {A \cap B} \right)\)là:
A. \[\left[ { - \frac{{12}}{3};\sqrt {55} } \right]\];
D. \(\left( { - \frac{{12}}{3};0} \right) \cup \left( {\sqrt {17} ;\sqrt {55} } \right)\).
Câu 3:
Một lớp học có 23 học sinh giỏi môn Toán, 22 học sinh giỏi môn Lý, 15 học sinh
giỏi cả môn Toán và Lý và có 5 học sinh không giỏi môn nào cả. Hỏi lớp đó có bao nhiêu học sinh?
A. 35
B. 40
C. 45
D. 50
Câu 4:
Cho A = {x ∈ ℝ| x + 2 ≥ 0}, B = {x ∈ ℝ| 5 – x ≥ 0}. Số các số nguyên thuộc cả hai tập A và B là:
A. 6
B. 8
C. 5
D. 3
Câu 5:
Cho hai tập khác rỗng E = (m – 1; 4] và F = (– 2; 2m + 2] với m ∈ ℝ. Xác định m để F ⊂ E.