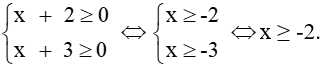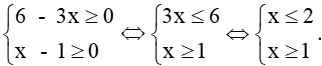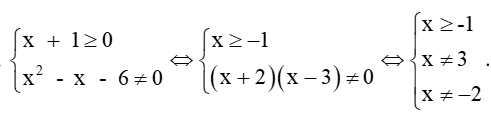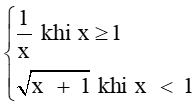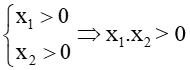15 Bài tập Hàm số và đồ thị (có đáp án) - Cánh diều Trắc nghiệm Toán 10
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Hàm số và đồ thị Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
15 Bài tập Hàm số và đồ thị (có đáp án) - Cánh diều Trắc nghiệm Toán 10
Câu 1 . Điểm nào sau đây thuộc đồ thị hàm số y = 4x + 1
A. (2; 3);
B. (0; 1);
C. (4; 5);
D. (0; 0).
Hiển thị đáp án
Đáp án đúng là: B
- Thay x = 2; y = 3 vào hàm số ta được: 3 = 4.1 + 1 (vô lí). Do đó, (2; 3) không thuộc đồ thị hàm số.
- Thay x = 0; y = 1 vào hàm số ta được: 1 = 0.1 + 1 (luôn đúng). Do đó, (0; 1) thuộc đồ thị hàm số.
- Thay x = 4; y = 5 vào hàm số ta được: 5 = 4.4 + 1 (vô lí). Do đó, (4; 5) không thuộc đồ thị hàm số.
- Thay x = 0; y = 0 vào hàm số ta được: 0 = 4.0 + 1 (vô lí). Do đó, (0; 0) không thuộc đồ thị hàm số.
Câu 2 . Cho hàm số y = f(x) =
A. f(2) = 10;
B. f(-1) = 10;
C. f(-2) = 1;
D. f(1) = 10.
Hiển thị đáp án
Đáp án đúng là: A
Thay lần lượt các giá trị: 2; (-1); (-2); 1 vào biểu thức
Ta được: Khi x = 2 thay vào hàm số y:
Câu 3 . Tập xác định của hàm số y = 3 x − 1 2 x − 2
A. D = ℝ
B. D = (1; 0);
C. D = (-∞; 1);
D. D = ℝ
Hiển thị đáp án
Đáp án đúng là: D
Hàm số y = 3 x − 1 2 x − 2 ⇔ 2 x ≠ 2 ⇔ x ≠ 1
Như vậy tập xác định của hàm số là
D = ℝ
Câu 4 . Tập xác định của hàm số y = x + 2
A. D =ℝ
B. D = (0; 2);
C. D = (-∞; 2];
D. D = [-2; +∞).
Hiển thị đáp án
Đáp án đúng là: D
Hàm số y = x + 2 ⇒
Câu 5. Tìm tập xác định của hàm số y = x + 2 − x + 3
A. D = [-3; +∞);
B. D = [-2; +∞);
C. D =ℝ
D. D = [2; +∞).
Hiển thị đáp án
Đáp án đúng là: B
Để hàm số y xác định thì
Tập xác định D = [-2; +∞)
Câu 6. Tìm tập xác định của y = 6 - 3 x − x - 1
A. D = (1; 2);
B. D = [1; 2];
C. D = [1; 3];
D. D = [-1; 2];
Hiển thị đáp án
Đáp án đúng là: B
Để hàm số y xác định thì
Tập xác định: D = [1; 2]
Câu 7. Tìm tập xác định của hàm số y = x + 1 x 2 - x - 6
A. D = {3};
B. D = [-1; +∞)\{3};
C. D = ℝ
D. D = [-1; +∞).
Hiển thị đáp án
Đáp án đúng là: B
Để hàm số y xác định thì
Tập xác định: D = [-1; +∞)\{3}
Câu 8 . Tìm tập xác định của hàm số y = f(x) =
A. D = {-1};
B. D = ℝ
C. D = [-1; +∞);
D. D = [-1; 1).
Hiển thị đáp án
Đáp án đúng là: C
Với x≥ 1 x ≥
Với x < 1 thì f(x) = x + 1 ≥ 0 ⇔ x ≥ − 1 x + 1 − 1 ≤ x < 1
Kết hợp (1) và (2) ta được f(x) xác định với mọi x ≥ + ∞
Câu 9 . Cho hàm số f(x) = 4 - 3x. Khẳng định nào sau đây sai?
A. Hàm số nghịch biến trên − ∞ ; 4 3
B. Hàm số nghịch biến trên 4 3 ; + ∞
C. Hàm số nghịch biến trên ℝ
D. Hàm số đồng biến trên 3 4 ; + ∞
Hiển thị đáp án
Đáp án đúng là: D
Bảng biến thiên
a = -3 < 0, hàm số nghịch biến trên R.
Câu 10 . Xét sự biến thiên của hàm số y = 3 x
A. Hàm số đồng biến trên (0; +∞);
B. Hàm số nghịch biến trên (0; +∞);
C. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng (0; +∞);
D. Hàm số không đồng biến, cũng không nghịch biến trên khoảng (0; +∞).
Hiển thị đáp án
Đáp án đúng là: B
Với x 1 ≠ x 2 f ( x 1 ) − f ( x 2 ) = 3 x 1 − 3 x 2 = 3 ( x 2 − x 1 ) x 1 x 2 = − 3 ( x 1 − x 2 ) x 1 x 2
Với mọi x 1 , x 2 ∈ x 1 < x 2
⇒ f ( x 1 ) − f ( x 2 ) x 1 − x 2 = − 3 ( x 1 − x 2 ) x 1 x 2 : x 1 − x 2 1 = − 3 x 1 x 2 x 1 . x 2
⇒ f ( x 1 ) − f ( x 2 ) x 1 − x 2 = − 3 ( x 1 − x 2 ) x 1 x 2 : x 1 − x 2 1 = − 3 x 1 x 2 x 1 . x 2 − 3 x 1 x 2
⇒ 3 x
Câu 11 . Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để hàm số f(x) = (m + 1)x + m - 2 đồng biến trên ℝ
A. 7;
B. 5;
C. 4;
D. 3.
Hiển thị đáp án
Đáp án đúng là: C
Tập xác định: D = ℝ
Ta có y = (m + 1)x + m – 2 đồng biến khi m + 1 > 0<⇔
Với m∈ ∈
Câu 12 . Tìm tham số m để hàm số y = f(x) = -x 2
A. m < 5;
B. m > 5;
C. m < 3;
D. m >3.
Hiển thị đáp án
Đáp án đúng là: C
Với mọi x 1 ≠ x 2
f(x 1 ) - f(x 2 ) x 1 - x 2 = [-x 1 2 + (m + 1)x 1 + 2] - [-x 2 2 + (m + 1)x 2 + 2] x 1 - x 2 -(x 1 + x 2 ) + m - 1
Để hàm số nghịch biến trên (1; 2) ⇔ -(x 1 + x 2 ) + m - 1 x 1 x 2 ∈
m < (x 1 + x 2 ) x 1 x 2 ∈ ⇔
Câu 13 . Điểm nào không thuộc đồ thị hàm số đồ thị y = f(x) = 5x - 1
A. (0; -1);
B. (1; 4);
C. (2; 9);
D. (1; 2).
Hiển thị đáp án
Đáp án đúng là: D
- Thay x = 0 vào hàm số y = 5x - 1 ta được: -1 = 5.0 - 1 (Đúng). Như vậy điểm (0; -1) thuộc đồ thị.
- Thay x = 1 vào hàm số y = 5x - 1 ta được: 4 = 5.1 -1 (Đúng). Như vậy điểm (1; 4) thuộc đồ thị.
- Thay x =2 vào hàm số y = 5x - 1 ta được: 9 = 5.2 - 1 (Đúng). Như vậy điểm (2; 9) thuộc đồ thị.
Như vậy điểm (1; 2) không thuộc đồ thị hàm số y = 5x - 1.
Câu 14. Tìm m để hàm số y = f(x) = x x - m
A. 0 < m < 5;
B. m ≤ 0;
C. m ≥ 5;
D. m ≤ 0 hoặc m ≥ 5.
Hiển thị đáp án
Đáp án đúng là: D
Hàm số y xác định khi x - m ≠ 0⇔ ∉
Câu 15. Tìm m để hàm số y = m x + 2
A. m > 0;
B. m < 0;
C. m = 0;
D. m > -2.
Hiển thị đáp án
Đáp án đúng là: A
Tập xác định: D = ℝ
Với x 1 ≠ x 2
f(x 2 ) - f(x 1 ) x 2 - x 1 = m x 2 + 2 - m x 1 + 2 x 2 - x 1 = m ( x 1 + 2 ) − m ( x 2 + 2 ) ( x 1 + 2 ) ( x 2 + 2 ) x 2 − x 1
= m x 1 + 2 m − m x 2 − 2 m ( x 1 + 2 ) ( x 2 + 2 ) x 2 − x 1
= - m ( x 2 − x 1 ) ( x 1 + 2 ) ( x 2 + 2 ) : x 2 − x 1 1 = − m ( x 1 + 2 ) ( x 2 + 2 )
Với x 1 , x 2 ( x 2 + 2 ) ( x 1 + 2 ) f(x 2 ) - f(x 1 ) x 2 - x 1 ⇒
Câu 1:
Điểm nào sau đây thuộc đồ thị hàm số y = 4x + 1
A. (2; 3);
B. (0; 1);
C. (4; 5);
D. (0; 0).
Xem lời giải »
Câu 2:
Cho hàm số y = f(x) = 5 x . Khẳng định nào sau đây là đúng?
A. f(2) = 10;
B. f(-1) = 10;
C. f(-2) = 1;
D. f(1) = 10.
Xem lời giải »
Câu 3:
Tập xác định của hàm số y = 3 x − 1 2 x − 2 là:
A. D = ℝ ;
B. D = (1; 0);
C. D = (-∞; 1);
D. D = ℝ \{1}.
Xem lời giải »
Câu 4:
Tập xác định của hàm số y = x + 2 là:
A. D =ℝ \{-2};
B. D = (0; 2);
C. D = (-∞; 2];
D. D = [-2; +∞).
Xem lời giải »
Câu 5:
Tìm tập xác định của hàm số y = x + 2 − x + 3
A. D = [-3; +∞);
B. D = [-2; +∞);
C. D =ℝ ;
D. D = [2; +∞).
Xem lời giải »
Câu 6:
Tìm tập xác định của y = 6 - 3 x − x - 1
A. D = (1; 2);
B. D = [1; 2];
C. D = [1; 3];
D. D = [-1; 2];
Xem lời giải »
Câu 7:
Tìm tập xác định của hàm số y = x + 1 x 2 - x - 6
A. D = {3};
B. D = [-1; +∞)\{3};
C. D = ℝ ;
D. D = [-1; +∞).
Xem lời giải »
Câu 8:
Tìm tập xác định của hàm số y = f(x) = 1 x k h i x ≥ 1 x + 1 k h i x < 1
A. D = {-1};
B. D = ℝ ;
C. D = [-1; +∞);
D. D = [-1; 1).
Xem lời giải »
Câu 9:
Cho hàm số f(x) = 4 - 3x. Khẳng định nào sau đây sai?
A. Hàm số nghịch biến trên − ∞ ; 4 3
B. Hàm số nghịch biến trên 4 3 ; + ∞
C. Hàm số nghịch biến trên ℝ ;
D. Hàm số đồng biến trên 3 4 ; + ∞ .
Xem lời giải »
Câu 10:
Xét sự biến thiên của hàm số y = 3 x trên khoảng (0; +∞). Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên (0; +∞);
B. Hàm số nghịch biến trên (0; +∞);
C. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng (0; +∞);
D. Hàm số không đồng biến, cũng không nghịch biến trên khoảng (0; +∞).
Xem lời giải »
Câu 11:
Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để hàm số f(x) = (m + 1)x + m - 2 đồng biến trên ℝ .
A. 7
B. 5
C. 4
D. 3
Xem lời giải »
Câu 12:
Tìm tham số m để hàm số y = f(x) = -x 2 + (m - 1)x + 2 nghịch biến trên khoảng (1; 2).
A. m < 5;
B. m > 5;
C. m < 3;
D. m >3.
Xem lời giải »
Câu 13:
Điểm nào không thuộc đồ thị hàm số đồ thị y = f(x) = 5x - 1
A. (0; -1);
B. (1; 4);
C. (2; 9);
D. (1; 2).
Xem lời giải »
Câu 14:
Tìm m để hàm số y = f(x) = x x - m xác định trên khoảng (0; 5)
A. 0 < m < 5;
B. m ≤ 0;
C. m ≥ 5;
D. m ≤ 0 hoặc m ≥ 5.
Xem lời giải »
Câu 15:
Tìm m để hàm số y = m x + 2 luôn nghịch biến trong khoảng xác định của nó.
A. m > 0;
B. m < 0;
C. m = 0;
D. m > -2.
Xem lời giải »
Câu 1:
Cho hàm số y = f(x) xác định trên khoảng (a; b). Hàm số y = f(x) gọi là đồng biến trên khoảng (a; b) khi?
A. ∀ x1 , x2 Î (a; b), x1 < x2 Þ f(x1 ) < f(x2 );
B. ∀ x1 , x2 Î (a; b), x1 > x2 Þ f(x1 ) < f(x2 );
C. ∀ x1 , x2 Î (a; b), x1 = x2 Þ f(x1 ) < f(x2 );
D. ∀ x1 , x2 Î (a; b), x1 ≤ x2 Þ f(x1 ) < f(x2 ).
Xem lời giải »
Câu 2:
Cho hàm số y = f(x) xác định trên khoảng (a; b). Hàm số y = f(x) gọi là nghịch biến trên khoảng (a; b) khi?
A. ∀ x1 , x2 Î (a; b), x1 < x2 Þ f(x1 ) < f(x2 );
B. ∀ x1 , x2 Î (a; b), x1 < x2 Þ f(x1 ) > f(x2 );
C. ∀ x1 , x2 Î (a; b), x1 < x2 Þ f(x1 ) = f(x2 );
D. ∀ x1 , x2 Î (a; b), x1 < x2 Þ f(x1 ) ≤ f(x2 ).
Xem lời giải »
Câu 3:
Công thức nào sau đây không phải là hàm số?
A. y = x – 1;
B. y = x 2 + 1
C. y = 1 x
D. |y| = 5x.
Xem lời giải »
Câu 4:
Điểm nào sau đây thuộc đồ thị hàm số y = 3|x – 2| + 3|x| − 2?
A. (2; 4);
B. (1; −1);
C. (−2; −10);
D. (0; −4).
Xem lời giải »
Câu 5:
Cho hàm số y = f(x) = |−9x|. Khẳng định nào sau đây là sai?
A. f(−1) = 9;
B. f(2) = 18;
C. f(−2) = 18;
D. f1 9
Xem lời giải »
Câu 6:
Điểm nào sau đây thuộc đồ thị y = 1 x - 1
A. M1 (2; 1);
B. M2 (1; 1);
C. M3 (2; 0);
D. M4 (0; −2).
Xem lời giải »
Câu 7:
Điểm nào sau đây không thuộc đồ thị hàm số y = x 2 − 4 x + 4 x
A. A(2; 0);
B. B3 ; 1 3
C. C(1; −1);
D. D(−1; −3).
Xem lời giải »
Câu 1:
Xác định các hệ số của a và b để đồ thị của hàm số y = ax + b đi qua điểm M(1; 7) và N(0; 3).
A. a = 3, b = 4;
B. a = 4, b = 3;
C. a = 1 4 - 3 4
D. a = - 7 2 21 2
Xem lời giải »
Câu 2:
Cho đường thẳng d1: y = 1 2
A. y = - 1 2
B. y = - 1 2
C. y = 1 2
D. y = 1 2
Xem lời giải »
Câu 3:
Tập xác định của hàm số y = 3 − x , x ∈ − ∞ ; 0 1 x , x ∈ 0 ; + ∞
A. ℝ\ {0};
B. ℝ\ [0; 3];
C. ℝ\ {0; 3};
D. ℝ.
Xem lời giải »
Câu 4:
Tìm tập xác định của hàm số f(x) = 1 x ; x ≥ 1 x + 1 ; x < 1
A. D = {−1};
B. D = ℝ;
C. D = [−1; +∞
D. D = [−1; 1).
Xem lời giải »
Câu 5:
Tìm tất cả các giá trị thực của tham số m để hàm số y = 2 x + 1 x 2 − 6 x + m − 2
A. m ≥ 11;
B. m > 11;
C. m < 11;
D. m ≤ 11.
Xem lời giải »
Câu 6:
Cho hàm số bậc nhất y = ax + b. Tìm a và b, biết rằng đồ thị hàm số đi qua điểm M(−1; 1) và cắt trục hoành tại điểm có hoành độ là 5.
B. a = - 1 6 - 5 6
C. a = 1 6 - 5 6
D. a = - 1 6 5 6
Xem lời giải »
Câu 7:
Hàm số y = x + |x| được viết lại là:
A. y = x k h i x ≥ 0 2 x k h i x < 0
B. y = 0 k h i x ≥ 0 2 x k h i x < 0
C. y = 2 x k h i x ≥ 0 0 k h i x < 0
D. y = − 2 x k h i x ≥ 0 0 k h i x < 0
Xem lời giải »
Câu 8:
Tập xác định của hàm số y = 1 5 − x − x x − 2
A. ℝ;
B. (0; 5);
C. (2; 5);
D. (5; +∞
Xem lời giải »
Câu 1:
Tìm tất cả các giá trị thực của tham số m để hàm số y = x + 2 m + 2 x − m
A. m > 0 hoặc m < −1;
B. m ≤ −1;
C. m ≥ 0 hoặc m ≤ −1;
D. m ≥ 0.
Xem lời giải »
Câu 2:
Cho hàm số y = m x x − m + 2 − 1
A. m ∈ ∞ ∪
B. m ∈ ∞ ∪
C. m ∈ ∞ ∪
D. m ∈ ∞ ∪
Xem lời giải »
Câu 3:
Cho bốn đường thẳng:
(d1): y = x 3 + 1
(d2): y = 3 3 x − 1
(d3): y = − x 3 + 1
(d4): y = 3x + 2.
Hỏi cặp đường thẳng nào song song với nhau?
A. (d1 ) và (d2 );
B. (d2 ) và (d3 );
C. (d1 ) và (d3 );
D. (d2 ) và (d4 ).
Xem lời giải »
Câu 4:
Cho hai hàm số f(x) = 2x2 + 3x + 1 và g(x) = x 2 + 1 k h i x > 2 2 x − 1 k h i − 2 ≤ x ≤ 2 6 − 6 x k h i x < − 2 . Tìm x khi g(x) = 1.
A. x = 1;
B. x = 2;
C. x = 3;
D. x = 4.
Xem lời giải »
Câu 5:
Giá thuê xe ô tô tự lái là 1,4 triệu đồng một ngày cho hai ngày đầu tiên và 800 nghìn đồng cho mỗi ngày tiếp theo. Tổng số tiền T phải trả là một hàm số của số ngày x mà khách thuê xe. Viết công thức của hàm số T = T(x).
A. T(x) = 1,4 x ( 0 < x < 2 ) 0,8 x + 0,5 ( x > 2 )
B. T(x) = 1,2 x ( 0 < x ≤ 2 ) 0,8 x + 1,2 ( x > 2 )
C. T(x) = 1,4 x ( 0 < x ≤ 2 ) 0,8 x + 0,5 ( x > 2 )
D. T(x) = 1,4 x ( 0 < x ≤ 2 ) 0,8 x + 1,2 ( x > 2 )
Xem lời giải »

 .
.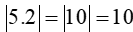 . (Chọn A)
. (Chọn A)