100 Bài tập trắc nghiệm Toán 10 Chương 7 (có đáp án): Phương pháp tọa độ trong mặt phẳng - Cánh diều
Haylamdo biên soạn và sưu tầm 200 bài tập trắc nghiệm Chương 7: Phương pháp tọa độ trong mặt phẳng Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
100 Bài tập trắc nghiệm Toán 10 Chương 7 (có đáp án): Phương pháp tọa độ trong mặt phẳng - Cánh diều
Câu 1:
Cho A (2; –4), B (–5; 3). Tìm tọa độ của \[\overrightarrow {AB} \].
A. (7; –7);
B. (–7; 7);
C. (9; –5);
D. (1; –5).
Xem lời giải »
Câu 2:
Cho C (3; –4), D (–1; 2). Biểu diễn vectơ \[\overrightarrow {CD} \] qua vectơ \(\overrightarrow i \) và vectơ \(\overrightarrow j \).
A. \( - 4\overrightarrow i + 6\overrightarrow j \);
B. \(2\overrightarrow i - 2\overrightarrow j \);
C. \(4\overrightarrow i - 6\overrightarrow j \);
D.\( - 3\overrightarrow i - 8\overrightarrow j \).
Xem lời giải »
Câu 3:
Tìm tọa độ của vectơ \[\overrightarrow {EF} \], biết \[\overrightarrow {EF} = 6\overrightarrow i - 9\overrightarrow j \]:
A. (6; –9);
B. (4; –5);
C. (6; 9) ;
D. (–5; –14).
Xem lời giải »
Câu 4:
Cho các vectơ sau: \[\overrightarrow a = 3\overrightarrow j \], \(\overrightarrow b \left( {0;3} \right)\), \(\overrightarrow c = 3\overrightarrow i \). Có bao nhiêu cặp vectơ bằng nhau:
A. 0;
B. 1;
C. 2;
D. 3.
Xem lời giải »
Câu 5:
Trong hệ tọa độ Oxy cho A (5; 2), B (10; 8). Tìm tọa độ của vectơ \[\overrightarrow {AB} \].
A. ;
B;
C. \[\overrightarrow {AB} \] = (5; 6);
D. \[\overrightarrow {AB} \] = (50; 16).
Xem lời giải »
Câu 6:
Trong hệ tọa độ Oxy cho ba điểm A (1; 3); B (–1; 2); C (–2 ; 1). Tìm tọa độ D sao cho tứ giác ABCD là hình chữ nhật.
A. (–2; 0);
B. (0; 2);
C. (–1; 2);
D. (–1; 0).
Xem lời giải »
Câu 7:
Trong hệ tọa độ Oxy cho hai điểm I (2; –3). Tìm tọa độ điểm M đối xứng với điểm I qua gốc O.
A. (2; 3);
B. (–2; –3);
C. (3; 2);
D. (–2; 3).
Xem lời giải »
Câu 8:
Trong hệ tọa độ Oxy cho ba điểm A(3; 5), B(1; 2), C(5; 2) và D(m ; n) . Tính m + n để ACDB là hình bình hành.
A. m + n = 3;
B. m + n = – 1;
C. m + n = 2;
D. m + n = 4.
Xem lời giải »
Câu 9:
Trong hệ tọa độ Oxy cho tam giác ABC có trọng tâm G (–1; 1). Tìm tọa độ điểm M đối xứng với G qua trục Oy.
A. (0; 1) ;
B. (–1; 0) ;
C. (–1; –1);
D. (1; 1).
Xem lời giải »
Câu 10:
Trong hệ tọa độ Oxy cho ba điểm A (–1 ; 1), B (1 ; 3), C (–1; 4) , D(1; 0). Khẳng định nào sau đây đúng?
A. \[\overrightarrow {BD} = \overrightarrow {AC} ;\]
B. \[\overrightarrow {AB} = \overrightarrow {CA} ;\]
C. \[\overrightarrow {DA} = \overrightarrow {BC} ;\]
D. \[\overrightarrow {CA} = \overrightarrow {BC} .\]
Xem lời giải »
Câu 11:
Trong hệ tọa độ Oxy cho bốn điểm A (3; -2), B (7; 1), C (0; 1), D (-8; -5) Khẳng định nào sau đây đúng?
A. \[\overrightarrow {AB} ,{\rm{ }}\overrightarrow {CD} \] là hai vectơ trùng nhau;
B. \[\overrightarrow {AB} ,{\rm{ }}\overrightarrow {CD} \] ngược hướng;
C. \[\overrightarrow {AB} ,{\rm{ }}\overrightarrow {CD} \] cùng hướng;
D. A, B, C, D trùng nhau.
Xem lời giải »
Câu 12:
Trong hệ tọa độ Oxy cho A (-1; 5), B (5; 5), C (-1; 11). Khẳng định nào sau đây đúng?
A. A, B, C trùng nhau ;
B. \[\overrightarrow {AB} ,{\rm{ }}\overrightarrow {AC} \] cùng phương ;
C. \[\overrightarrow {AB} ,{\rm{ }}\overrightarrow {AC} \] không cùng phương ;
D. \[\overrightarrow {AB} ,{\rm{ }}\overrightarrow {AC} \] bằng nhau.
Xem lời giải »
Câu 13:
Trong hệ tọa độ Oxy cho bốn điểm A(1; 1), B(2; -1), C(4 ; 3), D (3 ; 5) Khẳng định nào sau đây đúng?
A. Tứ giác ABCD là hình bình hành ;
B. A, B, C, D trùng nhau ;
C. \[\overrightarrow {AB} = \overrightarrow {CD} ;\]
D. \[\overrightarrow {AC} ,{\rm{ }}\overrightarrow {AD} \] cùng phương.
Xem lời giải »
Câu 14:
Trong hệ tọa độ Oxy cho tam giác ABC có A (1; 1), B (-2; -2), C (7; 7) Khẳng định nào sau đây đúng?
A. A, B, C thẳng hàng ;
B. B ở giữa hai điểm A và C ;
C. A ở giữa hai điểm B và C ;
D. \[\overrightarrow {AB} ,{\rm{ }}\overrightarrow {AC} \] cùng hướng.
Xem lời giải »
Câu 15:
Cho hai vectơ \[\overrightarrow u = \left( {2a - 1; - 3} \right)\] và \[\overrightarrow v = \left( {3;4b + 1} \right)\]. Tìm các số thực a và b sao cho cặp vectơ đã cho bằng nhau:
A. a = 2, b = – 1;
B. a = – 1, b = 2;
C. a = – 1, b = – 2;
D. a = 2, b = 1.
Xem lời giải »
Câu 1:
Trong mặt phẳng tọa độ Oxy, cho \(\overrightarrow {OA} = \left( {{a_1};{a_2}} \right)\). Khi đó hoành độ và tung độ của \(\overrightarrow {OA} \) lần lượt là:
A. a1 và a2;
B. a2 và a1;
C. \({a_1}\vec i\) và \({a_2}\vec j\);
D. –a1 và –a2.
Xem lời giải »
Câu 2:
Để xác định hoành độ của điểm K tùy ý trong mặt phẳng tọa độ Oxy, ta thực hiện như sau:
A. Kẻ một đường thẳng đi qua điểm K và vuông góc với trục Oy, đường thẳng này cắt trục Oy tại điểm K’’ ứng với số k2. Khi đó k2 là hoành độ của điểm K;
B. Kẻ một đường thẳng bất kì đi qua điểm K, đường thẳng này cắt trục Ox tại điểm K’ ứng với số k1. Khi đó k1 là hoành độ của điểm K;
C. Kẻ một đường thẳng đi qua điểm K và vuông góc với trục Ox, đường thẳng này cắt trục Ox tại điểm K’ ứng với số k1. Khi đó k1 là hoành độ của điểm K;
D. Vì K là điểm tùy ý nên ta có thể chọn hoành độ của điểm K tùy ý.
Xem lời giải »
Câu 3:
Trong mặt phẳng tọa độ Oxy, cho \(\vec u = \left( {2;7} \right)\). Kết luận nào sau đây đúng?
A. \(\vec u = 2\vec i - 7\vec j\);
B. \(\vec u = 7\vec i + 2\vec j\);
C. \(\vec u = 2\vec i + 7\vec j\);
D. \(\vec u = - 2\vec i - 7\vec j\).
Xem lời giải »
Câu 4:
Trong mặt phẳng tọa độ Oxy, cho G(3; 5). Tọa độ của \(\overrightarrow {OG} \) là:
A. (3; –5);
B. (5; 3);
C. (–3; –5);
D. (3; 5).
Xem lời giải »
Câu 5:
Trong mặt phẳng tọa độ Oxy, cho \(\vec u = \left( {{u_1};{u_2}} \right)\) và \(\vec v = \left( {{v_1};{v_2}} \right)\). Kết luận nào sau đây đúng?
A. \(\vec u = \vec v \Leftrightarrow \left\{ \begin{array}{l}{u_1} = {v_1}\\{u_2} = {v_2}\end{array} \right.\);
B. \(\vec u = - \vec v \Leftrightarrow \left\{ \begin{array}{l}{u_1} = {v_1}\\{u_2} = {v_2}\end{array} \right.\);
C. \(\vec u = \vec v \Leftrightarrow \left\{ \begin{array}{l}{u_1} = {v_2}\\{u_2} = {v_1}\end{array} \right.\);
D. \(\vec u = \vec v \Leftrightarrow \left\{ \begin{array}{l}{u_1} = - {v_1}\\{u_2} = - {v_2}\end{array} \right.\).
Xem lời giải »
Câu 6:
Vectơ đơn vị của trục Ox và trục Oy lần lượt là:
A.\(\vec i = \left( {0;1} \right),\,\,\vec j = \left( {1;0} \right)\);
B. \(\vec i = \left( {1;0} \right),\,\,\vec j = \left( {0;1} \right)\);
C. \(\vec j = \left( {1;0} \right),\,\,\vec i = \left( {0;1} \right)\);
D. \(\vec j = \left( {0;1} \right),\,\,\vec i = \left( {1;0} \right)\).
Xem lời giải »
Câu 7:
Trong mặt phẳng tọa độ Oxy, cho hai điểm \(M\left( {{x_M};{y_M}} \right)\) và \(N\left( {{x_N};{y_N}} \right)\). Khi đó ta có tọa độ \(\overrightarrow {MN} \) là:
A. \(\overrightarrow {MN} = \left( {{x_N} + {x_M};{y_N} + {y_M}} \right)\);
B. \(\overrightarrow {MN} = \left( {{x_M} - {x_N};{y_N} - {y_M}} \right)\);
C. \(\overrightarrow {MN} = \left( {{x_M} - {x_N};{y_M} - {y_N}} \right)\);
D. \(\overrightarrow {MN} = \left( {{x_N} - {x_M};{y_N} - {y_M}} \right)\).
Xem lời giải »
Câu 1:
Cho hình vẽ:
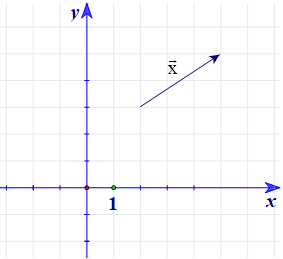
Tọa độ của \(\vec x\) là:
A. (5; 5);
B. (–3; –2);
C. (2; 3);
D. (3; 2).
Xem lời giải »
Câu 2:
Trong mặt phẳng tọa độ Oxy, cho hai điểm B(–1; 3) và C(5; 2). Tọa độ của \(\overrightarrow {BC} \) là:
A. \(\overrightarrow {BC} = \left( {6; - 1} \right)\);
B. \(\overrightarrow {BC} = \left( { - 6;1} \right)\);
C. \(\overrightarrow {BC} = \left( {4;5} \right)\);
D. \(\overrightarrow {BC} = \left( { - 6; - 1} \right)\).
Xem lời giải »
Câu 3:
Trong mặt phẳng tọa độ Oxy, cho ba điểm E (2; – 3), F(4; 7), G(1; 5). Nếu \(\overrightarrow {EF} = \overrightarrow {GH} \) thì tọa độ điểm H là:
A. H(15; 3);
B. H(7; 9);
C. H(3; 15);
D. H(5; –1).
Xem lời giải »
Câu 4:
Trong mặt phẳng tọa độ Oxy, cho \[\vec a = \left( {1;5} \right)\] và \(\vec b = \left( {3u + v;u - 2v} \right)\). Khi đó \(\vec a = \vec b\) khi và chỉ khi:
A. \(\left\{ \begin{array}{l}u = - 1\\v = 2\end{array} \right.\);
B. \(\left\{ \begin{array}{l}u = 1\\v = - 2\end{array} \right.\);
C. \(\left\{ \begin{array}{l}u = 1\\v = 2\end{array} \right.\);
D. \(\left\{ \begin{array}{l}u = - 1\\v = - 2\end{array} \right.\).
Xem lời giải »
Câu 5:
Trong mặt phẳng tọa độ Oxy, cho các điểm M(0; – 2), N(2; 4), P(– 5; 1), Q(– 3; 7). Cặp vectơ nào sau đây bằng nhau?
A. \(\overrightarrow {MP} \) và \(\overrightarrow {NQ} \);
B. \(\overrightarrow {MN} \) và \(\overrightarrow {QP} \);
C. \(\overrightarrow {MQ} \) và \(\overrightarrow {NP} \);
D. \(\overrightarrow {NM} \) và \(\overrightarrow {NP} \).
Xem lời giải »
Câu 6:
Trong mặt phẳng tọa độ Oxy, cho A(2; –3), B(4; 7). Tọa độ trung điểm I của đoạn thẳng AB là:
A. I(3; 2);
B. I(2; 10);
C. I(6; 4);
D. I(8; –21).
Xem lời giải »
Câu 7:
Trong mặt phẳng tọa độ Oxy, cho \[\vec g = \left( {2x;1 - 3y} \right)\] và \[\vec h = \left( {x - y;3y - x} \right)\]. Khi đó \(\vec g = \vec h\) khi và chỉ khi:
A. \(\left\{ \begin{array}{l}x = \frac{1}{7}\\y = - \frac{1}{7}\end{array} \right.\);
B. \(\left\{ \begin{array}{l}x = \frac{1}{3}\\y = \frac{1}{3}\end{array} \right.\);
C. \(\left\{ \begin{array}{l}x = - \frac{1}{7}\\y = \frac{1}{7}\end{array} \right.\);
D. \(\left\{ \begin{array}{l}x = 1\\y = 3\end{array} \right.\).
Xem lời giải »
Câu 8:
Cho điểm A(–2; 3) và \(\overrightarrow {AM} = 3\vec i - 2\vec j\).
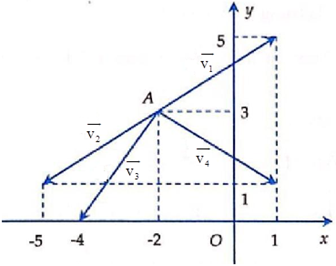
Vectơ nào trong hình là \(\overrightarrow {AM} \)?
A. \[\overrightarrow {{v_1}} \];
B. \[\overrightarrow {{v_2}} \];
C. \[\overrightarrow {{v_3}} \];
D. \(\overrightarrow {{v_4}} \).
Xem lời giải »
Câu 1:
Cho \(\vec u = \left( {{m^2} + 3;2m} \right)\), \(\vec v = \left( {5m - 3;{m^2}} \right)\). Nếu \(\vec u = \vec v\) thì m thuộc tập hợp:
A. {2};
B. {0; 2};
C. {0; 2; 3};
D. {3}.
Xem lời giải »
Câu 2:
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(4; – 1), B (7; 8). Tọa độ của điểm C là điểm đối xứng của A qua B là:
A. C(–4; 1);
B. C(4; –1);
C. C(–10; –17);
D. C(10; 17).
Xem lời giải »
Câu 3:
Trên mặt phẳng tọa độ Oxy, cho hai điểm A(1; –1), B(2; 4). Để tứ giác OBMA là hình bình hành thì tọa độ M là:
A. M(–3; –3);
B. M(3; –3);
C. M(3; 3);
D. M(–3; 3).
Xem lời giải »
Câu 4:
Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có D(3; 4), E(6; 1), F(7; 3) lần lượt là trung điểm của các cạnh AB, BC, CA. Tổng tung độ ba đỉnh của tam giác ABC là:
A. \(\frac{{16}}{3}\);
B. \(\frac{8}{3}\);
C. 8;
D. 16.
Xem lời giải »
Câu 5:
Trong mặt phẳng tọa độ Oxy, cho ba điểm A(0; – 1), B(1; 4), C(– 6; 5) không thẳng hàng. Tọa độ điểm D thỏa mãn ACBD là hình thang có AC // BD và AC = 2BD là:
A. D(7; –1);
B. D(4; 1);
C. D(–2; 7);
D. D(– 4; –1).
Xem lời giải »



