15 Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác (có đáp án) - Cánh diều Trắc nghiệm Toán 10
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
15 Bài tập Giá trị lượng giác của một góc từ 0 độ đến 180 độ. Định lý côsin và định lý sin trong tam giác (có đáp án) - Cánh diều Trắc nghiệm Toán 10
Câu 1. Tam giác ABC có A B = 5 , B C = 7 , C A = 8 A ^
A. 30 ° ;
B. 45 ° ;
C. 60 ° ;
D. 90 ° .
Hiển thị đáp án
Đáp án đúng là: C
Theo định lí hàm cosin, ta có: cos A ^ = A B 2 + A C 2 − B C 2 2 A B . A C = 5 2 + 8 2 − 7 2 2.5.8 = 1 2
Do đó, A ^ = 60 °
Câu 2. Tam giác ABC có A B = 2 , A C = 1 A ^ = 60 °
A. BC = 1;
B. BC = 2;
C. BC = 2 ;
D. BC = 3
Hiển thị đáp án
Đáp án đúng là: D
Theo định lí hàm cosin, ta có:
B C 2 = A B 2 + A C 2 − 2 A B . A C . cos A ^ = 2 2 + 1 2 − 2.2.1. cos 60 ° = 3 ⇒ B C = 3
Câu 3. Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh
AB = 9 và A C B ^ = 60 °
A. B C = 3 + 3 6 ;
B. B C = 3 6 − 3 ;
C. B C = 3 7 ;
D. B C = 3 + 3 33 2 .
Hiển thị đáp án
Đáp án đúng là: A
Gọi M, N lần lượt là trung điểm của AB, BC.
⇒ Δ A B C
⇒ M N = 1 2 A C
Theo định lí hàm cosin, ta có:
A B 2 = A C 2 + B C 2 − 2. A C . B C . cos A C B ^
⇔ 9 2 = 6 2 + B C 2 − 2.6. B C . cos 60 °
⇔ B C 2
⇔ 6
Câu 4. Tam giác ABC có A B = 2 , A C = 3 C ^ = 45 °
A. B C = 5 ;
B. B C = 6 + 2 2 ;
C. B C = 6 − 2 2 ;
D. B C = 6 .
Hiển thị đáp án
Đáp án đúng là: B
Theo định lí hàm cosin, ta có:
A B 2 = A C 2 + B C 2 − 2. A C . B C . cos C ^
⇒ 2 2 = 3 2 + B C 2 − 2. 3 . B C . cos 45 °
⇒ B C 2 6
⇒ B C = 6 + 2 2
Câu 5. Tam giác ABC có B ^ = 60 ° , C ^ = 45 °
A. A C = 5 6 2 ;
B. A C = 5 3 ;
C. A C = 5 2 ;
D. AC = 10
Hiển thị đáp án
Đáp án đúng là: A
Theo định lí hàm sin, ta có:
A B sin C ^ = A C sin B ^ ⇔ 5 sin 45 ° = A C sin 60 ° ⇒ A C = 5 6 2 .
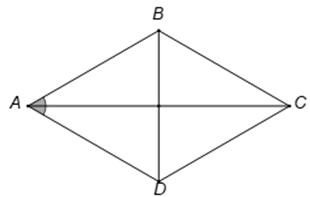
Câu 6. Cho hình thoi ABCD cạnh bằng 1cm và có B A D ^ = 60 °
A. A C = 3 ;
B. A C = 2 ;
C. A C = 2 3 ;
D. AC = 2.
Hiển thị đáp án
Đáp án đúng là: A
Do ABCD là hình thoi, có B A D ^ = 60 ° ⇒ A B C ^ = 120 °
Theo định lí hàm cosin, ta có:
A C 2 = A B 2 + B C 2 − 2. A B . B C . cos A B C ^
⇒ 1 2 + 1 2 − 2.1.1. cos 120 ° = 3 ⇒ A C = 3
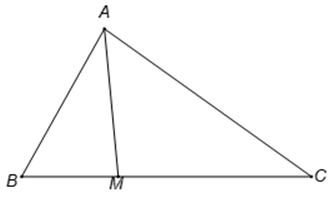
Câu 7. Tam giác ABC có A B = 4 , B C = 6 , A C = 2 7
A. A M = 4 2 ;
B. A M = 3 ;
C. A M = 2 3 ;
D. A M = 3 2 .
Hiển thị đáp án
Đáp án đúng là: C
Theo định lí hàm cosin, ta có : cos B = A B 2 + B C 2 − A C 2 2. A B . B C = 4 2 + 6 2 − 2 7 2 2.4.6 = 1 2
Do M C = 2 M B ⇒ B M = 1 3 B C = 2
A M 2 = A B 2 + B M 2 − 2. A B . B M . cos B ^
⇒ 4 2 + 2 2 − 2.4.2. 1 2 = 12 ⇒ A M = 2 3
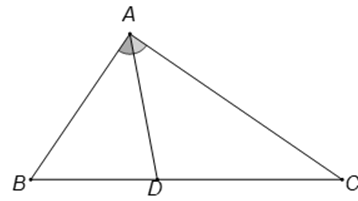
Câu 8. Tam giác ABC có A B = 6 − 2 2 , B C = 3 , C A = 2 A ^ A D B ^
A. 45 ° ;
B. 60 ° ;
C. 75 ° ;
D. 90 ° .
Hiển thị đáp án
Đáp án đúng là: C
Theo định lí hàm cosin, ta có:
cos B A C ^ = A B 2 + A C 2 − B C 2 2. A B . A C = − 1 2
⇒ B A C ^ = 120 ° ⇒ B A D ^ = 60 °
cos A B C ^ = A B 2 + B C 2 − A C 2 2. A B . B C = 2 2 ⇒ A B C ^ = 45 °
Trong Δ A B D B A D ^ = 60 ° , A B D ^ = 45 ° ⇒ A D B ^ = 75 °
Câu 9 . Tam giác ABC có A B = 3 , A C = 6 A ^ = 60 °
A. R = 3
B. R = 3 3
C. R = 3 ;
D. R = 6.
Hiển thị đáp án
Đáp án đúng là: A
Áp dụng định lí Cosin, ta có:B C 2 = A B 2 + A C 2 − 2 A B . A C . cos B A C ^
= 3 2 + 6 2 − 2.3.6. c o s 60 0 = 27 ⇔ B C 2 = 27 ⇔ B C 2 + A B 2 = A C 2 .
Suy ra tam giác ABC vuông tại B do đó bán kính R = A C 2 = 3.
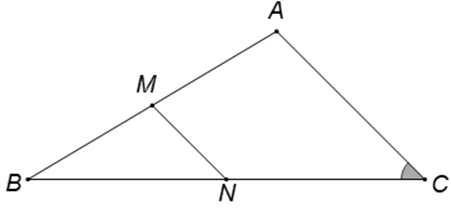
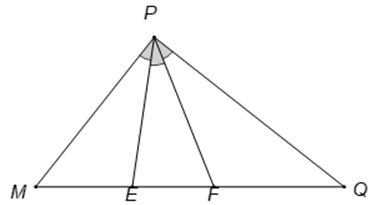
Câu 10. Tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E, F sao cho các góc M P E ^ , E P F ^ , F P Q ^ M P = q , P Q = m , P E = x , P F = y
A. M E = E F = F Q ;
B. M E 2 = q 2 + x 2 − x q ;
C. M F 2 = q 2 + y 2 − y q ;
D. M Q 2 = q 2 + m 2 − 2 q m .
Hiển thị đáp án
Đáp án đúng là: C
Ta có:M P E ^ = E P F ^ = F P Q ^ = M P Q ^ 3 = 30 ° ⇒ M P F ^ = E P Q ^ = 60 °
Theo định lí hàm cosin, ta có:
M E 2 = M P 2 + P E 2 − 2. M P . P E . cos M P E ^
⇒ q 2 + x 2 − 2 q x . cos 30 ° = q 2 + x 2 − q x 3
M F 2 = M P 2 + P F 2 − 2 M P . P F . cos M P F ^
⇒ q 2 + y 2 − 2 q y . cos 60 ° = q 2 + y 2 − q y
M Q 2 = M P 2 + P Q 2 = q 2 + m 2
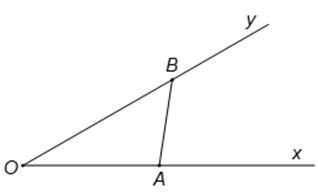
Câu 11. Cho góc x O y ^ = 30 °
A. 3 2 ;
B. 3 ;
C. 2 2 ;
D. 2.
Hiển thị đáp án
Đáp án đúng là: D
Theo định lí hàm sin, ta có:
O B sin O A B ^ = A B sin A O B ^ ⇔ O B = A B sin A O B ^ . sin O A B ^
⇔ 1 sin 30 ° . sin O A B ^ = 2 sin O A B ^
Do đó, độ dài OB lớn nhất khi và chỉ khi
sin O A B ^ = 1 ⇔ O A B ^ = 90 °
Khi đó OB = 2.
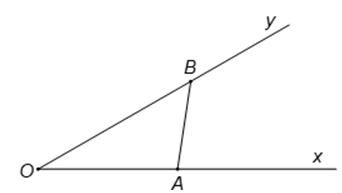
Câu 12. Cho góc x O y ^ = 30 °
sao cho AB = 1. Khi OB có độ dài lớn nhất thì độ dài của đoạn OA bằng:
A. 3 2 ;
B. 3 ;
C. 2 2 ;
D. 2.
Hiển thị đáp án
Đáp án đúng là: B
Theo định lí hàm sin, ta có:
O B sin O A B ^ = A B sin A O B ^ ⇔ O B = A B sin A O B ^ . sin O A B ^
⇔ 1 sin 30 ° . sin O A B ^ = 2 sin O A B ^
Do đó, độ dài OB lớn nhất khi và chỉ khi: <sin O A B ^ = 1 ⇔ O A B ^ = 90 °
Khi đó OB = 2.Tam giác OAB vuông tại A ⇒ O A = O B 2 − A B 2 = 2 2 − 1 2 = 3
Câu 13. Tam giác ABC có A B = c , B C = a , C A = b b b 2 − a 2 = c a 2 − c 2 B A C ^
A. 30 ° ;
B. 45 ° ;
C. 60 ° ;
D. 90 ° .
Hiển thị đáp án
Đáp án đúng là: C
Theo định lí hàm cosin, ta có: cos B A C ^ = A B 2 + A C 2 − B C 2 2. A B . A C = c 2 + b 2 − a 2 2 b c
Mà b b 2 − a 2 = c a 2 − c 2 ⇔ b 3 − a 2 b = a 2 c − c 3
⇔ − a 2 b + c + b 3 + c 3 = 0
⇔ b + c b 2 + c 2 − a 2 − b c = 0
⇔ b 2 + c 2 − a 2 − b c = 0 b > 0 , c > 0
⇔ b 2 + c 2 − a 2 = b c
Khi đó, cos B A C ^ = b 2 + c 2 − a 2 2 b c = 1 2 ⇒ B A C ^ = 60 °
Câu 14. Tam giác ABC vuông tại A, có A B = c , A C = b B A C ^
A. m = 2 b c b + c ;
B. m = 2 b + c b c ;
C. m = 2 b c b + c ;
D. m = 2 b + c b c .
Hiển thị đáp án
Đáp án đúng là: A
Ta có:B C = A B 2 + A C 2 = b 2 + c 2
Do AD là phân giác trong của B A C ^
⇒ B D = A B A C . D C = c b . D C = c b + c . B C = c b 2 + c 2 b + c
Theo định lí hàm cosin, ta có:
B D 2 = A B 2 + A D 2 − 2. A B . A D . cos A B D ^
⇔ c 2 b 2 + c 2 b + c 2 = c 2 + A D 2 − 2 c . A D . cos 45 °
⇒ A D 2 − c 2 . A D + c 2 − c 2 b 2 + c 2 b + c 2 = 0
⇔ A D 2 − c 2 . A D + 2 b c 3 b + c 2 = 0
⇒ A D = 2 b c b + c m = 2 b c b + c
Câu 15 . Tam giác ABC có BC = 10 và A ^ = 30 O
A. R = 5;
B. R = 10;
C. R = 10 3 ;
D. R = 10 3 .
Hiển thị đáp án
Đáp án đúng là: B
Áp dụng định lí sin, ta có: B C sin B A C ^ = 2 R ⇒ R = B C 2. sin A ^ = 10 2. sin 30 0 = 10.
Câu 1:
Tam giác ABC có A B = 5 , B C = 7 , C A = 8 A ^ bằng:
A. 30 ° ;
B. 45 ° ;
C. 60 ° ;
D. 90 ° ;
Xem lời giải »
Câu 2:
Tam giác ABC có A B = 2 , A C = 1 và A ^ = 60 ° . Tính độ dài cạnh BC.
A. BC = 1;
B. BC = 2;
C. BC = 2 ;
D. BC = 3
Xem lời giải »
Câu 3:
Tam giác ABC có đoạn thẳng nối trung điểm của AB và BC bằng 3, cạnh AB = 9 và A C B ^ = 60 ° . Tính độ dài cạnh cạnh BC.
A. B C = 3 + 3 6 ;
B. B C = 3 6 − 3 ;
C. B C = 3 7
D. B C = 3 + 3 33 2 .
Xem lời giải »
Câu 4:
Tam giác ABC có A B = 2 , A C = 3 và C ^ = 45 ° . Tính độ dài cạnh BC .
A. B C = 5 ;
B. B C = 6 + 2 2 ;
C. B C = 6 - 2 2 ;
D. B C = 6 ;
Xem lời giải »
Câu 5:
Tam giác ABC có B ^ = 60 ° , C ^ = 45 ° và AB = 5 . Tính độ dài cạnh AC .
A. A C = 5 6 2 ;
B. A C = 5 3 ;
C. A C = 5 2 ;
D. A C = 10.
Xem lời giải »
Câu 6:
Cho hình thoi ABCD cạnh bằng 1cm và có B A D ^ = 60 ° . Tính độ dài AC.
A. A C = 3 ;
B. A C = 2 ;
C. A C = 2 3 ;
D. A C = 2
Xem lời giải »
Câu 7:
Tam giác ABC có A B = 4 , B C = 6 , A C = 2 7 . Điểm M thuộc đoạn BC sao cho MC = 2MB . Tính độ dài cạnh AM. .
A. A M = 4 2 ;
B. A M = 3 ;
C. A M = 2 3 ;
D. A M = 3 2 ;
Xem lời giải »
Câu 8:
Tam giác ABC có A B = 6 − 2 2 , B C = 3 , C A = 2 . Gọi D là chân đường phân giác trong góc A ^ . Khi đó góc A D B ^ bằng bao nhiêu độ?
A. 45 ° ;
B. 60 ° ;
C. 75 ° ;
D. 90 ° ;
Xem lời giải »
Câu 9:
Tam giác ABC có A B = 3 , A C = 6 và A ^ = 60 ° . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC .
A. R = 3 ;
B. R = 3 3 ;
C. R = 3 ;
D. R = 6 ;
Xem lời giải »
Câu 10:
Tam giác MPQ vuông tại P. Trên cạnh MQ lấy hai điểm E, F sao cho các góc M P E ^ , E P F ^ , F P Q ^ bằng nhau. Đặt M P = q , P Q = m , P E = x , P F = y . Trong các hệ thức sau, hệ thức nào đúng?
A. M E = E F = F Q ;
B. M E 2 = q 2 + x 2 − x q ;
C. M F 2 = q 2 + y 2 − y q ;
D. M Q 2 = q 2 + m 2 − 2 q m .
Xem lời giải »
Câu 11:
Cho góc x O y ^ = 30 ° . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1 . Độ dài lớn nhất của đoạn OB bằng:
A. 3 2 ;
B. 3 ;
C. 2 2
D. 2
Xem lời giải »
Câu 12:
Cho góc x O y ^ = 30 ° . Gọi A và B là hai điểm di động lần lượt trên Ox và Oy sao cho AB = 1 . Khi OB có độ dài lớn nhất thì độ dài của đoạn OA bằng:
A. 3 2 ;
B. 3 ;
C. 2 2
D. 2
Xem lời giải »
Câu 13:
Tam giác ABC có A B = c , B C = a , C A = b . Các cạnh a, b, c liên hệ với nhau bởi đẳng thức b b 2 − a 2 = c a 2 − c 2 . Khi đó góc B A C ^ bằng bao nhiêu độ?
A. 30 ° ;
B. 45 ° ;
C. 60 ° ;
D. 90 ° ;
Xem lời giải »
Câu 14:
Tam giác ABC vuông tại A , có A B = c , A C = b . Gọi m là độ dài đoạn phân giác trong góc B A C ^ . Tính m theo b và c .
A. m = 2 b c b + c ;
B. m = 2 b + c b c ;
C. m = 2 b c b + c ;
D. m = 2 b + c b c .
Xem lời giải »
Câu 15:
Tam giác ABC có BC = 10 và A ^ = 30 O . Tính bán kính R của đường tròn ngoại tiếp tam giác ABC .
B. R = 10;
C. R = 10 3 ;
D. R = 10 3 .
Xem lời giải »
Câu 1:
Khẳng định nào sau đây là đúng?
A. sin157° = −sin23°;
B. sin157° = −cos23°;
C. sin157° = cos23°;
D. sin157° = sin23°.
Xem lời giải »
Câu 2:
Cho góc x thoả 0° < x < 90°. Mệnh đề nào sau đây là sai?
A. cos x < 0;
B. sin x > 0;
C. tan x > 0;
D. cot x > 0.
Xem lời giải »
Câu 3:
Cho góc α là góc tù. Khẳng định nào sau đây là đúng?
A. tan α < 0;
B. sin α < 0;
C. cot α > 0;
D. cos α > 0.
Xem lời giải »
Câu 4:
Giá trị của cos 30° + sin 60° bằng bao nhiêu?
B. 3 2
C. 3
D. 1.
Xem lời giải »
Câu 5:
Cho α và β là hai góc khác nhau và bù nhau, trong các đẳng thức sau đây đẳng thức nào sai?
A. sin α = sin β;
B. cos α = – cos β;
C. tan α = – tan β;
D. cot α = cot β.
Xem lời giải »
Câu 6:
Biết cos α = - 5 13
A. − 12 13 ; 2 3
B. 2 3 ; − 5 12
C. − 12 13 ; 12 5
D. 12 13 ; − 12 5
Xem lời giải »
Câu 7:
Giá trị của biểu thức P = asin0° + bcos0° + csin90° bằng:
A. a – b;
B. b + c;
C. a – c;
D. a + c.
Xem lời giải »
Câu 1:
Giá trị của biểu thức S = 2 + sin2 90° + 2cos2 60° − 3tan2 45° bằng:
A. 1 2
B. - 1 2
C. 1;
D. 3.
Xem lời giải »
Câu 2:
Cho biểu thức P = 3sin2 x + 5cos2 x, biết cos x = 1 2 . Giá trị của P bằng:
B. 7 2
C. 7;
D. 13 4
Xem lời giải »
Câu 3:
Tam giác ABC có AB = 5, BC = 7, CA = 8. Số đo góc A bằng:
A. 60°;
B. 30°;
C. 45°;
D. 90°.
Xem lời giải »
Câu 4:
Tam giác ABC có B ^ C ^
B. AC = 7 6 2
C. AC = 7 2
D. AC = 10.
Xem lời giải »
Câu 5:
Nếu sin x + cos x = 1 2
A. 5 − 7 4 h a y 5 + 7 4
B. 5 − 5 7 h a y 5 + 5 7
C. 2 − 3 5 h a y 2 + 3 5
D. 3 − 2 5 h a y 3 + 2 5
Xem lời giải »
Câu 6:
Trong tam giác MNP với NP = a, MP = b, ta có:
A. a.sinM = b.sinN;
B. a.sinN = b.sinM;
C. a.cosN = b.cosM;
D. a.cosM = b.cosN.
Xem lời giải »
Câu 7:
Cho tam giác ABC có BC = 12 và A ^
A. R = 12 3
B. R = 12;
C. R = 12 3
D. R = 4 3
Xem lời giải »
Câu 8:
Cho tan α + cot α = m với 0° < α < 90°. Tìm m để tan2 α + cot2 α = 7.
A. m = 9;
B. m = 3;
C. m = – 3;
D. m = ± 3.
Xem lời giải »
Câu 1:
Biểu thức P = cos2 x.cot2 x + 4cos2 x – cot2 x + 3sin2 x có giá trị là
A. 2;
B. −2;
C. 3;
D. −3.
Xem lời giải »
Câu 2:
Biết tan x = 2 b a − c . Giá trị của biểu thức A = a.cos2 x + 2b.sin x.cos x + c.sin2 x bằng
A. a;
B. −a;
C. b;
D. c.
Xem lời giải »
Câu 3:
Cho cot α = −2. Khi đó 3 sin α − 2 cos α 12 sin 3 α + 4 cos 3 α
B. - 7 4
C. 3 4
D. 1 4
Xem lời giải »
Câu 4:
Kết quả đơn giản của biểu thức sin α + tan α cos α + 1 2 + 1
A. 1 cos 2 α
B. 1 + tan α;
C. 2;
D. 1 sin 2 α
Xem lời giải »
Câu 5:
Hai chiếc tàu thuỷ cùng xuất phát từ vị trí A, đi thẳng theo hai hướng tạo với nhau một góc 60°. Tàu thứ nhất chạy với tốc độ 30 km/h, tàu thứ hai chạy với tốc độ 40 km/h. Hỏi sau 2 giờ hai tàu cách nhau bao nhiêu km?
B. 15 13
C. 20 13
D. 15.
Xem lời giải »