15 Bài tập Bất phương trình bậc hai một ẩn (có đáp án) - Cánh diều Trắc nghiệm Toán 10
Haylamdo biên soạn và sưu tầm với 15 bài tập trắc nghiệm Bất phương trình bậc hai một ẩn Toán lớp 10 có đáp án và lời giải chi tiết đầy đủ các mức độ sách Cánh diều sẽ giúp học sinh ôn luyện trắc nghiệm để biết cách làm các dạng bài tập Toán 10.
15 Bài tập Bất phương trình bậc hai một ẩn (có đáp án) - Cánh diều Trắc nghiệm Toán 10
Câu 1. Tập nghiệm của bất phương trình: 2 x 2 – 7 x – 15 ≥ 0
Hiển thị đáp án
Đáp án đúng là : A
Ta có : f(x) = 2 x 2 – 7 x – 15 = 0 ⇔
Bảng xét dấu
Dựa vào bảng xét dấu 2 x 2 – 7 x – 15 ≥ 0 ⇔
Câu 2. Tập nghiệm của bất phương trình: – x 2 + 6 x + 7 ≥ 0
Hiển thị đáp án
Đáp án đúng là : B
Ta có : f(x) = – x 2 + 6 x + 7 = 0 ⇔
Bảng xét dấu
Dựa vào bảng xét dấu – x 2 + 6 x + 7 ≥ 0 ⇔ − 1 ≤ x ≤ 7.
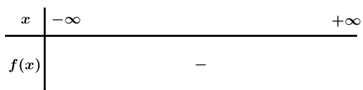
Câu 3. Giải bất phương trình − 2 x 2 + 3 x − 7 ≥ 0.
A. S = 0 ;
B. S = 0 ;
C. S = ∅ ;
D. S = ℝ .
Hiển thị đáp án
Đáp án đúng là: C
Ta có : f(x) = – 2 x 2 + 3 x − 7 = 0
Bảng xét dấu
Dựa vào bảng xét dấu : − 2 x 2 + 3 x − 7 ≥ 0 ⇔ x ∈ ∅
Câu 4 . Tập nghiệm của bất phương trình x 2 − 3 x + 2 < 0
A. − ∞ ; 1 ∪ 2 ; + ∞ ;
B. 2 ; + ∞ ;
C. 1 ; 2 ;
D. − ∞ ; 1 .
Hiển thị đáp án
Đáp án đúng là: C
Ta có : f x = x 2 − 3 x + 2 = 0 ⇔
Bảng xét dấu
Dựa vào bảng xét dấu f x < 0 ⇔ 1 < x < 2
Câu 5 . Tập nghiệm của bất phương trình − x 2 + 5 x − 4 < 0
A.
B.1 ; 4
C. − ∞ ; 1 ∪ 4 ; + ∞
D. − ∞ ; 1 ∪ 4 ; + ∞ .
Hiển thị đáp án
Đáp án đúng là: C
Ta có: f x = − x 2 + 5 x − 4 = 0 ⇔
Bảng xét dấu
Dựa vào bảng xét dấu f x < 0 ⇔
Câu 6 . Tập nghiệm của bất phương trình 2 x 2 − 2 + 1 x + 1 < 0
A. 2 2 ; 1 ;
B. ∅ ;
C.
D. − ∞ ; 2 2 ∪ 1 ; + ∞ .
Hiển thị đáp án
Đáp án đúng là: A
Ta có: f x = 2 x 2 − 2 + 1 x + 1 = 0 ⇔
Bảng xét dấu
Dựa vào bảng xét dấu f x < 0 ⇔ 2 2 < x < 1
Câu 7 . Tập nghiệm của bất phương trình 6 x 2 + x − 1 ≤ 0
Hiển thị đáp án
Đáp án đúng là : A
Ta có: f x = 6 x 2 + x − 1 = 0 ⇔
Bảng xét dấu
Dựa vào bảng xét dấu f x ≤ 0 ⇔ − 1 2 ≤ x ≤ 1 3
Câu 8 . Số thực dương lớn nhất thỏa mãn x 2 − x − 12 ≤ 0
A. 1
B. 2
C. 3
D. 4
Hiển thị đáp án
Đáp án đúng là :D
Ta có f x = x 2 − x − 12 = 0 ⇔
Bảng xét dấu
Dựa vào bảng xét dấu f x ≤ 0 ⇔ − 3 ≤ x ≤ 4 x 2 − x − 12 ≤ 0
Câu 9 . Bất phương trình nào sau đây có tập nghiệm là ℝ
A. − 3 x 2 + x − 1 ≥ 0 ;
B. − 3 x 2 + x − 1 > 0 ;
C. − 3 x 2 + x − 1 < 0 ;
D. − 3 x 2 + x − 1 ≤ 0.
Hiển thị đáp án
Đáp án đúng là: C
- Xét f x = − 3 x 2 + x − 1 a = − 3 < 0 , Δ = 1 2 − 4. − 3 . − 1 = − 11 < 0 f x < 0 , ∀ x ℝ
Như vậy chỉ có đáp án C là phù hợp, các đáp án còn lại đều vô nghiệm.
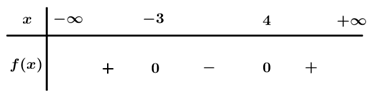
Câu 10 . Cho bất phương trình x 2 − 8 x + 7 ≥ 0 không phải là nghiệm của bất phương trình.
Hiển thị đáp án
Đáp án đúng là: D
Ta có: f x = x 2 − 8 x + 7 = 0 ⇔
Bảng xét dấu
Dựa vào bảng xét dấu f x ≥ 0 ⇔
Tập nghiệm của bất phương trình là S = − ∞ ; 1 ∪ 7 ; + ∞
Vì 13 2 ∈ 6 ; + ∞ 13 2 ∉ S 6 ; + ∞
Câu 11 . Giải bất phương trình x x + 5 ≤ 2 x 2 + 2 .
A. x ≤ 1 ;
B. 1 ≤ x ≤ 4 ;
C.
D. x ≥ 4.
Hiển thị đáp án
Đáp án đúng là: C
Bất phương trình x x + 5 ≤ 2 x 2 + 2 ⇔ x 2 + 5 x ≤ 2 x 2 + 4 ⇔ x 2 − 5 x + 4 ≥ 0
Xét phương trình x 2 − 5 x + 4 = 0 ⇔ x − 1 x − 4 = 0 ⇔
Lập bảng xét dấu
Dựa vào bảng xét dấu, ta thấy x 2 − 5 x + 4 ≥ 0
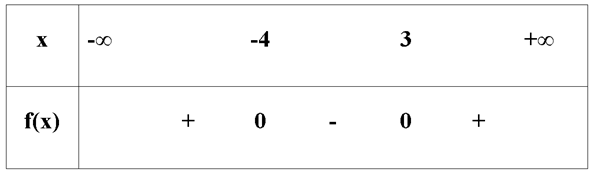
Câu 12 . Tập nghiệm S của bất phương trình x 2
A. S = − 4 ; 3 ;
B. S = 4 ; + ∞ ;
C. S = 3 ; + ∞ ;
D. S = ∅ .
Hiển thị đáp án
Đáp án đúng là: A
Tam thức bậc hai f(x) = x 2
f(x) < 0 suy ra -4 < x < 3.
Câu 13 . Tổng các nghiệm nguyên của bất phương trình x 2 − x ≥ x 7 − x − 6 x − 1
A. 5;
B. 6;
C. 21;
D. 40;
Hiển thị đáp án
Đáp án đúng là: D
Bất phương trình:
x 2 − x ≥ x 7 − x − 6 x − 1 ⇔ 2 x − x 2 ≥ 7 x − x 2 − 6 x + 6 ⇔ x ≥ 6 x ∈ 6 ; 7 ; 8 ; 9 ; 10
Tổng các nghiệm nguyên là 6 + 7 + 8 + 9 + 10 = 40.
Câu 14. Bất phương trình2 x − 1 x + 3 − 3 x + 1 ≤ x − 1 x + 3 + x 2 − 5
A. S = − ∞ ; − 2 3 ;
B.
C. S = ℝ ;
D. S = ∅ .
Hiển thị đáp án
Đáp án đúng là: D
Bất phương trình 2 x − 1 x + 3 − 3 x + 1 ≤ x − 1 x + 3 + x 2 − 5 2 x 2 + 5 x − 3 − 3 x + 1 ≤ x 2 + 2 x − 3 + x 2 − 5
0. x ≤ − 6 ⇔ x ∈ ∅ Do đó tập nghiệm S = ∅
Câu 15. Tập nghiệm S của bất phương trình5 x + 1 − x 7 − x > − 2 x
A. S = ℝ ;
B. S = − 5 2 ; + ∞ ;
C. S = − ∞ ; 5 2 ;
D. S = ∅ .
Hiển thị đáp án
Đáp án đúng là: A
Bất phương trình 5 x + 1 − x 7 − x > − 2 x
5 x + 5 − 7 x + x 2 > − 2 x ⇔ x 2 + 5 > 0 x 2 x ∈ ℝ x 2 + 5 > 0 x ∈ ℝ S = ℝ ;
Câu 1:
Tập nghiệm của bất phương trình: 2 x 2 – 7 x – 15 ≥ 0 là:
A. – ∞ ; – 3 2 ∪ 5 ; + ∞ ;
B. – 3 2 ; 5
C. − ∞ ; − 5 ∪ 3 2 ; + ∞
D. - 5 ; 3 2
Xem lời giải »
Câu 2:
Tập nghiệm của bất phương trình: – x 2 + 6 x + 7 ≥ 0 là:
A. − ∞ ; − 1 ∪ 7 ; + ∞
B. − 1 ; 7
C. − ∞ ; − 7 ∪ 1 ; + ∞
D. − 7 ; 1
Xem lời giải »
Câu 3:
Giải bất phương trình − 2 x 2 + 3 x − 7 ≥ 0.
B. S = 0
B. S = 0 ;
C. S = ∅ ;
D. S = ℝ
Xem lời giải »
Câu 4:
Tập nghiệm của bất phương trình x 2 − 3 x + 2 < 0 là:
A. − ∞ ; 1 ∪ 2 ; + ∞ ;
B. 2 ; + ∞ ;
C. 1 ; 2 ;
D. − ∞ ; 1 .
Xem lời giải »
Câu 5:
Tập nghiệm của bất phương trình − x 2 + 5 x − 4 < 0 là :
A. 1 ; 4
B. 1 ; 4
C. − ∞ ; 1 ∪ 4 ; + ∞
D. − ∞ ; 1 ∪ 4 ; + ∞
Xem lời giải »
Câu 6:
Tập nghiệm của bất phương trình 2 x 2 − 2 + 1 x + 1 < 0 là:
A. 2 2 ; 1 ;
B. ∅ ;
C. 2 2 ; 1 ;
D. − ∞ ; 2 2 ∪ 1 ; + ∞ .
Xem lời giải »
Câu 7:
Tập nghiệm của bất phương trình 6 x 2 + x − 1 ≤ 0 là
A. − 1 2 ; 1 3
B. − 1 2 ; 1 3
C. − ∞ ; − 1 2 ∪ 1 3 ; + ∞
D. − ∞ ; − 1 2 ∪ 1 3 ; + ∞
Xem lời giải »
Câu 8:
Số thực dương lớn nhất thỏa mãn x 2 − x − 12 ≤ 0 là ?
A. 1
B. 2
C. 3
D. 4
Xem lời giải »
Câu 9:
Bất phương trình nào sau đây có tập nghiệm là ℝ
A. − 3 x 2 + x − 1 ≥ 0 ;
B. − 3 x 2 + x − 1 > 0 ;
C. − 3 x 2 + x − 1 < 0 ;
D. − 3 x 2 + x − 1 ≤ 0.
Xem lời giải »
Câu 10:
Cho bất phương trình x 2 − 8 x + 7 ≥ 0 không phải là nghiệm của bất phương trình.
A. − ∞ ; 0 ;
B. 8 ; + ∞ ;
C. − ∞ ; 1 ;
D. 6 ; + ∞ .
Xem lời giải »
Câu 11:
Giải bất phương trình x x + 5 ≤ 2 x 2 + 2 .
A. x ≤ 1 ;
B. 1 ≤ x ≤ 4 ;
C. x ∈ − ∞ ; 1 ∪ 4 ; + ∞ ;
D. x ≥ 4.
Xem lời giải »
Câu 12:
Tập nghiệm S của bất phương trình x 2 + x - 12 < 0 là:
A. S = − 4 ; 3 ;
B. S = 4 ; + ∞ ;
C. S = 3 ; + ∞ ;
D. S = ∅ .
Xem lời giải »
Câu 13:
Tổng các nghiệm nguyên của bất phương trình x 2 − x ≥ x 7 − x − 6 x − 1 trên đoạn − 10 ; 10 bằng:
A. 5
B. 6
C. 21
D. 40
Xem lời giải »
Câu 14:
B ất phương trình 2 x − 1 x + 3 − 3 x + 1 ≤ x − 1 x + 3 + x 2 − 5 có tập nghiệm là:
A. S = − ∞ ; − 2 3 ;
B. S = − 2 3 ; + ∞ ;
C. S = ℝ
D. S = ∅ .
Xem lời giải »
Câu 15:
Tập nghiệm S của bất phương trình 5 x + 1 − x 7 − x > − 2 x là:
A. S = ℝ ;
B. S = − 5 2 ; + ∞ ;
C. S = − ∞ ; 5 2 ;
D. S = ∅ .
Xem lời giải »
Câu 1:
Bất phương trình nào sau đây là bất phương trình bậc hai một ẩn?
A. 2x2 – 8x + 12 ≥ 0;
B. 1 x + 1
C. 6x + 5 7
D. 2(x – 4) ≥3 x − 14 2
Xem lời giải »
Câu 2:
Cho bất phương trình bậc hai một ẩn x2 + 4x − 5 < 0 (1). Giá trị nào sau đây của x là nghiệm của bất phương trình?
A. x = 2;
B. x = 1;
C. x = 3;
D. x = −1.
Xem lời giải »
Câu 3:
Bất phương trình nào sau đây là bất phương trình bậc hai một ẩn?
A. x + 3 > 0;
B. 6x3 + 2 > 0;
C. 3x2 – 1 < 0;
D. 1 3
Xem lời giải »
Câu 4:
Dựa vào đồ thị hàm số bậc hai y = f(x) trong hình dưới đây. Tập nghiệm nào sau đây là tập nghiệm của bất phương trình f(x) > 0?
A. S = (−∞ ∪ ∞
B. S = (1; 4);
C. S = [1; 4];
D. S = (−∞ ∪ ∞
Xem lời giải »
Câu 5:
Dựa vào đồ thị hàm số bậc hai y = f(x) trong hình dưới đây. Tập nghiệm nào sau đây là tập nghiệm của bất phương trình f(x) ≤ 0?
B. S = ∅
C. S = ℝ;
D. S = {2}.
Xem lời giải »
Câu 6:
Tìm tập xác định của hàm số y =2 x + 5 1 − 2 x
B. D = − 5 2 ; + ∞
C. D = 1 2 ; + ∞
D. D = − ∞ ; 1 2
Xem lời giải »
Câu 7:
Dựa vào đồ thị hàm số bậc hai y = f(x) trong hình dưới đây. Tập nghiệm nào sau đây là tập nghiệm của bất phương trình f(x) ≥ 0?
A. S = ℝ\{1};
B. S = ∅
C. S = ℝ;
D. S = {1}.
Xem lời giải »
Câu 1:
Tập nghiệm của bất phương trình – x2 + 6x + 7 > 0.
A. S = (− 1; 7);
B. S = [− 7; 1];
C. S = (−3; 1];
D. S = (− ∞; −1) ∪
Xem lời giải »
Câu 2:
Tập nghiệm của bất phương trình (x2 – 3x + 1)2 + 3x2 – 9x + 5 > 0 là
A. S = (−∞
B. S = (2; +∞
C. S = (−∞ ∪ ∞
D. S = (0; 1).
Xem lời giải »
Câu 3:
Tìm tập nghiệm của bất phương trình 1 x 2 − 5 x + 4 1 x 2 − 7 x + 10
A. S = (1; 2);
B. S = (3; 4);
C. S = (5; +∞
D. S = (1; 2) ∪ ∪ ∞
Xem lời giải »
Câu 4:
Tìm các giá trị của a sao cho với mọi x, ta luôn có: −1 ≤ x 2 + 5 x + a 2 x 2 − 3 x + 2
A. - 5 3
B. a ≥ - 5 3
C. a < 1;
D. a ≤ 1.
Xem lời giải »
Câu 5:
Tìm m để bất phương trình (m – 1)x2 – 2(m + 1)x + 3(m – 2) > 0 có nghiệm đúng với mọi x ∈ ℝ.
A. m > 1;
B. m < 1;
C. m > 5;
D. m > 1 hay m > 5.
Xem lời giải »
Câu 6:
Tập nghiệm của bất phương trình 2x2 + x + 2 > 0 là:
A. ℝ;
B. ℝ \ {1};
C. ℝ \ {2};
D. ℝ \ {3}.
Xem lời giải »
Câu 7:
Tìm tập xác định của hàm số y = x 2 + 5 x + 4 2 x 2 + 3 x + 1
A. D = (−∞
B. D = − 1 2 ; + ∞
C. D = (−∞ ∪ − 1 2 ; + ∞
D. D = − 4 ; − 1 2
Xem lời giải »
Câu 8:
Tìm tất cả các giá trị thực của tham số m để bất phương trình sau vô nghiệm f(x) = (m – 3)x2 + (m + 2)x – 4 > 0.
A. m ≤ −22 hay m ≥ 2;
B. −22 ≤ m ≤ 2;
C. −22 < m < 2;
D. − 22 ≤ m ≤ 2 m = 3
Xem lời giải »
Câu 1:
Tập nghiệm của bất phương trình x − 1 2 x + 3 ( x + 1 ) ( x − 2 ) ( x − 3 ) > 0
A. S = (−∞ ∪ ∪ ∞
B. S = (−∞ ∪ ∪ ∞
C. S = (−∞ ∪ ∪ ∞
D. S = (−∞ ∪ ∪ ∞
Xem lời giải »
Câu 2:
Phương trình (m + 2) x2 – 3x + 2m – 3 = 0 có hai nghiệm trái dấu khi và chỉ khi
A. m < –2 hoặc m > 3 2
B. m > 3 2
C. − 2 < m < 3 2
D. m < 2.
Xem lời giải »
Câu 3:
Tìm m để bất phương trình sau (m + 2)2 – 2mx + m2 + 2m ≤ 0 có nghiệm.
A. m < 2;
B. |m| < 2;
C. m <2
D. |m| <2
Xem lời giải »
Câu 4:
Tìm tham số m để bất phương trình: f(x) = (m2 + 1)x2 + (2m – 1)x – 5 < 0 có nghiệm đúng với mọi x thuộc khoảng (−1; 1).
A. m ∈ − 1 ; 6
B. m ∈ 1 ; 6
C. m ∈ − 1 ; 6 − 1
D. m ∈ 1 ; 6 − 1
Xem lời giải »
Câu 5:
Bất phương trình mx2 – (2m – 1)x + m + 1 < 0 vô nghiệm khi và chỉ khi
A. m ≤ 1 8
B. m > 1 8
C. m < 1 8
D. m ≥ 1 8
Xem lời giải »
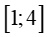
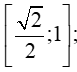
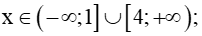
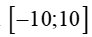

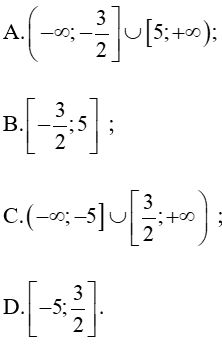
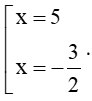
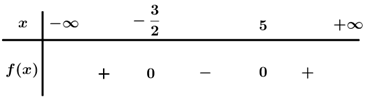
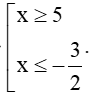
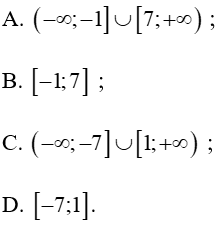
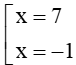 .
. 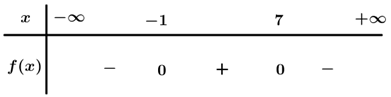
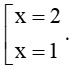
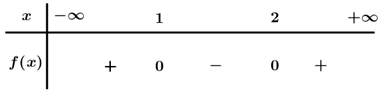
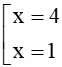 .
. 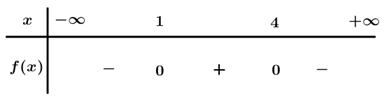
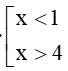 .
. 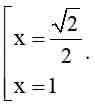
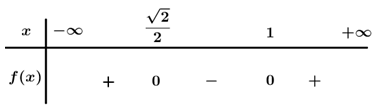
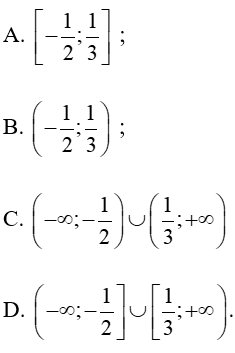
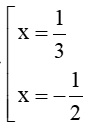 .
. 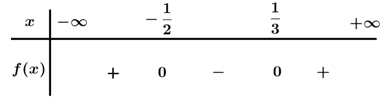
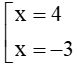 .
. 
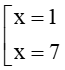 .
. 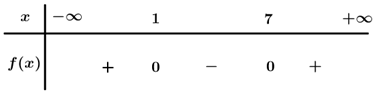
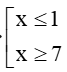 .
. 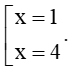
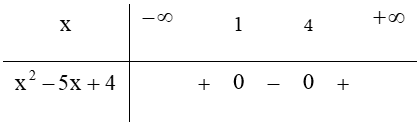
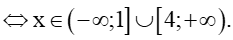
 và x nguyên nên ta có:.
và x nguyên nên ta có:.