Bài tập trắc nghiệm Áp dụng định lí Vi-ét - Toán lớp 9

Bài tập trắc nghiệm Áp dụng định lí Vi-ét

Với Bài tập trắc nghiệm Áp dụng định lí Vi-ét Toán lớp 9 tổng hợp 10 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Áp dụng định lí Vi-ét từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Câu 1: Tích hai nghiệm của phương trình -x² + 7x + 8 = 0 có giá trị bằng bao nhiêu?

A.8    B.-8    C.7    D.-7

Câu 2: Gọi P là tích 2 nghiệm của phương trình x² - 5x - 16 = 0 . Khi đó P bằng:

A. -5    B. 5    C. 16    D. -16

Câu 3: Phương trình x⁴ + 2² - 3 = 0 có tổng các nghiệm bằng:

A. -2    B. -1    C. 0    D. -3

Câu 4: Phương trình -3x² + 4x + 2 = 0 có tích hai nghiệm bằng:

A. 4/3    B. -6    C. -3/2    D. -2/3

Câu 5: Gọi S và P lần lươt là tổng và tích hai nghiệm của phương trình x² + 5x - 10 = 0. Khi đó S+P bằng:

A. -15    B. -10    C. -5    D. 5

Câu 6: Tích hai nghiệm của phương trình -x² + 5x + 6 là:

A. 6    B. -6    C. 5    D. -5

Câu 7: Phương trình x² - 3x - 5 có tổng hai nghiệm là:

A.3    B.-3    C. 5    D. -5

Câu 8: Cho phương trình x² - 4x + 1 = 0 . Với giá trị nào của m thì phương trình thỏa mãn hệ thức 5(x₁ + x₂) - 4x₁x₂ = 0

A. m= 4

B. m= -5

C. m= -4

D. Không có giá trị nào

Câu 9: Giả sử x₁, x₂ là 2 nghiệm của phương trình 2x² + 3x - 5 = 0 . Biểu thức x₁² + x₂² có giá trị là:

A.29/2 B.29 C. 29/4 D.25/4

Câu 10: Với giá trị nào của m thì phương trình x² - 2x + 3m - 1 = 0 có nghiệm x₁; x₂ thỏa mãn x₁² + x₂² = 10 ?

A. m = -4/3    B. m = 4/3    C. m = -2/3    D. m = 2/3

Hướng dẫn giải và đáp án

Câu 1: B

Câu 2: D

Câu 3: Đặt t= x² (t ≥ 0), khi đó ta có phương trình: t² + 2t - 3 = 0

⇔ t = 1(t/m) hoặc t = -3

Với t=1, ta có: x² = 1 => x= ±1. Từ đó suy ra tổng 2 nghiệm là 0

Vậy chọn đáp án: C

Câu 4: D

Câu 5: A

Câu 6: B

Câu 7: A

Câu 8: Phương trình có nghiệm ⇔ Δ' ≥ 0

⇔ 4 - (1-m) ≥ 0 ⇔ 3 + m ≥ 0 ⇔ m ≥ -3

Theo Vi-ét ta có:

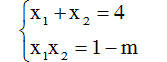
Thay vào 5(x₁ + x₂) - 4x₁x₂ ta được: 5.4 - 4 (1-m) = 0

⇔ 16 + 4m = 0 ⇔ m = -4 (loại)

Vậy chọn đáp án:D

Câu 9: Theo Vi-ét ta có:

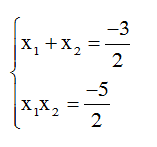
Ta có: x₁² + x₂² = (x₁ + x₂)² - 2x₁x₂ = 9/4 + 5 = 29/4

Vậy chọn đáp án C

Câu 10: Phương trình có nghiệm khi ⇔ Δ' ≥ 0

⇔ 2 - 3m ≥ 0

⇔ m ≤ 2/3

Theo vi ét ta có:

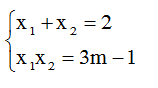
Ta có: x₁² + x₂² = 10

⇔ (x₁ + x₂)² - 2x₁.x₂ = 10

⇔ 4 - 2(3m - 1) = 10 ⇔ m = -2/3 (thỏa mãn)

Vậy chọn đáp án C