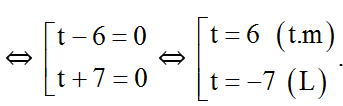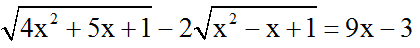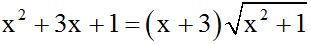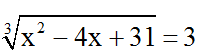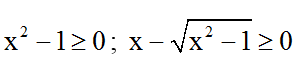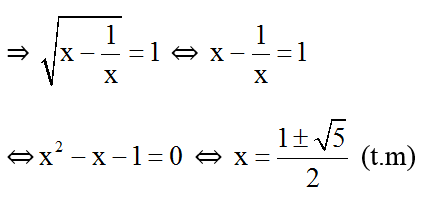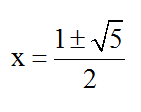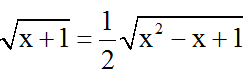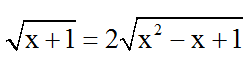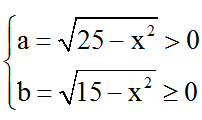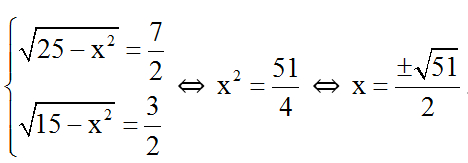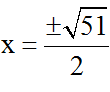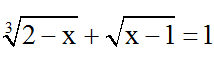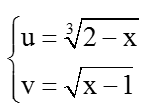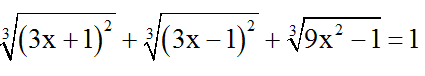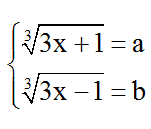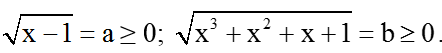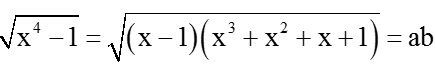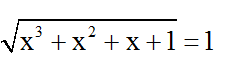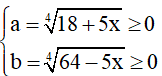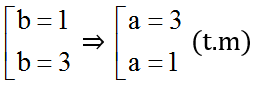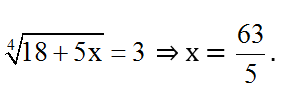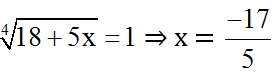Cách giải phương trình vô tỉ bằng phương pháp đặt ẩn phụ cực hay - Toán lớp 9

---

Cách giải phương trình vô tỉ bằng phương pháp đặt ẩn phụ cực hay

Với Cách giải phương trình vô tỉ bằng phương pháp đặt ẩn phụ cực hay Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập giải phương trình vô tỉ bằng phương pháp đặt ẩn phụ từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Phương pháp giải

Bước 1: Tìm đkxđ.

Bước 2: Đặt một (hoặc nhiều) biểu thức thích hợp làm ẩn mới, (thường là các biểu thức chứa căn thức) tìm điều kiện của ẩn mới.

Bước 3: Biến đổi phương trình theo ẩn mới (Có thể biến đổi hoàn toàn thành ẩn mới hoặc để cả 2 ẩn cũ và mới) rồi giải phương trình theo ẩn mới.

Bước 4: Thay trả lại ẩn cũ và tìm nghiệm, đối chiếu đkxđ và kết luận.

Ví dụ minh họa

Ví dụ 1: Giải phương trình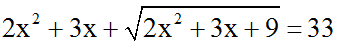

Hướng dẫn giải:

Đkxđ: ∀ x ∈ R.

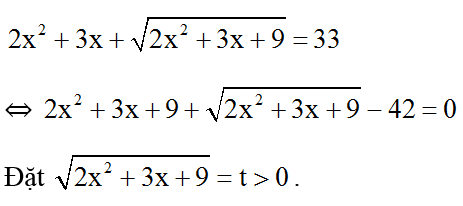
Phương trình trở thành:

t² + t – 42 = 0 ⇔ (t – 6)(t + 7) = 0

Với t = 6 ⇒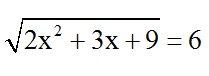

⇔ 2x² + 3x + 9 = 36

⇔ 2x² + 3x - 27 = 0

⇔ (x-3) (2x+9) = 0 .

⇔ x = 3 hoặc x = -9/2

Vậy phương trình có hai nghiệm x = 3 và x = -9/2.

Ví dụ 2: Giải phương trình

Hướng dẫn giải:

Đkxđ : 4x² + 5x + 1 ≥ 0

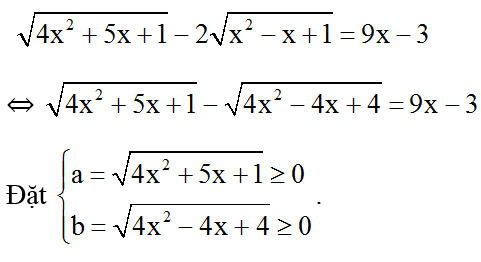
Phương trình trở thành : a - b = a² - b²

⇔ (a-b)(a+b-1) = 0 ⇔ a - b = 0 hoặc a + b - 1 = 0.

TH1 : a – b = 0 ⇔ 9x – 3 = 0 ⇔ x = 1/3 (t.m đkxđ).

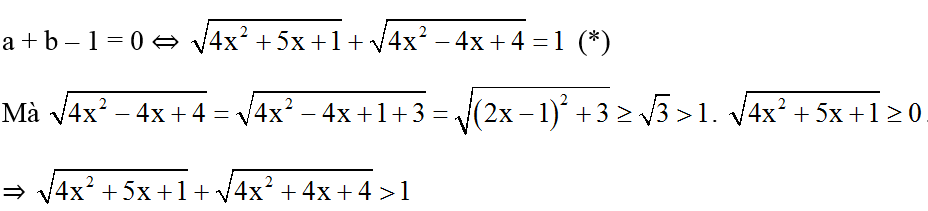
⇒ Phương trình (*) vô nghiệm.

Vậy phương trình có nghiệm duy nhất x = 1/3 .

Ví dụ 3: Giải phương trình:

Hướng dẫn giải:

Đkxđ: ∀ x ∈ R.

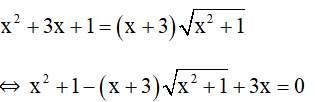
Phương trình trở thành: t² - (x+3)t + 3x = 0

⇔ (t-3)(t-x) = 0 ⇔ t = 3 hoặc t = x .

+ t = 3 ⇒ 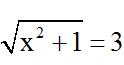⇔ x² = 8 ⇔ x = ±2√2 .

+ t = x ⇒ 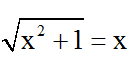⇒ x² + 1 = x². Phương trình vô nghiệm.

Vậy phương trình có hai nghiệm .

Bài tập trắc nghiệm tự luyện

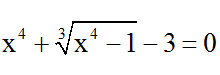
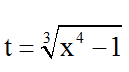
Bài 1: Cho phương trình: Nếu đặt thì t phải lưu ý điều kiện nào?

A. t ∈ R    B. t ≤ 1

C. t ≥ 1    D. t ≥ -1 .

Lời giải:

Đáp án: D

Bài 2: Số nghiệm của phương trình 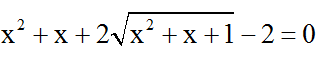là:

A. 0    B. 2    C. 4    D. 6

Lời giải:

Đáp án: B

Bài 3: Tập nghiệm của phương trình 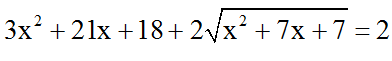có bao nhiêu phần tử?

A. 0    B. 2    C. 4    D. 6

Lời giải:

Đáp án: B

Bài 4: Cho phương trình 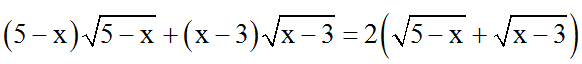Khẳng định nào dưới đây đúng?

A. Phương trình có nghiệm âm duy nhất.

B. Phương trình có 2 nghiệm trái dấu.

C. Phương trình có 2 nghiệm âm.

D. Phương trình có hai nghiệm dương.

Lời giải:

Đáp án: D

Bài 5: Phương trình 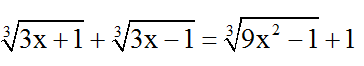có tổng các nghiệm bằng:

A. 3/2    B. 1    C. 2/3    D. -3/2 .

Lời giải:

Đáp án: C

Bài 6: Giải phương trình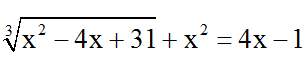

Hướng dẫn giải:

Ta có:

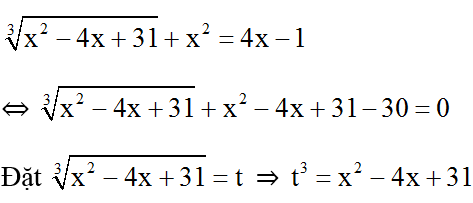
Phương trình trở thành: t + t³ - 30 = 0 ⇔ (t-3)(t² + 3t + 10) = 0 ⇔ t = 3

Thay trả lại biến x ta được:

⇔ x² - 4x + 31 = 27

⇔ x² - 4x + 4 = 0

⇔ (x-2)² = 0

⇔ x = 2.

Vậy phương trình có nghiệm x = 2.

Bài 7: Giải phương trình :

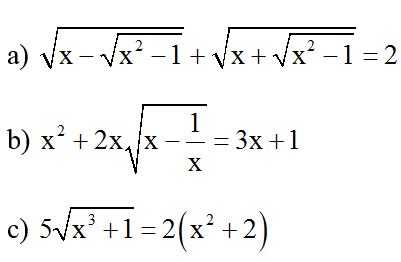
Hướng dẫn giải:

a) Đkxđ:

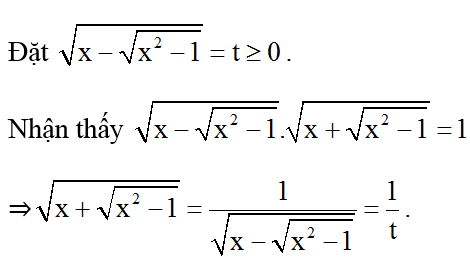
Phương trình trở thành:

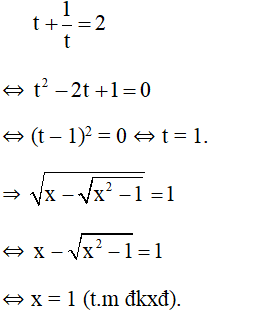
Vậy phương trình có nghiệm x = 1.

b) Đkxđ: x - 1/x ≥ 0 ; x ≠ 0 .

Chia cả hai vế của phương trình cho x ta được:

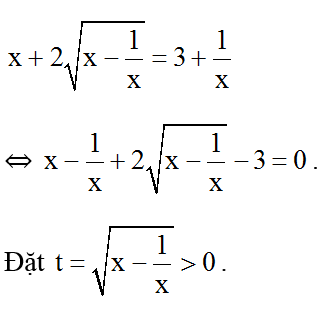
Pt trở thành: t² + 2t - 3 = 0 ⇔ (t + 3)(t – 1) = 0 ⇔ t = -3(L) hoặc t = 1 (t/m) .

+ t = 1

Vậy phương trình có hai nghiệm

c) Đkxđ: x ≥ -1 .

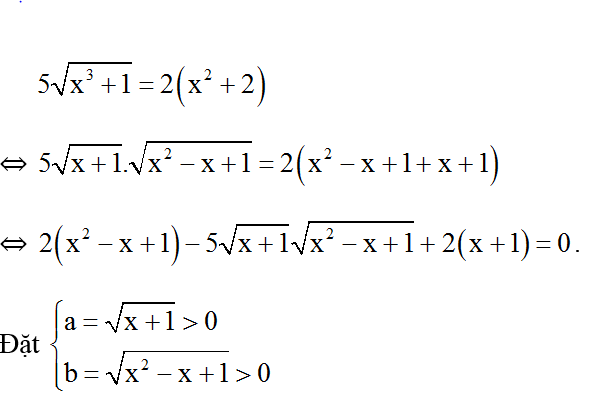
Phương trình trở thành : 2a² - 5ab + 2b² = 0

⇔ (2a-b) (a-2b) = 0

⇔ a = b/2 hoặc a = 2b

+ a = b/2 ⇔

⇔ x² - x + 1 = 4(x+1) ⇔ x² - 5x - 3 = 0 ⇔

+ a = 2b ⇔

⇔ x+1 = 4(x² - x + 1)⇔ 4x² -5x + 3 = 0

Phương trình vô nghiệm.

Vậy phương trình có hai nghiệm .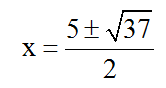

Bài 8: Giải phương trình:

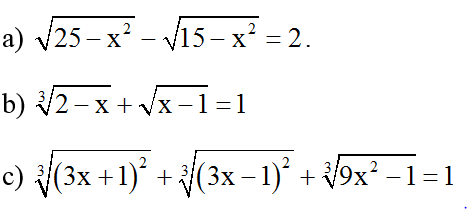
Hướng dẫn giải:

a) Đkxđ: x² ≤ 15.

Đặt

⇒ a² - b² = (25 - x²) - (15 - x²) = 10

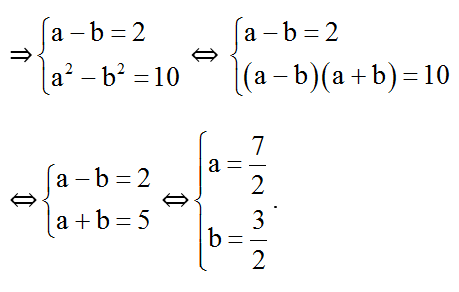
Thay trả lại biến x ta được:

Vậy phương trình có hai nghiệm

b)

Đkxđ: x ≥ 1.

Đặt

⇒ u³ + v² = 2 - x + x - 1 = 1(*)

Mà theo đề bài ta có u + v = 1 ⇒ v = 1 – u

Thay v = 1 – u vào (*) ta được: u³ + (1 – u)² = 1

⇔ u³ + u² – 2u + 1 = 1

⇔ u³ + u² – 2u = 0

⇔ u(u² + u – 2) = 0

⇔ u(u – 1)(u + 2) = 0

⇔ u = 0 hoặc u = 1 hoặc u = -2.

+ u = 0 ⇒ x = 2 (t.m)

+ u = 1 ⇒ x = 1 (t.m)

+ u = -2 ⇒ x = 10 (t.m)

Vậy phương trình có ba nghiệm x = 1; x = 2 và x = 10.

c)

Đkxđ: ∀x ∈ R.

Đặt

⇒ a³ - b³ = 2

⇒ (a – b)(a² + b² + ab) = 2 (*)

Phương trình trở thành: a² + b² + ab = 1 (**)

Thay vào (*) ta được: (a – b).1 = 2 ⇒ a – b = 2 ⇒ a = 2 + b

Thay a = 2 + b vào (**) ta được:

⇔ 3b² + 6b + 3 = 0

⇔ 3(b + 1)2 = 0

⇔ b = -1

⇒ ⇔ x = 0.

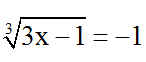
Thử lại x = 0 là nghiệm của phương trình.

Vậy phương trình có nghiệm x = 0.

Bài 9: Giải phương trình: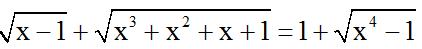

Hướng dẫn giải:

Đkxđ: x ≥ 1 .

Đặt

Khi đó

Phương trình trở thành:

a + b = 1 + ab ⇔ ab + 1 – a – b = 0 ⇔ (a – 1)(b – 1) = 0 ⇔ a = 1 hoặc b = 1

+ a = 1 ⇔ √(x-1) = 1 ⇔ x = 2.

+ b = 1 ⇔

⇔ x³ + x² + x = 0

⇔ x(x² + x + 1) = 0

⇔ x = 0 (không t.m đkxđ).

Vậy phương trình có nghiệm x = 2.

Bài 10: Giải phương trình: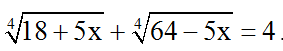

Hướng dẫn giải:

Đkxđ: -18/5 ≤ x > 64/5 .

Đặt

⇒ a⁴ + b⁴ = 18 - 5x + 64 + 5x = 82(*)

Phương trình trở thành: a + b = 4 (**)

⇒ a² + b² = (a+b)² - 2ab = 16 - 2ab

⇒ a⁴ + b⁴ = (a² + b²)² - 2a²b² = (16-2ab)² - 2a²b²= 2a²b² - 64ab + 256

Hay 2a²b² - 64ab + 256 = 82

⇔ a²b² - 64ab + 256 = 82

⇔ 2a²b² - 32ab + 87 = 0

⇔ (ab – 3)(ab – 29) = 0

⇔ ab = 3 hoặc ab = 29.

+ ab = 3.

Từ (**) ⇒ a = 4 – b.

Thay vào ab = 3 ⇒ (4 – b)b = 3 ⇔ b2 – 4b + 3 = 0 ⇔ (b – 1)(b – 3) = 0 ⇔

Nếu a = 3; b = 1 ⇒ ⇒ x =

Nếu a = 1; b = 3 ⇒ ⇒ x =

Thử lại cả hai đều là nghiệm của phương trình.

+ Nếu ab = 29

Từ (**)⇒ a = 4 – b.

Thay vào ab = 29 ⇒ (4 – b)b= 29 ⇔ b² – 4b + 29 = 0.

Phương trình vô nghiệm.

Vậy phương trình có hai nghiệm x = 63/5 và x = -17/5