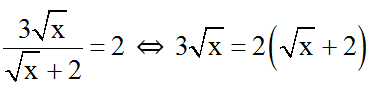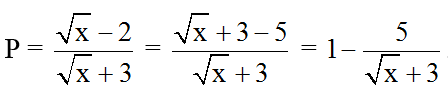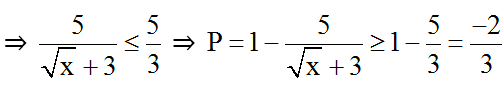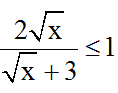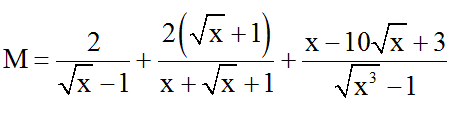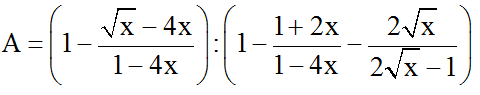Tìm giá trị của x để biểu thức có giá trị thỏa mãn đẳng thức, bất đẳng thức - Toán lớp 9

---

Tìm giá trị của x để biểu thức có giá trị thỏa mãn đẳng thức, bất đẳng thức

Với Tìm giá trị của x để biểu thức có giá trị thỏa mãn đẳng thức, bất đẳng thức Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Tìm giá trị của x để biểu thức có giá trị thỏa mãn đẳng thức, bất đẳng thức từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Phương pháp giải

a) Tìm điều kiện của x để biểu thức A < m (hoặc A > m ; A ≥ m; A ≤ m)

+ Tìm đkxđ

+ Rút gọn biểu thức (nếu cần)

+ Biến đổi điều kiện A < m để tìm ra x.

Lưu ý: Khi nhân (chia) cả 2 vế của BPT với một biểu thức dương thì chiều của BPT không đổi.

b) Tìm điều kiện của x để hàm số đạt GTLN, GTNN.

+ Tìm đkxđ

+ Rút gọn biểu thức (nếu cần).

+ Áp dụng các bất đẳng thức dể đánh giá biểu thức ≤ k (tìm GTLN) hoặc ≥ k (tìm GTNN) (k là hằng số)

+ Tìm x để dấu = xảy ra.

Lưu ý: Bất đẳng thức Cô-si: a² + b² ≥ 2ab

A² ≥ 0 với mọi A.

Ví dụ minh họa

Ví dụ 1: Tìm giá trị của x để biểu thức 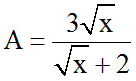có giá trị bằng 2.

Hướng dẫn giải:

Đkxđ: x ≥ 0.

Ta có:

3√x = 2√x + 4 ⇔ √x = 4 ⇔ x = 16.

Vậy x = 16.

Ví dụ 2: Cho biểu thức 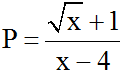Tìm x để 1/P ≤ -5/2.

Hướng dẫn giải:

Đkxđ: x ≥ 0; x ≠ 4 .

Ta có:

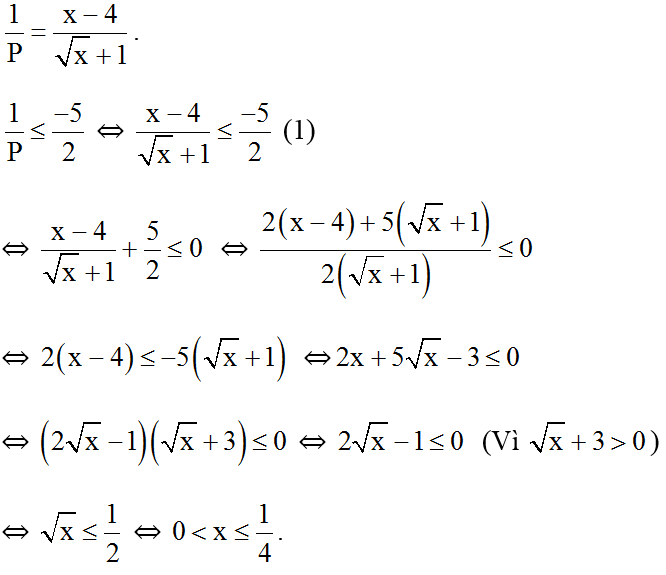
Vậy 0 < x < 1/4 .

Ví dụ 3: Cho biểu thức 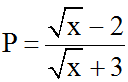Tìm x sao cho P đạt giá trị nhỏ nhất.

Hướng dẫn giải:

Ta có:

Với ∀x ∈ R: √x ≥ 0 ⇒ √x + 3 ≥ 3

Dấu “=” xảy ra khi x = 0.

Vậy Min_P = -2/3 khi x = 0.

Bài tập trắc nghiệm tự luyện

Bài 1: Biểu thức 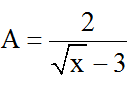có giá trị bằng 2 khi:

A. x = 4.     B. x = 2

C. x = 8     D. x = 16.

Lời giải:

Đáp án: D

Bài 2: Giá trị nào của x làm cho biểu thức 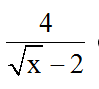có giá trị bằng -1.

A. x = 36     B. x = 4

C. x = 0     D. Đáp án khác.

Lời giải:

Đáp án: D

Bài 3: Giá trị nào của x dưới đây làm cho biểu thức .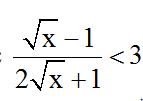

A. x < 9    B. x > 9.

C. Không có giá trị nào của x    D. Mọi x ∈ R.

Lời giải:

Đáp án: D

Bài 4: Có bao nhiêu giá trị nguyên của x thỏa mãn

A. 3    B. 9

C. 4    D. 10

Lời giải:

Đáp án: D

Bài 5: Giá trị nhỏ nhất của biểu thức 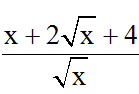là:

A. 4    B. 6

C. 8    D. 10

Lời giải:

Đáp án: B

Bài 6: Tìm giá trị của x để biểu thức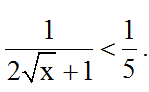

Hướng dẫn giải:

Đkxđ: x ≥ 0.

Ta có:

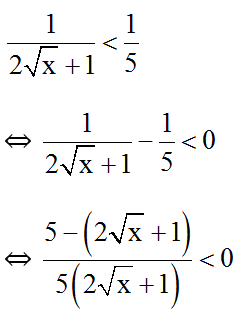
⇔ 4 -2√x < 0 ⇔ √x > 2 ⇔ x > 4 (t/m đkxđ).

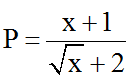
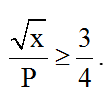
Bài 7: Cho . Tìm x để biểu thức

Hướng dẫn giải:

Đkxđ : x ≥ 0.

Ta có :

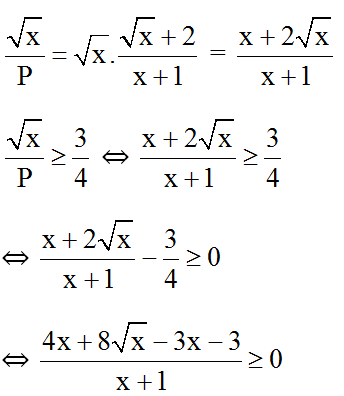
⇔ x + 8√x - 3 ≥ 0 (Vì x + 1 > 0)

⇔ (√x + 4)² ≥ 19

⇔ √x + 4 ≥ √19 (Vì √x + 4 > 0)

⇔ √x *ge; √19 - 4

⇔ x ≥ 35 - 8√19

Vậy x ≥ 35 - 8√19

Bài 8: Tìm x để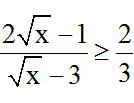

Hướng dẫn giải:

Đkxđ: x > 0; x ≠ 9 .

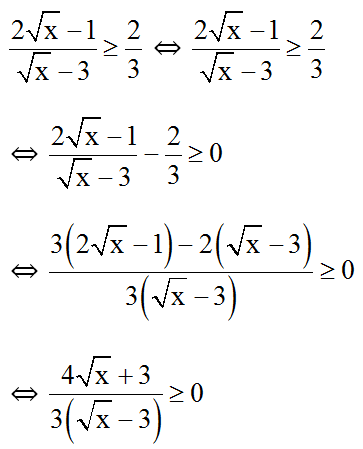
⇔ √x - 3 > 0

⇔ √x > 3

⇔ x > 9.

Vậy x > 9.

Bài 9: Cho biểu thức:

Tìm x để biểu thức có giá trị lớn nhất.

Hướng dẫn giải:

Đkxđ: x ≥ 0; x 1.

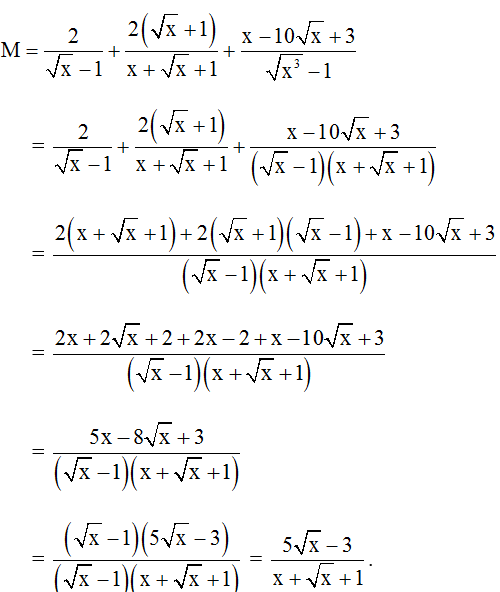
Ta có : (√x - 2)² ≥ 0 hay x - 4√x + 4 ≥ 0

⇒ x + √x + 1 - 5√x + 3 ≥ 0

⇒ x + √x + 1 ≥ 5√x - 3

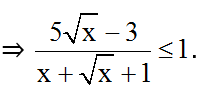
Dấu “=” khi √x = 2 ⇔ x = 4.

Vậy Max_M = 1 đạt được khi x = 4.

Bài 10: Cho

Tìm x để |A| ≤ 1/4 .

Hướng dẫn giải:

Đkxđ : x ≥ 0; x ≠ 1/4 .

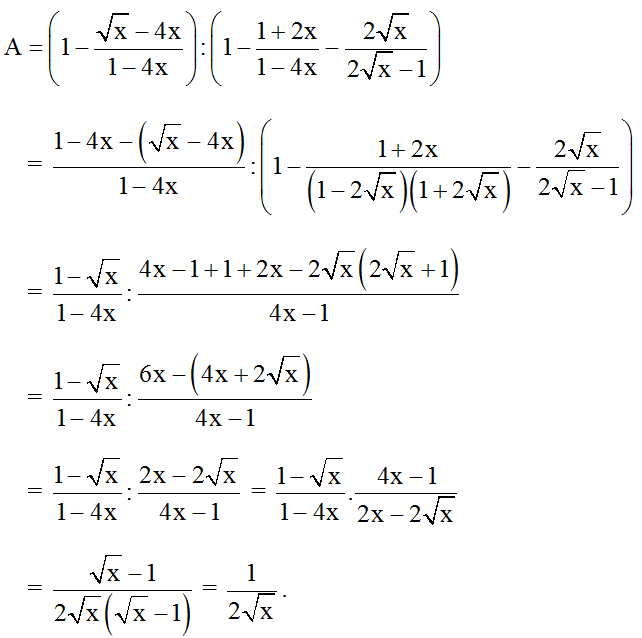
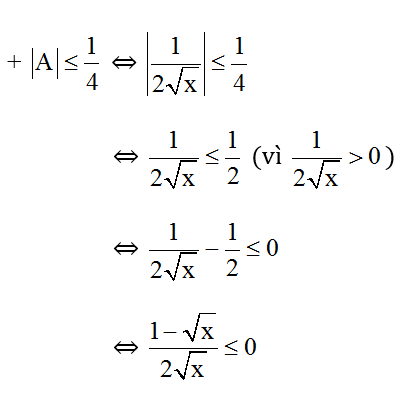
⇔ 1 - √x ≤ 0

⇔ √x ≥ 1

⇔ x ≥ 1 (t.m đkxđ)

Vậy với x ≥ 1 thì |A| ≤ 1/4 .