Đường tròn ngoại tiếp - Đường tròn nội tiếp - Toán lớp 9
Đường tròn ngoại tiếp - Đường tròn nội tiếp
Với Đường tròn ngoại tiếp - Đường tròn nội tiếp Toán lớp 9 gồm đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Đường tròn ngoại tiếp - Đường tròn nội tiếp từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

A. Phương pháp giải
1. Đường tròn đi qua tất cả các đỉnh của một đa giác được gọi là đường tròn ngoại tiếp đa giác và đa giác đó gọi là đa giác nội tiếp đường tròn.
2. Đường tròn tiếp xúc với tất cả các cạnh của một đa giác được gọi là đường tròn nội tiếp đa giác và đa giác được gọi là đa giác nội tiếp đường tròn.
3. Bất cứ đa giác đều nào cũng có một và chỉ một đường tròn ngoại tiếp, có một và chỉ một đường tròn nội tiếp.
Trong đa giác đều tâm của đường tròn ngoại tiếp trùng với tâm của đường tròn nội tiếp và được gọi là tâm của đa giác đều.
B. Bài tập tự luận
Bài 1: Nêu cách vẽ tam giác ABC đều nội tiếp đường tròn (O; R) cho trước. Tính cạnh của tam giác ABC theo R.
Hướng dẫn giải
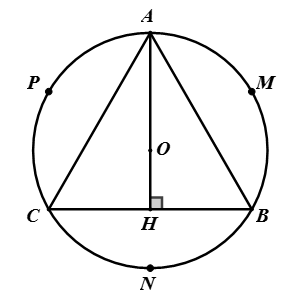
Cách vẽ:
Trên đường tròn (O; R) cho trước đặt liên tiếp các điểm A, M, B, N, C, P sao cho .
Nối AB, BC, CA ta được tam giác ABC đều nội tiếp đường tròn (O; R).
Thật vậy:
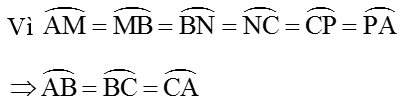
=> AB = BC = CA
Do đó tam giác ABC đều.
* Tính cạnh của tam giác ABC theo R.
Vì ΔABC đều có O là tâm đường tròn ngoại tiếp nên O cũng là trực tâm và trọng tâm của ΔABC
Nối AO cắt BC tại H ta có: OA = 2/3AH
Mà OA = R => AH = 3/2 R
Xét ΔABH vuông tại H nên:
AB2 = AH2 + BH2
⇔ AB2 = 3R2
⇔ AB = √3 R
Vậy cạnh của ΔABC là AB = BC = CA = √3R .

Bài 2: Cho đa giác đều n cạnh A1A2..An có O là tâm đường tròn ngoại tiếp đa giác đó và a là độ dài cạnh đa giác. Tính bán kính R, r của đường tròn ngoại tiếp, nội tiếp đa giác đó theo a và n.
Hướng dẫn giải
Vì A1A2..An là đa giác đều và O là tâm đường tròn ngoại tiếp đa giác nên O cũng là tâm đường tròn nội tiếp đa giác đó.
Nối OA1, OA2 và kẻ OH ⊥ A1A2 .
Xét ΔOA1H vuông tại H có:
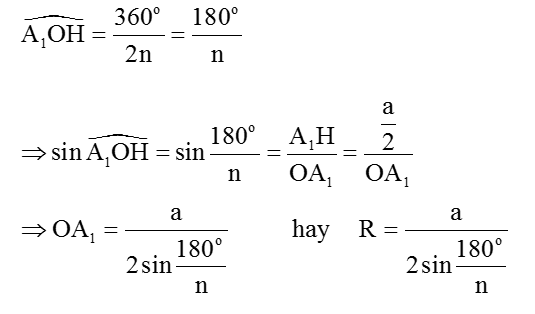
Lại có: OH = r là bán kính đường tròn nội tiếp đa giác và OH = A1H. cotg ∠A1OH = a/2 cotg (180o/n)
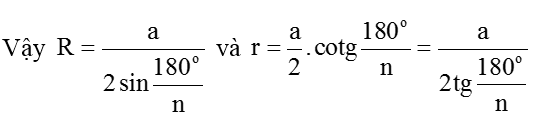
Bài 3: Chứng minh rằng với mọi đa giác đều có cùng số cạnh thì tỉ số giữa chu vi đa giác với đường kính của đường tròn ngoại tiếp không phụ thuộc độ dài của đường kính.
Hướng dẫn giải
Xét hai đa giác đều cạnh: A1A2..An có độ dài cạnh là a và bán kính đường tròn ngoại tiếp là R1
Đa giác đều B1B2..Bn có độ dài cạnh là b và bán kính đường tròn ngoại tiếp là R2
Theo ví dụ 2 ta có:
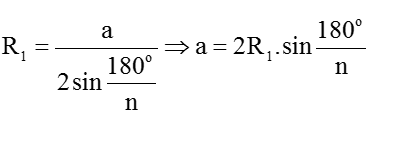
=> Chu vi đa giác A1A2..An là: p1 = n.a = 2R1.n.sin (180o/n)
Do đó p1 /2R1 = n.sin (180o/n) = p2 / 2R2
Vậy tỉ số giữa chu vi và độ dài đường kính của đường tròn ngoại tiếp một đa giác đều không phụ thuộc vào độ dài đường kính.
Bài 4: Trên đường tròn (O; R) lần lượt đặt theo cùng một chiều kẻ từ điểm A, cung AB = 45o , cung BC = 90o , cung CD = 45o .
a) Tứ giác ABCD là hình gì? Vì sao?
b) Tính chu vi và diện tích tứ giác ABCD theo R.
Hướng dẫn giải
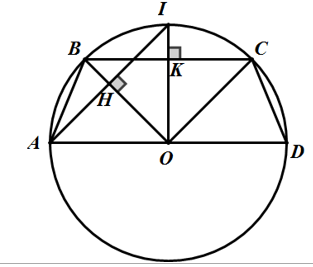
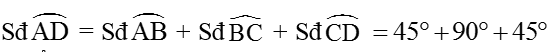
=> A, O, D thẳng hàng.
Vì Sđ BC = 90o suy ra ΔBOC vuông cân ở O nên: ∠OBC = 45o => ∠OBC = ∠BOA
Mà hai góc này ở vị trí so le trong, suy ra BC // AD (1)
Lại có: Sđ BD = Sđ AC = 90o + 45o = 135o (2)
Từ (1) và (2) suy ra tứ giác ABCD là hình thang cân.
b) Vì tam giác BOC vuông cân tại O nên: BC2 = OB2 + OC2 = 2R2
=> BC = √2R
Gọi I là điểm chính giữa của cung BC , nối AI cắt OB tại H.
Dễ thấy ΔAHO vuông cân tại H, có OA = R => AH = R√2/2 = HO
Do đó: BH = OB - OH = R - R√2/2 .
Xét ΔABH vuông tại H nên:
AB2 = AH2 + BH2
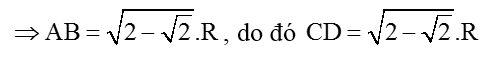
Vậy chu vi hình thang ABCD là:
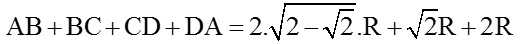
Dễ thấy: SΔABO = SΔCDO = R2√2 /4
SΔCBO = R2/2
Do đó diện tích của hình thang ABCD là: