Bài tập trắc nghiệm Hệ thức lượng trong tam giác vuông - Toán lớp 9

---

Bài tập trắc nghiệm Hệ thức lượng trong tam giác vuông

Với Bài tập trắc nghiệm Hệ thức lượng trong tam giác vuông Toán lớp 9 tổng hợp 14 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập Hệ thức lượng trong tam giác vuông từ đó đạt điểm cao trong bài thi môn Toán lớp 9.

Câu 1: Cho tam giác ABC vuông tại A có đường cao AH xuất phát từ A và AB=3; AC=4. Tính độ dài đoạn AH

A. 2,5 cm   B. 3cm   C. 2,4cm   D. 2cm

Câu 2: Cho tam giác ABC vuông tại A, có AB=9cm, AC=12cm. Độ dài đường cao AH là:

A. 7,2 cm   B. 5cm   C. 6,4 cm   D. 5,4cm

Câu 3: Cho tam giac ABC vuông tại A có AB=2cm, AC=4cm. Độ dài đường cao AH là:

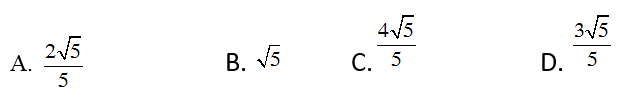
Câu 4: Tam giác ABC vuông tại A, có AB=2cm, AC=3cm. Khi đó độ dài đường cao AH bằng:

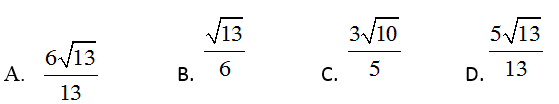
Câu 5: Cho tam giác ABC có AH là đường cao xuất phát từ A, hệ thức nào dưới đây chứng tỏ tam giác ABC vuông tại A

A. BC² = AB² + AC²

B. AH² = HB.HC

C. AB² = BH.BC

D. A, B, C đều đúng.

Câu 6: Cho tam giác ABC có đường cao xuất phát từ A. Nếu ∠BAC = 90^o thì hệ thức nào dưới đây đúng?

A. BC² = AB²+AC²

B. AH² = HB.HC

C. AB² = BH.BC

D. A, B, C đều đúng.

Câu 7: Cho tam giác ABC có và AH là đường cao xuất phát từ A. Câu nào sau đây là đúng?

Câu 8: Tam giác ABC vuông có đường cao AH( H thuộc cạnh BC). Hình chiếu của H trên AB là D, trên AC là E. Câu nào sau đây sai:

Câu 9: Cho tam giác ABC nội tiếp đường tròn đường kính BC=10cm. Cạnh AB=5cm, thì độ dài đường cao AH là:

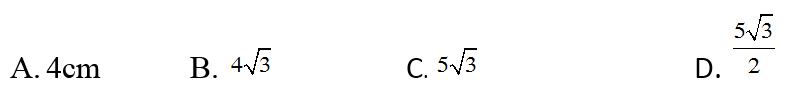
Hướng dẫn giải và đáp án

Câu 1: Áp dụng định lý py-ta-go vào tam giác vuông ABC có:

BC²=AB²+AC²

Thay số ta tính được BC=5.

Áp dụng hệ thức lượng vào tam giác ABC có: AH.BC = AB.AC

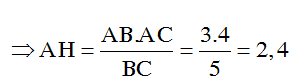
Vậy chọn đáp án:C

Câu 2: Chọn đáp án: A

Câu 3: Chọn đáp án: C

Câu 4: Chọn đáp án: A

Câu 5: Chọn đáp án: D

Câu 6: Chọn đáp án: D

Câu 7: Chọn đáp án: C vì ∠B + ∠C = 90^o suy ra tam giác ABC vuông tại A.

Câu 8: Chọn đáp án: D vì:

+ Đáp án A đúng vì AEHD là hình chữ nhật(vì có 3 góc vuông) nên 2 đường chéo AH và DE bằng nhau.

+ Xét tam giác ABC có :

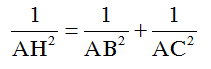
Vì AH = DE nên đáp án B đúng

Từ đó suy ra chọn đáp án D

Câu 9: Vì tam giác ABC nội tiếp đường tròn đường kính BC = 10cm nên tam giác ABC vuông tại A. Áp dụng định lý Py-ta-go ta có: AC² = BC² - AB².

Thay số vào ta tính được: AC= √75cm = 5√3 cm.

Áp dụng hệ thức lượng vào t tam giác vuông ABC có: AH.BC = AB.AC.

Thay số vào ta tính được: AH = 5√3/2 cm

Vậy chọn đáp án: D

Câu 10: Cho tam giác ABC vuông tại A, biết AB:AC=3:4, BC=15cm. Độ dài cạnh AB là:

A. 9cm   B. 10cm   C. 6cm   D. 3cm

Câu 11: Hình thang ABCD vuông góc ở A, D. Đường chéo BD vuông góc với cạnh bên BC biết AD=12cm, BC=20cm. Độ dài cạnh AB là:

A. 256/13cm   B. 9cm hay 16cm

C. 16cm   D. Một kết quả khác

Câu 12: Cho tam giác DEF vuông tại D, có DE=3cm, DF=4cm. Khi đó độ dài cạnh huyền bằng:

A. 5cm   B. 7cm   C. 6cm   D. 10cm

Câu 13: Cho tam giác ABC vuông tại A, đường cao AH. Biết AB=5cm, BC=13cm. Khi đó độ dài đoạn BH bằng:

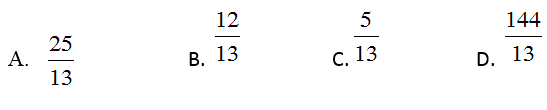
Câu 14: Tam giác ABC vuông tại A, đường cao AH. Biết AB=3cm, AC=4cm. Khi đó độ dài đoạn BH bằng:

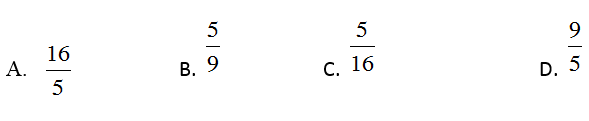
Hướng dẫn giải và đáp án

Câu 10: Gọi độ dài cạnh AB = 3x thì độ dài cạnh AC = 4x. Áp dụng định lý py-ta-go ta được:

⇔ 100 = 9x² + 16²

⇔ x² = 100 : 25

⇔ x = 2

Từ đó suy ra AB = 6cm

Câu 11: Kẻ BI ⊥ DC. Khi đó ABID là hình chữ nhật nên AD = BI; AB = DI = 12cm.

Xét tam giác vuông BIC có: IC²=BC²-BI²

Suy ra IC = 16cm.

Xét tam giác vuông BDC .Theo hệ thức lượng ta có: BI² = DI.IC

Thay số:16² = DI . 13.Tứ đó suy ra DI = 256/13 cm.

Vậy chọn đáp án A

Câu 12: Chọn đáp án: A

Câu 13: Áp dụng hệ thức lượng: AB² = BH.BC

Thay số ta được: 5²=BH.13.Suy ra BH = 25/13

Vậy chọn đáp án: A

Câu 14: Chọn đáp án: D